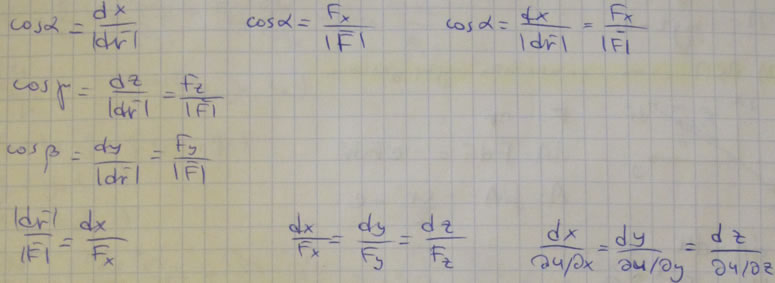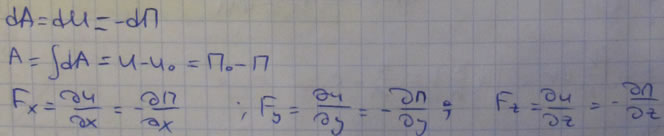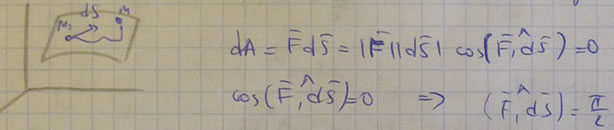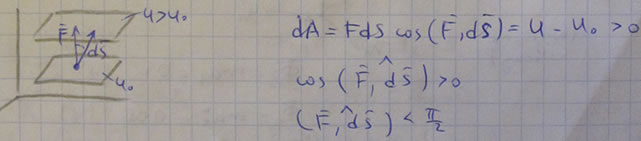потенциальное силовое поле это

Потенциальное силовое поле это

Потенциальное силовое поле. Силовая функция и потенциальная энергия поля. Поверхности уровня и их свойства.

Свойства поверхностей уровня.

Из лекций:

Силовым полем называют часть пространства в каждой точке которого на материальную точку действует сила зависящая от координат.

Например, в декартовой системе координат: U(x,y,z,t)

— потенциальное силовое поле

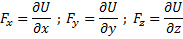
Вектор-градиент скалярной величины:

Основные свойства U стационарного потенциального силового поля.

Полная работа силы не зависит от пути перемещения.

Полная работа силы поля на каком-либо перемещении равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории (если силовая функция является однозначной) (при нестационарном поле это определение полной работы не действует).

Частный случай: Работа силы потенциального силового поля равна нулю, при перемещении точки по замкнутой траектории.

Потенциальной энергией (П) потенциального силового поля (ПСП) в заданной точке называется работа, которую совершают силы поля при перемещении материальной точки из данной точки в начальную.

Для всех точек U₀=const одинаковое.

Потенциальную энргию какой либо точки ПСП с точностью до константы можно определить как значение U в этой точке со знаком «минус» (-U).

Свойства поверхностей уровня:

1) Работа силы равна нулю, если начальные и конечные точки перемещения лежат на одном уровне.

2) Сила потенциального силового поля (ПСП) всегда перпендикулярна плоскости касательной к поверхности уровня.

3) Сила всегда направлена в сторону возрастания силовой функции.

4) Если поверхности уровня сближаются, то сила возрастает.

Источник

Потенциальное силовое поле

3.3.5.1. Потенциальное силовое поле и силовая функция

Силовое поле – это часть пространства, в каждой точке которого на материальную точку действует сила, зависящая от координат точки и времени (рис. 3.27)

Силовое поле называют стационарным, если силы не зависят явно от времени Если силы зависят от времени явно то поле – нестационарное.

Силовое поле называют потенциальным если имеется силовая функция частные производные которой по координатам равны проекциям силы на соответствующие координатные оси:

Рассмотрим основные свойства силовой функции стационарного поля.

1. Из определения следует, что силовая функция определена с точностью до постоянной

2. Элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции. Это свойство силовой функции можно принять за ее определение. Элементарная работа:

т.е.

3. Полная работа силы на каком–либо перемещении точки равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой совершается это перемещение, если силовая функция является однозначной (рис. 3.28). Полная работа силы на перемещении M₀M:

т.е.

4. Из предыдущего свойства следует, что работа силы в потенциальном силовом поле по любому замкнутому контуру равна нулю, так как значения силовой функции в начальной и конечной точках перемещения одинаковы:

5. Силу можно выразить как градиент силовой функции U. По определению:

т.е.

Определены условия, которые позволяют по силам силового поля установить, будет ли силовое поле потенциальным. Эти условия имеют вид:

Силы, действующие на материальную точку в потенциальном поле, называются потенциальными. К ним относят: силы тяжести, линейную силу упругости, силу тяготения.

Для механической системы в потенциальном силовом поле силовая функция является функцией координат всех точек системы

Проекция силы, действующей на каждую точку системы, будет равна

Если вычислить сумму работ, которую совершают силы поля, действующие на механическую систему при перемещении из положения (M₀), в котором силовая функция равна U₀, в положение (М), в котором силовая функция равна U, то получим

3.3.5.2. Потенциальная энергия

В случае потенциального силового поля вводят функцию, характеризующую запас энергии в данной точке поля – потенциальную энергию материальной точки в рассматриваемой точке силового поля.

Потенциальной энергией П материальной точки в рассматриваемой точке потенциального силового поля М (рис. 3.29) называют работу, которую совершают силы поля, действующие на материальную точку при перемещении ее из точки М в начальную точку M₀:

или где C=const.

Потенциальная энергия определена с точностью до постоянной

Проекции силы на координатные оси имеют вид:

Элементарная и полная работа силы в потенциальном силовом поле:

Потенциальной энергией системы P в рассматриваемом положении (М) потенциального силового поля называют сумму работ сил поля, действующих на систему, которую эти силы совершают при перемещении системы из рассматриваемого положения в начальное положение (M₀):

где U – значение силовой функции в положении (М); U₀ – значение силовой функции в начальном положении (M₀).

Проекции силы, действующей на каждую точку системы, на координатные оси имеют вид:

Элементарная и полная работа сил поля:

3.3.5.3. Закон сохранения механической энергии

Закон сохранения механической энергии точки. Для материальной точки, согласно теореме об изменении кинетической энергии, справедливо уравнение

Если точка движется в стационарном потенциальном силовом поле, то

или

Обозначая через Е полную механическую энергию точки, получаем

Закон сохранения механической энергии для точки. При движении точки в стационарном потенциальном силовом поле ее полная механическая энергия остается постоянной величиной.

Закон сохранения механической энергии системы. Теорему об изменении кинетической энергии для системы можно представить в виде

При движении системы в стационарном потенциальном силовом поле:

где П – потенциальная энергия внутренних и внешних сил, действующих на систему. Следовательно,

или

Последняя формула выражает закон сохранения механической энергии для системы.

Закон сохранения механической энергии для системы. Полная механическая энергия при движении системы в стационарном потенциальном силовом поле внешних и внутренних сил является величиной постоянной.

Механические системы, для которых выполняется закон сохранения механической энергии, называются консервативными.

Источник

Потенциальное силовое поле

Потенциальное силовое поле

Силовое поле М (х, у, z) Рисунок 72 Res Power Function U Если приложенное усилие не зависит от времени, считайте его стационарным. Если сила зависит от времени, силовое поле нестабильно. Если есть силовая функция U, силовое поле называется потенциальным. Это зависит от точечных и временных координат нестационарного силового поля. Цой проекция силы на координаты Ось для каждой точки в поле (рис. 72) имеет формулу Fx — dUldx–, Ff = dUISy, Fx = dU! определяется дз. (77) Функция U (x, y, z, t) называется силовой функцией. Рассмотрим основные характеристики силовой функции статического силового поля.

Задача о движении точек, притянутых к двум неподвижным центрам с силой, обратно пропорциональной квадрату расстояния, сначала сводится к основанному на Эйлере четырехугольнику для случая плоского движения. Людмила Фирмаль

Из (77) видно, что силовая функция точно определена для постоянной. Это связано с тем, что проекция силы на координатную ось требует только частичного дифференцирования по координатам этой функции, а добавление константы в функцию U не влияет на значения Fx, Fy и Ft. dH = Fdx + Rdy + Fzdz = ^ dx + ^ dy + ^ dz = dl /, ’Bh By Bz Это д / л = д <7. (78) Следовательно, основная работа силы в поле потенциальной силы равна полной производной от функции силы. Это свойство степенной функции может быть использовано для определения. (77) взято из (78).

Если область, окруженная закрытой пешеходной дорожкой, содержит специальные специальные точки функции мощности, функция мощности может принимать другие значения после возврата к исходной точке, в зависимости от количества прогулок. Я могу Применение концепции вектора градиента из скалярной функции U Где i, j и Jc — единичные векторы, ориентированные вдоль координатных осей, а сила F может быть выражена как градиент силовой функции V: F = градус U Определяет условия, при которых силовое поле может быть установлено, является ли оно силовым.

Если существует силовая функция U, dFx / dy = d2Uj (dy5х); dFy / dx = d2U / (dxdy). с того времени d2U! (8y dx) = d2 U / (dx dy), тогда dFxldy = dFyjdx или dFJdy — dFyldx = 0. Как хорошо dPr / dy — dFy ldz = 0 \ dFx / dz — 8F2 / 8x — 0 Следовательно, формат полученного условия ^ 5iao; S-Cp.o. (SO) ду дг дх дх ду ду В векторных вычислениях не только необходимо условие (80), но оно оказалось достаточным для существования силовых функций. При использовании вихревого вектора rot / 7 вектора силы F Условие (80) может быть выражено более легко. rotF = 0. (80) Следовательно, необходимо и достаточно, чтобы силовое поле не вращалось для потенциала. Непотенциальные силы — это сопротивление и трение в зависимости от скорости.

Сила трения постоянна независимо от скорости, но направление силы трения зависит от скорости, поэтому сила сухого трения не является потенциальной. Уровень поверхности. Линия электропередачи Учитывая точки потенциального силового поля, где силовая функция имеет одинаковое значение, например, U — C, все точки зажима находятся на поверхности. Это называется ровной поверхностью или ровной поверхностью. Форма уравнения поверхности уровня U (x, y, z) = C. Обратите внимание на некоторые свойства поверхности уровня. 1.

Возьмем две почти бесконечные точки M. и M t и вычислим основную задачу перемещения djj между этими точками. d4 = Fds1cos (F, L / L? 1). С другой стороны, с! Λ = 0. Следовательно, cos (F, MM2)> 0, поэтому мы видим, что угол 180 ° исключен и сила F направлена ​​вдоль MM2 в направлении увеличения значений функции силы. 4. Для первой поверхности с уровнем Ct = C / n, со второй поверхностью C2 = 2С / п и последней С = иС / и = С все силовое поле равно и равно уровню Если разделены, смежные поверхности На уровнях, близких друг к другу, коэффициент силы F равен Место, где горизонтальная плоскость находится дальше.

В этом случае, если вы заметили, что работа между точками на двух смежных поверхностях одинакова, вы можете проверить это свойство. Так где Расстояние между поверхностями будет короче, интенсивность чисел будет больше, и наоборот. Понятие силовых линий вводится вдоль горизонтальной плоскости в силовом поле. То есть линия каждой точки, где сила касается этой линии (рис. 74). Вектор dr, спроецированный на оси dx, dy, dz, всегда направлен вдоль тангенса кривой, поэтому из параллельных условий dr и F: dx / Fx = dylF, = dz / Ft. (81) Эти дифференциальные уравнения для координат x, y, z являются дифференциальными уравнениями для линий магнитного поля.

Наиболее распространенным способом построения уравнений в задаче, в которой определяется закон сил реакции или движения связей, является использование дифференциальных уравнений для плоского движения твердых тел. Людмила Фирмаль

Потенциальная энергия Рисунок 75 Для потенциальных силовых полей, в дополнение к силовой функции, вы можете ввести еще одну функцию, которая характеризует запас энергии в определенной точке поля. Это потенциальная энергия в этой точке (рис. 75) или потенциальная энергия в материальной точке в рассматриваемой точке силового поля. Потенциальная энергия P материальной точки в точке рассматриваемого силового поля M является работой, выполняемой силой поля, действующей на материальную точку при перемещении материальной точки из точки M в начальную точку Mo. P = AMMe или П = Aмм „= и0-и = С0-и. (82).

Константа Co одинакова для всех точек в поле, в зависимости от того, какая точка в поле выбрана в качестве первой точки. Очевидно, что потенциальная энергия может быть введена только для потенциальных силовых полей. В потенциальном поле работа не зависит от формы смещения между точками M и L / o. Непотенциальное силовое поле не имеет потенциальной энергии, поэтому нет силовой функции. На основании (77) и (82) вы можете: п-д. = dJL- p = ^ L = —dJL x dh dh ‘u do du’ z dz dz ‘ Получите поле (83) FORCE FL-FORCE мощность и давление Рис. 76.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Потенциальное силовое поле это

Лекция 9

Потенциальное силовое поле.
Определение и свойства потенциального силового поля.

Силовым полем называется трехмерное пространство, в каждой точке которого задана функция силы F(r;t). Если время t отсутствует явно, то поле стационарное.

Рассмотрим стационарное силовое поле, заданное в декартовых координатах x, y, z функциями:

Как было показано, для вычисления конечной работы силы силового поля, необходимо знать траекторию точки. Среди силовых полей существует класс потенциальных силовых полей, для которых конечная работа силы определяется только начальным и конечным положением точки и не зависит от траектории.

Силовое поле (38) называется потенциальным, если существует такая функция потенциальной энергии П(x,y,z), что

Пусть задано поле (*). Как проверить, является ли оно потенциальным? Мы считаем, что потенциальная энергия П является непрерывной, дважды дифференцируемой функцией координат. Тогда можно воспользоваться свойством: порядок взятия смешанной производной не влияет на результат :

, , ,

Отсюда критерии потенциальности cилового поля

Отсюда вытекают следующие свойства.

Поверхность на которой П сохраняет значение называется эквипотенциальной:

Поскольку dr направлено произвольно в касательной плоскости к поверхности П = С₁, то сила направлена перпендикулярно эквипотенциальным поверхностям.

F=

Значит, сила направлена в сторону убывания П.

По свойствам дифференцирования обе функции П(х,у,z) и П(х,у,z) + С, где С- произвольная аддитивная постоянная, определяют одно и тоже силовое поле. Говорят, что потенциальная энергия определена с точностью до постоянной.

Выберем нулевой уровень потенциальной энергии. Переместим точку из произвольного положения М(х,у,z) пространства в любую точку нулевого уровня и сосчитаем работу силы:

Отсюда правило вычисления функций потенциальной энергии:

Функция П(х,у,z) вычисляется как работа потенциальной силы

на перемещение из произвольной точки М(х,у,z) на нулевой уровень.

Направим ось вертикально вверх, тогда

Все поверхности z = const эквипотенциальны. Поэтому

Работа положительна, если точка опускается.

Прямая линейная пружина:

Пружина линейна, если сила F_в линейно зависит от деформации:

Коэффициент с (н/м) называется жесткостью пружины. Если начало оси х выбрать в положении, где Δ=0, то

Квадраты координат можно заменить их модулями- деформациями:

При закручивании пружины на угол φ, называемый деформацией пружины Δ’, возникает упругий восстанавливающий момент М_в. Пружина линейна, если

Коэффициент с’ (нм) называется жесткостью пружины.

A₁₂=
Система называется консервативной, если все действующие на неё силы потенциальны.

Теорема об изменении кинетической энергии для консервативной системы в интегральной форме:

Полной механической энергией системы называется сумма её кинетической и потенциальной энергий:

Как видим, полная механическая энергия консервативной системы сохраняется

Предположим, что кроме потенциальных сил, на систему действуют не потенциальные силы, тогда:

Поделив на dt, найдем, что скорость изменения полной механической энергии равна мощности непотенциальных сил.

Например, при наличии силы вязкого сопротивления

полная механическая энергия убывает со скоростью

Статический принцип возможных перемещений для консервативной системы.

Рассмотрим консервативную несвободную систему с потенциальной энергией П (x,y,z), и обобщенными координатами q₁. q_l. Найдем обобщенные силы системы по определению

Пример: эллиптический маятник

Примем за нулевой уровень потенциальной энергии положение x=0, φ=0 и вычислим работу при возвращении системы в начало координат

П не зависит от х, значит Q_x=0

Поскольку обобщенные возможные перемещения δq_i независимы, то принцип можно прочитать следующим образом:

В положении равновесия все обобщенные силы обращаются в ноль.

В положении равновесия потенциальная энергия консервативной системы имеет экстремум

Следовательно, нахождение положений равновесия консервативной системы сводится к нахождению экстремумов функции П.
Уравнение Лагранжа для консервативных систем.

Циклические координаты и интегралы.

Рассмотрим консервативную несвободную систему с l степенями свободы. Потенциальная энергия П(q₁. q_l) определяет обобщенные силы

Уравнения Лагранжа приобретают вид

(i=1,2. l)

Здесь учтено, что потенциальная энергия не зависит от обобщенных скоростей

Запишем уравнения Лагранжа через функцию Лагранжа

(i=1,2. l)

Координата q_σ называется циклической, если от нее не зависит функция Лагранжа

Уравнение Лагранжа с номером σ приобретает вид

и имеет циклический интеграл

Часто этот интеграл описывает случай сохранения количества движения или кинетического момента.

Пример: эллиптический маятник

П и Т не зависят от х, значит х- циклическая координата, и существует интеграл

Мы уже отмечали, что этот интеграл выражает ожидаемое сохранение количества движения системы вдоль оси х.

Актеры не уходят на покой. Просто они получают все меньшие и меньшие роли. Дэвид Нивен, по канве изрече
ещё >>

Источник