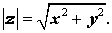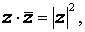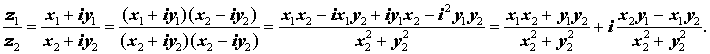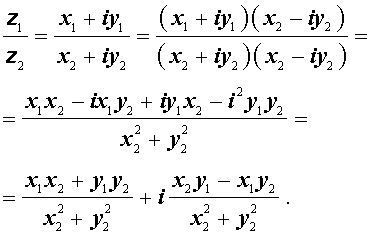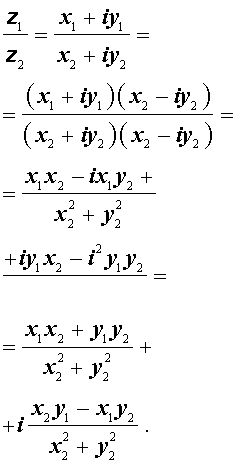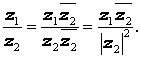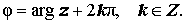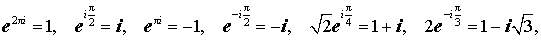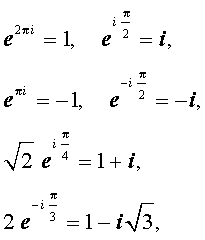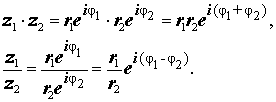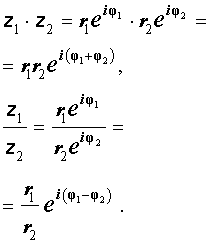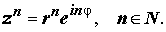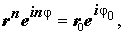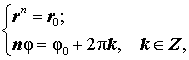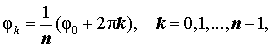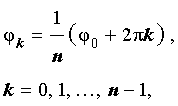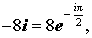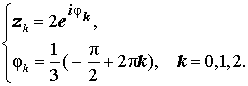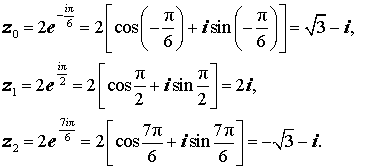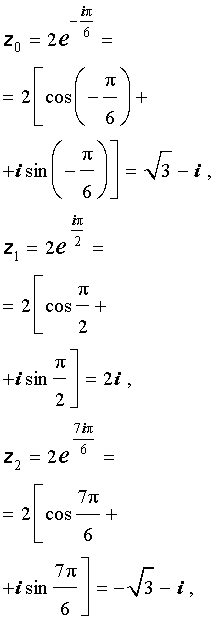поле комплексных чисел доказательство
Поле комплексных чисел
Рассмотрим важнейший пример числового поля — поле комплексных чисел.
Два комплексных числа и называются равными, если равны их действительные и мнимые части соответственно:
Сложение и вычитание в поле комплексных чисел
Суммой комплексных чисел и называется комплексное число
Из этого определения и свойств операции сложения действительных чисел следует, что:
а) операция сложения комплексных чисел коммутативна: ;
б) операция сложения комплексных чисел ассоциативна: ;
в) существует нулевой элемент ; нулевой элемент обозначается просто символом нуль ;
г) для каждого комплексного числа существует противоположный ему элемент
Из последнего свойства следует, что на множестве комплексных чисел определена операция вычитания (обратная к сложению). Разностью чисел и называется комплексное число
Умножение и деление в поле комплексных чисел
Произведением комплексных чисел и называется комплексное число
Из определения (В.6) и свойств операции умножения действительных чисел следует, что:
в) существует единичный элемент ; единичный элемент обозначается просто символом единица: ;
Из последнего свойства следует, что на множестве отличных от нуля комплексных чисел определена операция деления (обратная к умножению).
Частным двух чисел и называется комплексное число
Операции сложения и умножения комплексных чисел связаны законом дистрибутивности:
Таким образом, множество комплексных чисел является полем.
Решение. По определению операций получаем
Сопряженные числа в поле комплексных чисел
Из определения следует, что сумма и произведение сопряженных чисел — есть числа действительные:
Используя правила арифметических операций для комплексных чисел, можно установить справедливость свойств операции комплексного сопряжения:
Решение. Пусть — корень уравнения. Тогда
Приравнивая нулю действительную и мнимую части, получаем
3. Из свойств операции комплексного сопряжения следует, что
Поле комплексных чисел



Теорема 1. Множество комплексных чисел С с операциями сложения и умножения образует поле. Свойства сложения
1) Коммутативность:(a+bi)+(c+di)=(a+c)+(b+d)i=(c+di)+(a+bi).
2) Ассоциативность :[(a+bi)+(c+di)]+(e+fi)=(a+c+e)+(b+d+f)i=(a+bi)+[(c+di)+(e+fi)].
3) Существование нейтрального элемента:(a+bi)+(0+0i)=(a+bi). Число 0+0i будем называть нулём и обозначать 0.
4) Существование противоположного элемента: (a+bi)+(–a–bi)=0+0i=0.
5) Коммутативность умножения: (a+bi)(c+di)=(ac–bd)+(bc+ad)i=(c+di)(a+bi).
6) Ассоциативность умножения:если z1=a+bi, z2=c+di, z3=e+fi, то (z1z2)z3 =z1(z2z3).
7) Дистрибутивность: если z1=a+bi, z2=c+di, z3=e+fi, то z1(z2+z3)=z1z2+z1z3.
8) Нейтральный элемент для умножения:(a+bi)(1+0i)=(a·1–b·0)+(a·0+b·1)i=a+bi.
9) Число 1+0i=1 – единица.
Если b=0, то z=a+ 0i=a– действительное число. Поэтому множество действительных чисел Rявляется частью множества комплексных чисел C: R Í C.
Заметим: i 2 =(0+1i)(0+1i)=–1+0i=–1. Используя это свойство числа i, а также свойства операций, доказанные в теореме 1, можно выполнять действия с комплексными числами по обычным правилам, заменяя i 2 на –1.
2 Тригонометрическая форма записи.



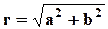
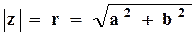
Полярный угол j называется аргументом числа z: 
Аргумент определяется с точностью до слагаемого 2kp; значение, для которого –p
Поле комплексных чисел доказательство
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число 
где r =| z | — модуль комплексного числа, а угол 
Пример 7.1. Записать комплексные числа 
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Поле комплексных чисел доказательство
VII .1. Формы записи комплексных чисел и действия над ними
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число 
где r =| z | — модуль комплексного числа, а угол 
Пример 7.1. Записать комплексные числа 
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Комплексные числа
 Алгебраическая форма записи комплексных чисел Алгебраическая форма записи комплексных чисел |
 Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
 Комплексно сопряженные числа Комплексно сопряженные числа |
 Модуль комплексного числа Модуль комплексного числа |
 Деление комплексных чисел, записанных в алгебраической форме Деление комплексных чисел, записанных в алгебраической форме |
 Изображение комплексных чисел радиус-векторами на координатной плоскости Изображение комплексных чисел радиус-векторами на координатной плоскости |
 Аргумент комплексного числа Аргумент комплексного числа |
 Тригонометрическая форма записи комплексного числа Тригонометрическая форма записи комплексного числа |
 Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера. Экспоненциальная форма записи комплексного числа |
 Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
 Извлечение корня натуральной степени из комплексного числа Извлечение корня натуральной степени из комплексного числа |
Алгебраическая форма записи комплексных чисел
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Комплексно сопряженные числа
 | 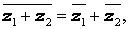 |
 | 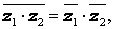 |
 | 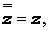 |
 | 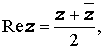 |
 | 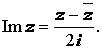 |
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
 | 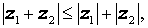 |
 | 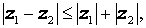 |
 | 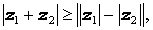 |
 | 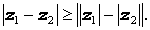 |
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
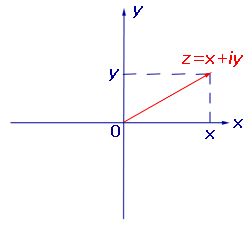
Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
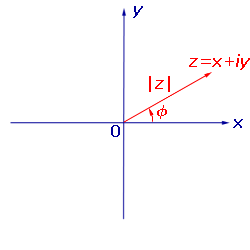
Аргумент комплексного числа
Считается, что комплексное число нуль аргумента не имеет.
Тогда оказывается справедливым равенство:
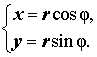 | (3) |
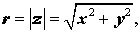 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | 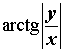 | 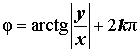 | 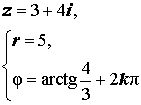 | |
| Положительная мнимая полуось | 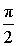 | 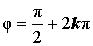 | 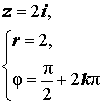 | |
| Второй квадрант | 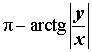 | 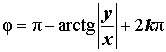 | 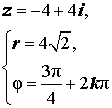 | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры | 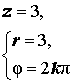 |
значение
аргумента
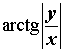
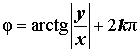
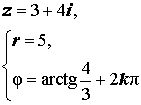
значение
аргумента
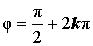
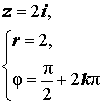
значение
аргумента
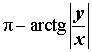
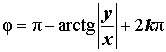
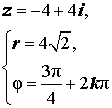
x z
квадрант
x z
мнимая
полуось
y z
квадрант
Положительная вещественная полуось
Главное значение аргумента:
Расположение числа z :
Главное значение аргумента:
Расположение числа z :
Положительная мнимая полуось
Главное значение аргумента:
Расположение числа z :
Главное значение аргумента:
Расположение числа z :
Отрицательная вещественная полуось
Отрицательная мнимая полуось
x z = x + i y может быть записано в виде
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 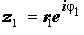
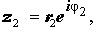
Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Извлечение корня натуральной степени из комплексного числа
Пусть 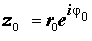
Для того, чтобы решить уравнение (8), перепишем его в виде
следствием которых являются равенства
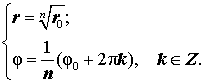 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
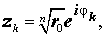 | (10) |
то по формуле (10) получаем: