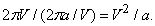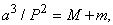Небесная динамика что изучает

Новое в блогах

Небесная механика

Небесная механика — это раздел астрономии, который изучает движение небесных тел, кос­мических аппаратов, искусственных и естественных спутни­ков планет под действием сил гравитации.

Задачей небесной механики является предсказание положений небесных тел, ис­следование устойчивости Солнечной системы и звёздных сис­тем, определение значений астрономических постоянных, по­строение теории движения тел Солнечной системы с учётом эффектов общей теории относительности. В ряде случаев учи­тывается давление света (в движении комет и астероидов), си­лы сопротивления среды (в движении ИСЗ), изменение массы и другие факторы. Для особо точных расчётов длительных ко­смических полётов и движения астероидов учитываются по­правки за счёт современной теории пространства-времени-тяготения — общей теории относительности.

Возникновение

Огромное значение для развития астрономии имели откры­тия гениального английского учёного И. Ньютона. Используя сформулированные им законы движения (законы Ньютона), он показал, что законы Кеплера следуют из законов движения, если силы, действующие между телами, изменяются обратно про­порционально квадратам рассто­яний между ними, т. е. открыл закон всемирного тяготения.

Пользуясь законами, открытыми Ньютоном и разработанными им же новыми математическими ме­тодами, учёные смогли создать теорию движения планет. Это привело к тому, что в астроно­мии выделились два раздела: астрометрия и небесная механи­ка (подобно тому, как в физике в своё время выделились меха­ника, оптика, электродинамика и др.), которые бурно развивались в XVII—XIX вв.

Развитие

Первый значительный успех небесной механики был свя­зан с кометами. Кометы — «хвостатые звезды», названные так за необычный вид. Они внезапно появляются на небе, быстро проносятся среди звёзд и исчезают. В 1705 г. Э. Галлей предположил, что три кометы, наблюдавшиеся в 1531, 1607 и 1682 гг., являются одним и тем же небесным телом, двигающимся по эллиптической орбите с периодом око­ло 76 лет, и предсказал новое появление кометы в 1858 г. Ор­биту кометы уточнил А. Клеро, и она появилась в назначен­ное время. Эта комета получила название кометы Галлея. По­следний раз она появилась в 1986 г.

К 40-м гг. XIX в. стало ясно, что движение открытого Гер­шелем Урана нельзя объяснить притяжением Солнца и изве­стных к тому времени планет. Была выдвинута гипотеза о су­ществовании ещё одной планеты Солнечной системы.

Эта планета Нептун была открыта 23 сентября 1946 г. не­мецким астрономом И. Галле по вычислениям У. Леверье. От­крытие Нептуна окончательно доказало правильность ньюто­новской теории тяготения.

Величайшим триумфом небесной механики ознаменовались полёты космических советских станций «Вега-1» и «Вега-2» к комете Галлея в 1975—1976 гг. и американских «Вояд­жер-1» и «Вояджер-2» к Юпитеру, Сатурну, Урану и Непту­ну в 1977—1989 гг. Эти полёты продолжаются и в настоящее время. Материал с сайта http://wikiwhat.ru

Задачи небесной механики

Основная задача небесной механики заключается в расчёте движения небесных тел под действием сил всемирного тяготения. В эту задачу включают исследование и расчёт движения планет, искусст­венных спутников Земли (ИСЗ), космических аппаратов, звёзд в двойных и кратных системах, строения галактик. Среди них наиболее популярной и классической является задача n тел.

В число задач небесной механики включают и учёт приливных сил, возникающих вследствие неоднородности поля тяготения.

Все эти задачи в математическом смысле исключительно трудны. Большинство из них решается численными методами с использованием самых мощных компьютеров. Но есть и задачи, ко­торые могут быть решены в аналитическом виде.

Источник

Динамика небесных сфер

СОДЕРЖАНИЕ

Небесный материал и его естественные движения [ править ]

Причины небесного движения [ править ]

Более поздние греческие переводчики [ править ]

Исламские переводчики [ править ]

Исламские философы аль-Фараби (ок. 872–950) и Авиценна (ок. 980–1037), вслед за Плотином, утверждали, что движущие силы Аристотеля, называемые разумными существами, возникли в результате серии эманаций, начиная с Бога. Первый разум исходил от Бога, а из первого разума возникла сфера, его душа и второй разум. Процесс продолжался через небесные сферы до сферы Луны, ее души и окончательного разума. Они считали, что каждая сфера постоянно движется своей душой, стремясь подражать совершенству ее разума. [30] [31] Авиценна утверждал, что, помимо разума и его души, каждая сфера также была перемещена естественной склонностью (Майл ). [32]

Более влиятельными для более поздних христианских мыслителей были учения Аверроэса (1126–1198), который согласился с Авиценной в том, что разум и души объединяются для перемещения сфер, но отверг его концепцию эманации. [31] [36] Учитывая, как действует душа, он утверждал, что душа перемещает свою сферу без усилий, поскольку небесный материал не имеет тенденции к противоположному движению. [37]

Средневековая Западная Европа [ править ]

В двух немного разных обсуждениях Джон Буридан (1295–1358 гг.) Предположил, что, когда Бог создал небесные сферы, он начал их перемещать, внося в них круговой импульс, который не был бы ни искажен, ни уменьшен, поскольку не было ни наклонности. другим движениям и никакому сопротивлению в небесной области. Он отметил, что это позволит Богу отдохнуть в седьмой день, но оставил этот вопрос на усмотрение богословов. [52] [53] [54]

Двигатели и коперниканство [ править ]

Хотя Николай Коперник (1473–1543) преобразовал птолемеевскую астрономию и аристотелевскую космологию, переместив Землю из центра Вселенной, он сохранил как традиционную модель небесных сфер, так и средневековые аристотелевские взгляды на причины ее движения. Коперник следует Аристотелю, утверждая, что круговое движение естественно для формы шара. Однако он также, похоже, принял традиционное философское убеждение, что сферы перемещаются внешним движителем. [61]

Космология Иоганна Кеплера (1571–1630) исключила небесные сферы, но он считал, что планеты движутся как внешней движущей силой, которую он разместил на Солнце, так и движущей силой души, связанной с каждой планетой. В ранней рукописи, в которой обсуждается движение Марса, Кеплер считал, что Солнце вызывает круговое движение планеты. Затем он приписал движение планеты внутрь и наружу, которое преобразует ее общее движение из кругового в овальное, к движущейся душе на планете, поскольку движение является «не естественным движением, а скорее одушевленным». [62] В различных работах Кеплер часто приписывал врожденные двигательные способности, связанные со звездами, своего рода интеллект. [63]

После Коперниканизма планеты стали рассматриваться как тела, свободно движущиеся в очень тонкой эфирной среде. Хотя многие схоласты продолжали утверждать, что небесными движителями были разумные существа, теперь они связывали разумные существа с самими планетами, а не с небесными сферами. [64]

Источник

Небесная динамика что изучает

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.

Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Глава I

ФИЗИЧЕСКИЕ ОСНОВЫ ТЕОРИЙ ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ

1. Краткий очерк развития небесной механики и
звездной динамики

Небесная механика зародилась в глубокой древности, когда получила распространение астрология. Для того, чтобы составить астрологические прогнозы (гороскопы), нужно было знать расположение зодиака относительно горизонта, а также положения планет, что привело к уточнению периодов движения планет и созданию первых, хотя и очень несовершенных, теорий движения планет. Уже греческий астроном Аристарх Самосский в 3-ем веке до н.э. высказывал мысль, что Земля движется вокруг Солнца, а Гераклит еще раньше предполагал, что Земля вращается вокруг оси.

Современник Г. Галилея И. Кеплер на основе наблюдений движения планет, выполненных его учителем Тихо Браге, установил три закона движения планет. Первый закон: планеты движутся по эллипсам, в фокусе которых находится Солнце. Второй закон определяет зависимость скорости движения планеты от ее положения на орбите. Третий закон устанавливает связь между размерами орбиты планеты и ее периодом обращения вокруг Солнца. В реальности, при взаимном притяжении между всеми телами Солнечной системы, движение планет сложнее, чем законы Кеплера.

Гюйгенс (1629-1695 г.г.) в работе «Система Сатурна» (1659 г.) установил, что Сатурн окружен тонким кольцом, состоящим из малых тел, нигде не примыкающим к планете и наклоненным к плоскости эклиптики, открыл спутник Сатурна Титан, дал первое описание туманности в созвездии Ориона. Гюйгенс близко подошел к открытию закона всемирного тяготения (приложение «О причинах тяжести» в «Трактате о свете»).

Ж.Пикар (1620-1682 г.г.) в 1669-70 г.г. измерил дугу меридиана, получив данные о размерах Земли, которые в дальнейшем были использованы для численного подтверждения закона всемирного тяготения.

Силы тяготения (гравитационные поля) отдельных тел обладают свойством аддитивности, то есть сила, действующая на некоторое тело со стороны нескольких других тел, равна геометрической сумме сил, действующих на тело со стороны каждого тела. Из этого следует, что однородное шарообразное тело притягивает другие тела так же, как материальная точка, если расстояние измерять от центра шара.

Исходя из установленных эмпирическим путем И. Кеплером законов движения планет астроном И. Бульо, физики Дж. Борелли и Р. Гук высказали соображения, что орбитальное движение планет может быть объяснено действием силы, которая притягивает каждую планету к Солнцу и которая убывает пропорционально квадрату расстояния от Солнца. Однако только И. Ньютон в «Математических началах натуральной философии» (1687 г.) впервые это строго доказал, исходя из своих первых двух законов механики. И. Ньютон доказал, что орбитальное движение каждой планеты должно подчиняться первым двум законам Кеплера именно в том случае, если они движутся под действием силы тяготения Солнца. Далее Ньютон доказал, что орбитальное движение Луны может быть объяснено приблизительно с помощью аналогичного силового гравитационного поля Земли и что сила тяжести на Земле есть результат воздействия того же силового поля на материальные тела.

Гравитационное взаимодействие в соответствии с ньютоновым законом всемирного тяготения играет роль в движении звездных систем, внутри звездных скоплений и галактик, то есть во всех космических процессах, в которых участвуют и взаимодействуют скопления больших масс вещества. Однако гравитационные поля внутри звездных скоплений и галактик имеют очень сложный характер, движения внутри них изучает звездная астрономия, при этом методы, применяемые ею, отличаются от методов небесной механики. Кроме того, при изучении движений звезд и звездных скоплений кроме сил гравитации следует учитывать силы, возникающие при взаимодействии электрических и магнитных зарядов звезд или их ассоциаций.

Следует заметить, что еще в XVII веке в переписке между Ньютоном и Лейбницем обсуждался вопрос, какой универсальный принцип следует положить в основу расчета характеристик движения небесных тел. Ньютон утверждал, что таким принципом следует считать сохранение момента количества движения в изолированной системе гравитационно взаимодействующих тел. Напротив, Лейбниц полагал, что в качестве такого универсального принципа следует принять закон сохранения энергии в этой системе тел.

Современник Ньютона Э. Галлей (1656-1742 г.г.) открыл первую периодическую комету (1682 г.) и предсказал ее возвращение в 1758 г.; он открыл собственное движение звезд и новые возмущения в движении Луны и планет.

Д’Аламбер Ж. (1717-1783) обосновал теорию возмущений движения планет, а также теорию предварения равноденствий и нутаций.

Д. Клеро (1713-1765 г.г.) разработал новую теорию движения Луны (1751 г.), провел исследования фигуры Земли. На основе изучения движения кометы Галлея в 1759 г. определил момент ее предстоящего прохождения через перигелий.

И. Ламберт (1728-1777 г.г.) ввел понятие двойных звезд, исследовал особенности движения Юпитера и Сатурна. Путем сопоставления яркости звезд пытался оценить их удаленность, исследовал орбиты комет.

Д. Брадлей (1693-1762 г.г.) открыл нутацию земной оси и определил ее период. Наблюдения Брадлея дали материал для определения постоянных прецессии и нутации, а также собственных движений звезд.

Ш. Мессье (1730-1817 г.г.) систематически вел поиск новых комет. В 1781 г. составил каталог туманностей и звездных склонений.

В.Я.Струве (1793-1864 г.г.) принадлежат исследования двойных звезд, оценки параллаксов многих звезд; он обнаружил концентрацию звезд в главной плоскости Млечного пути, составил звездные каталоги.

Лагранж Ж. (1736-1813 г.г) разработал классические методы теории возмущений.

Лаплас П. (1749-1827 г.г.) развил далее методы теории возмущений. Ему удалось доказать, что закон всемирного тяготения полностью объясняет движение планет, если представить их взаимные возмущения в виде рядов. Он доказал также, что эти возмущения имеют периодический характер. В 1780 г. Лаплас предложил новый способ вычисления орбит небесных тел. Лаплас разработал методы исследования устойчивости движения небесных тел. Он пришел к выводу, что кольцо Сатурна не может быть сплошным, так как в этом случае оно было бы неустойчиво, и предсказал открытие сильного сжатия Сатурна у полюсов.

В 1789 г. Лаплас рассмотрел теорию движения спутников Юпитера под действием взаимных возмущений и притяжения Солнца. Он получил полное согласие теории с наблюдениями и установил ряд закономерностей в этих движениях. Лаплас открыл причины ускорения в движении Луны. В 1787 г. он показал, что средняя скорость движения Луны зависит от эксцентриситета земной орбиты, а последний изменяется под действием притяжения планет. Лаплас доказал, что это возмущение долгопериодическое и что впоследствии Луна будет двигаться замедленно. По неравенствам движения Луны Лаплас определил сжатие Земли у полюсов, он разработал также динамическую теорию приливов. Труды Лапласа по небесной механике подытожены в сочинении «Трактат по небесной механике» (т.1-5, 1798-1825 г.г.).

В популярной книге «Изложение системы мира» Лаплас в 1796 г. высказал космогоническую гипотезу об образовании Солнечной системы (Солнца, планет и их спутников) из вращающейся и сжимающейся газовой туманности. Хотя гипотеза Лапласа не смогла объяснить некоторые эффекты движения Солнца и планет (медленное вращение Солнца, прямое вращение планет, обратное движение спутников и движение спутников, период обращения которых меньше периода вращения планеты), она сыграла выдающуюся роль в истории астрономии.

Л.Эйлер (1707-1783 г.г.) в «Теории движения твердого тела» разработал кинематику и динамику твердого тела и дал уравнение его вращения вокруг неподвижной точки, положив начало теории гироскопа. Значительны работы Эйлера по теории движения Луны, движению полюсов Земли.

Астрономические работы К. Гаусса (1777-1855 г.г.) связаны с решением проблемы определения орбит малых планет и исследованием их возмущений. Он разработал метод вычисления орбит планет по трем наблюдениям. Результаты этих исследований Гаусс опубликовал в сочинении «Теория движения небесных тел» (1809 г.). Гаусс разработал метод обработки неравноценных наблюдений (метод наименьших квадратов). Он также обосновал принцип наименьшего принуждения, разработал теорию земного магнетизма, основы теории потенциала.

Бессель Ф. (1784-1846 г.г.) в 1804 г. вычислил орбиту кометы Галлея, в 1838 г. при помощи гелиометра определил параллакс звезды 61 Лебедя, таким образом измерив расстояние до звезд; разработал теорию солнечных затмений, определил массы планет; в 1844 г. обнаружил на основе вычислений наличие спутников у звезд (Сириуса и Проциона), впоследствии увиденных в телескопы.

Теория движения больших планет, разработанная Леверье, до сих пор лежит в основе французского национального астрономического ежегодника.

Дальнейшее развитие теории больших планет получила в работах С. Ньюкомба (1835-1909 г.г.) и Дж. Хилла (1838-1914 г.г.). Ньюкомб впервые обработал ряды наблюдений, охватывающие длительные интервалы времени и на этой основе получил систему астрономических постоянных. Построенная Хиллом теория движения Юпитера и Сатурна используется до настоящего времени при составлении астрономических ежегодников.

В 20-м веке Бюро американских эфемерид (Вашингтонская морская обсерватория) под руководством Д. Брауэра и Дж. Клеменса осуществила работы по переработке планетных теорий. В 1951 г. были опубликованы «Координаты пяти внешних планет». Эта работа была первым успешным применением электронных вычислительных машин к решению задач небесной механики.

В СССР в 1964 г. была разработана аналитическая теория движения Плутона.

Первые теории движения Луны были разработаны А. Клеро, Ж. Д’Алам­бером, Л. Эйлером и П. Лапласом, П. Ганзеном. Ш. Делоне. Современная теория движения Луны основана на работах Дж. Хилла (1886 г.). Построение таблиц Луны на основе метода Хилла было выполнено американским астрономом Э. Брауном. В 1923 г. впервые была дана эфемерида Луны, основанная на таблицах Брауна. С 1970 г. эфемерида Луны в астрономических ежегодниках вычисляется непосредственно по тригонометрическим рядам Брауна без помощи таблиц.

Теория движения четырех галилеевых спутников Юпитера была разработана еще П. Лапласом. В дальнейшем теории движения спутников планет получили развитие. В теории, предложенной В. де Ситтером (1919 г.) и используемой в астрономических ежегодниках, учитывается сжатие Юпитера, возмущения от притяжения спутников Солнцем и взаимные возмущения спутников. Теория движения спутников Сатурна была построена немецким астрономом Г. Струве (1924 г.). Устойчивость спутниковых систем рассмотрена в работах японского астронома Ю. Хагихара (1952 г.).

Источник

НЕБЕСНАЯ МЕХАНИКА

НЕБЕСНАЯ МЕХАНИКА, раздел астрономии, применяющий законы механики для изучения движения небесных тел. Небесная механика занимается предвычислением положения Луны и планет, предсказанием места и времени затмений, в общем, определением реального движения космических тел.

Естественно, что небесная механика в первую очередь изучает поведение тел Солнечной системы – обращение планет вокруг Солнца, спутников вокруг планет, движение комет и других малых набесных тел. Тогда как перемещение далеких звезд удается заметить, в лучшем случае, за десятилетия и века, движение членов Солнечной системы происходит буквально на глазах – за дни, часы и даже минуты. Поэтому его изучение стало началом современной небесной механики, рожденной трудами И.Кеплера (1571–1630) и И.Ньютона (1643–1727). Кеплер впервые установил законы планетного движения, а Ньютон вывел из законов Кеплера закон всемирного тяготения и использовал законы движения и тяготения для решения небесно-механических проблем, не охваченных законами Кеплера. После Ньютона прогресс в небесной механике в основном заключался в развитии математической техники для решения уравнений, выражающих законы Ньютона. Таким образом, принципы небесной механики – это «классика» в том смысле, что и сегодня они такие же, как во времена Ньютона.

Законы движения Ньютона.

Чтобы лучше понять методы и результаты небесной механики, познакомимся с законами Ньютона и проиллюстрируем их простыми примерами.

Закон инерции.

Согласно этому закону, в системе отсчета, движущейся без ускорения, каждое тело сохраняет состояние покоя или прямолинейного и равномерного движения, если на него не действует внешняя сила. Это противоречит положению аристотелевой физики, утверждающему, что для поддержания движения тела требуется сила. Закон Ньютона говорит, что внешняя сила необходима только для приведения тела в движение, для его остановки или для изменения направления и величины его скорости. Темп изменения скорости тела по величине или направлению называется «ускорением» и свидетельствует о том, что на тело действует сила. Для небесных тел обнаруженное из наблюдений ускорение служит единственным указателем действующей на них внешней силы. Понятие о силе и ускорении позволяет с единой позиции объяснить движение всех тел в природе: от теннисного мяча до планет и галактик.

Поскольку объект, движущийся по искривленной траектории, испытывает ускорение, было заключено, что Земля на ее орбите вокруг Солнца постоянно подвергается влиянию силы, которую назвали «гравитацией». Задача небесной механики состоит в том, чтобы определить действующую на небесное тело силу гравитации и выяснить, как она влияет на его движение.

Закон силы.

Если к телу приложена сила, то оно движется ускоренно, причем чем больше сила, тем больше ускорение. Однако одна и та же сила вызывает различное ускорение у разных тел. Характеристикой инертности тела (т.е. сопротивления ускорению) служит его «масса», которую в первом приближении можно определить как «количество вещества»: чем больше масса тела, тем меньше его ускорение под действием заданной силы. Таким образом, второй закон Ньютона утверждает, что ускорение тела пропорционально приложенной к нему силе и обратно пропорционально его массе. Если из наблюдений известны ускорение тела и его масса, то, используя этот закон, можно вычислить действующую на тело силу.

Закон противодействия.

Этот закон утверждает, что взаимодействующие тела прилагают друг к другу равные по величине, но противоположно направленные силы. Поэтому в системе из двух тел, влияющих друг на друга одинаковой по величине силой, каждое испытывает ускорение, обратно пропорциональное его массе. Значит, лежащая на прямой между ними точка, удаленная от каждого обратно пропорционально его массе, будет двигаться без ускорения, несмотря на то, что каждое из тел движется ускоренно. Эту точку называют «центром масс»; вокруг нее обращаются звезды в двойной системе. Если одна из звезд вдвое массивнее другой, то она движется вдвое ближе к центру масс, чем ее соседка.

Законы Кеплера.

Чтобы изучать движение небесных тел, познакомимся с силой гравитации. Лучше всего это сделать на примере взаимного движения двух тел: компонентов двойной звезды или Земли вокруг Солнца (для простоты предполагая, что другие планеты отсутствуют). К таким системам применимы законы Кеплера. В основе их лежит тот факт, что оба взаимодействующих тела движутся в одной плоскости. Это означает, что и сила гравитации всегда лежит в той же плоскости.

Закон эллипсов.

Первый закон Кеплера утверждает, что планеты Солнечной системы движутся по эллипсам, в одном из фокусов которого находится Солнце. Фактически этот закон справедлив только для системы из двух тел, например для двойной звезды. Но и в Солнечной системе он выполняется довольно точно, поскольку на движение каждой планеты в основном влияет массивное Солнце, а все остальные тела влияют несравненно слабее.

Закон площадей.

Если отмечать не только положение планеты, но и время, то можно узнать не только форму орбиты, но и характер движения планеты по ней. Оно подчиняется второму закону Кеплера, утверждающему, что линия, соединяющая Солнце и планету (или компоненты двойной звезды), за равные интервалы времени «заметает» равные площади. Например, эта линия между Солнцем и Землей каждые сутки заметает 2ґ10 14 квадратных километров. Из закона площадей следует, что Солнце притягивает планету строго по прямой, соединяющей их центры. Верно и обратное: для любой центральной силы справедлив второй закон Кеплера.

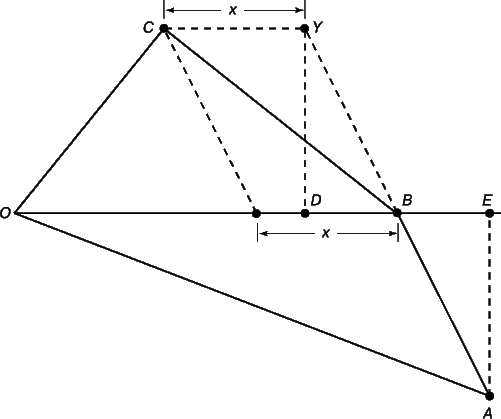
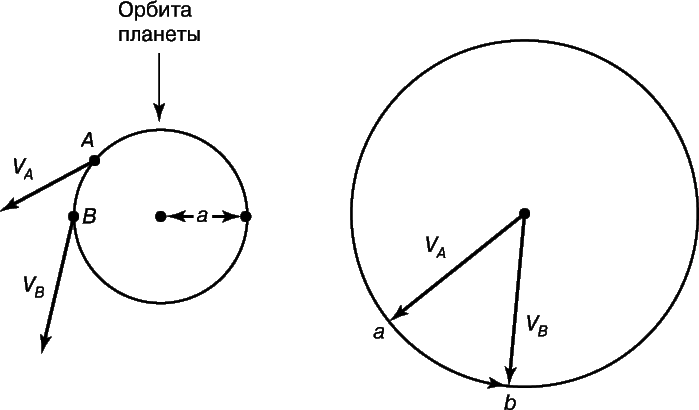
Рассмотрим планету (рис. 1), перемещающуюся из точки A в B за единицу времени. Если бы притяжение к точке O, где расположено Солнце, отсутствовало, то за следующую единицу времени планета переместилась бы в точку Y, такую, что AB = BY. С другой стороны, при наличии притяжения покоящееся в точке B тело переместилось бы за это время на расстояние x. Чтобы найти точку C, в которую действительно переместится планета, проведем прямую CY длиной x параллельно OB. Перпендикуляры, опущенные из точек Y и C на отрезок OB, очевидно, равны между собой. Если отрезок YD есть перпендикуляр из точки Y, а отрезок AE – перпендикуляр из точки A, то и они равны между собой из равенства треугольников YDB и AEB. Следовательно, высоты треугольников OBC и OBA равны, а значит, равны и площади этих треугольников, поскольку OB – их общее основание. Тем самым мы доказали, что за равные времена прямая, соединяющая планету с Солнцем (ее называют «радиусом-вектором» планеты), заметает равные площади. Если бы сила притяжения не была направлена точно к Солнцу, то отрезок CY не был бы параллелен прямой OB, и наше доказательство не было бы справедливым.

Разумеется, приведенное выше доказательство справедливо лишь для бесконечно малых значений углов BOC и BOA. Однако любой отрезок орбиты можно представить как последовательность большого числа таких фигур, поэтому и для него доказательство останется справедливым.

Гармонический закон.

Еще больше можно узнать о силе гравитации из третьего закона Кеплера, связывающего размер планетной орбиты с периодом обращения по ней. Его называют гармоническим законом, поскольку склонный к мистике Кеплер считал эту связь проявлением «небесной гармонии». Закон гласит, что если а – большая полуось эллиптической орбиты планеты, а P – период обращения по ней, то отношение a 3 /P 2 одинаково для всех планет.

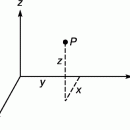
Рассмотрим некоторую планету, обращающуюся вокруг Солнца по круговой орбите радиуса a. Солнце притягивает ее с постоянной по величине силой, сообщая ускорение, необходимое для равномерного изменения направления движения. Найдем это ускорение, вычислив изменение скорости планеты V за единицу времени (рис. 2). За период оборота планеты по орбите, равный 2pa/V, вектор скорости совершает полный поворот. Поэтому изменение скорости за это время равно длине окружности радиуса V. Изменение скорости за единицу времени, т.е. ускорение, составляет

Гармонический закон утверждает, что период обращения планеты зависит только от ее расстояния от Солнца и не зависит от ее массы. Значит, все тела, движущиеся по одной орбите, должны иметь одинаковую скорость.

Закон всемирного тяготения Ньютона.

Анализируя законы Кеплера и наблюдательные данные о движении Луны, Ньютон сформулировал новый закон: каждая частица вещества притягивается к любой другой частице вдоль соединяющей их прямой с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Это всеобщий закон; он не ограничен влиянием Солнца на планеты. Он описывает также взаимодействие двух звезд, планеты и ее спутника, Земли и метеорита, Солнца и кометы. Все вещество во Вселенной подчиняется этому закону, поэтому его называют законом всемирного тяготения. Всеобщность этого закона дополняется его уникальностью: как доказали математики, планетные орбиты имеют вид эллипсов, в фокусе которых находится Солнце, только в том случае, если притяжение меняется обратно пропорционально квадрату расстояния.

Казалось бы, попытка на основе ньютоновых законов движения и гравитации исследовать относительное движение взаимно притягивающихся тел должна привести к выводу знакомых нам законов Кеплера. Но это решительно не так, ибо законы Кеплера справедливы только в том случае, если: 1) взаимодействуют не более двух тел; 2) тела движутся по замкнутым орбитам; 3) масса одного из тел пренебрежимо мала по сравнению с массой другого. Эти условия делают анализ предельно простым, но они совершенно не обязательны для применения законов движения и гравитации. Используя эти общие законы, мы можем пренебречь указанными ограничениями. Сделаем это, отказываясь каждый раз лишь от одного из них.

Во-первых, можно показать, что орбита может быть не только эллипсом (частный случай которого – окружность), но также параболой или гиперболой. Все эти кривые называют «коническими сечениями», поскольку они получаются при пересечении прямого кругового конуса плоскостью. Круг и эллипс – замкнутые кривые; парабола и гипербола – незамкнутые. Спутник, движущийся по замкнутой орбите, совершает одинаковые обороты снова и снова, а спутник, движущийся по незамкнутой кривой, приближается к главному телу с бесконечно далекого расстояния и, пролетев поблизости от него, вновь удаляется на бесконечность.

Во-вторых, можно показать, что «постоянная» величина a 3 /P 2 в гармоническом законе численно равна сумме масс двух взаимодействующих тел, если a выражено в расстояниях Земли от Солнца (в астрономических единицах), P – в периодах обращения Земли (в годах), а масса – в сумме масс Земли и Солнца. Поскольку в Солнечной системе масса любой планеты не превосходит тысячной доли массы Солнца, величины a 3 /P 2 для всех планет различаются не более чем на 0,1%. Будь планеты массивнее, Кеплер не смог бы сформулировать свой гармонический закон. В общем виде этот закон выглядит так:

где M и m – массы компонентов системы, например Земли и Луны или звезд в двойной системе, причем значения масс могут быть любыми. (Все значения величин в этой формуле должны быть выражены в единой системе, например: астрономическая единица, год, масса Солнца.) Этот закон астрономы используют для определения масс различных космических объектов.

Можно также исследовать поведение трех или более взаимно притягивающихся тел. Закон тяготения позволяет вычислить силу, действующую на каждое из тел со стороны остальных, а законы движения – определить, как изменяется от этого его скорость. В случае двух тел их траектории движения могут быть представлены простыми уравнениями Кеплера. Но если тел больше, то это невозможно сделать с помощью конечного числа уравнений.

Этот последний случай наиболее часто встречается в небесной механике Солнечной системы. Важную проблему трех тел представляет система Земля – Луна – Солнце, но и здесь для точного вычисления орбиты Луны приходится учитывать возмущения со стороны других планет (особенно Юпитера и Сатурна), влияние экваториального вздутия Земли и даже влияние приливов, которые Луна вызывает в океанах Земли.

Интерес к классической небесной механике значительно возрос в последние десятилетия в связи с необходимостью расчета орбит искусственных спутников и межпланетных аппаратов. Мощные компьютеры сделали возможным быстрое решение любой небесно-механической задачи с высокой точностью. Впервые для таких расчетов был использован компьютер SSEC фирмы IBM размером с комнату. Для вычисления положений Юпитера, Сатурна, Урана, Нептуна и Плутона с интервалом в 40 сут с 1653 по 2060 ему понадобилось 140 ч; сегодня рядовой компьютер делает это менее чем за 2 с. Теперь с помощью мощнейших компьютеров стало возможным решать такие задачи, которые были совершенно не доступны классической небесной механике: можно проследить на протяжении миллиардов лет эволюцию скопления, состоящего из сотен тысяч звезд; можно детально рассчитать, как исказится форма двух сталкивающихся галактик. Компьютер вдохнул новую жизнь в небесную механику.

Источник