средневзвешенное значение что это

В процессе изучения математики школьники знакомятся с понятием среднего арифметического. В дальнейшем в статистике и некоторых других науках студенты сталкиваются и с вычислением других средних значений. Какими они могут быть и чем отличаются друг от друга?

Средние величины: смысл и различия

Не всегда точные показатели дают понимание ситуации. Для того чтобы оценить ту или иную обстановку, нужно подчас анализировать огромное количество цифр. И тогда на помощь приходят средние значения. Именно они позволяют оценить ситуацию в общем и целом.

Часто в рамках школьного курса изучают и среднее геометрическое. Расчет данного значения базируется на извлечении корня n-ной степени из произведения n-членов. Если брать те же числа: 27, 22, 34 и 37, то результат вычислений будет равен 29,4.

Средневзвешенное значение: особенности

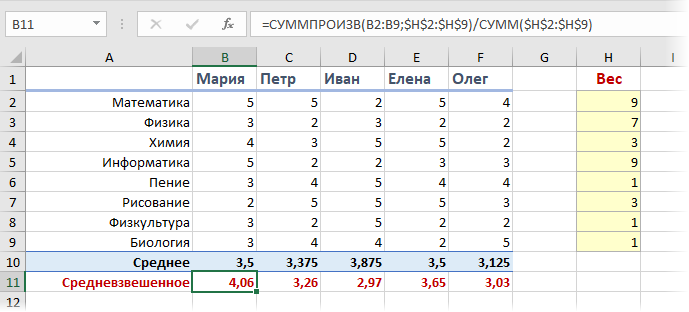
Однако все вышеперечисленные величины могут быть использованы не везде. Например, в статистике при расчете некоторых средних значений важную роль имеет «вес» каждого числа, используемого в вычислениях. Результаты являются более показательными и корректными, поскольку учитывают больше информации. Эта группа величин носит общее название «средневзвешенное значение». Их в школе не проходят, поэтому на них стоит остановиться поподробнее.

В случае средневзвешенных расчетов за «вес» может быть принято количество отгрузок, число работающих в тот или иной день людей, в общем, все что угодно, что может быть измерено и повлиять на конечный результат.

Разновидности

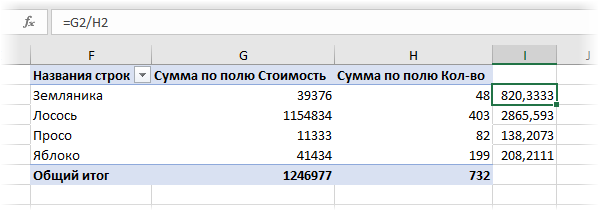
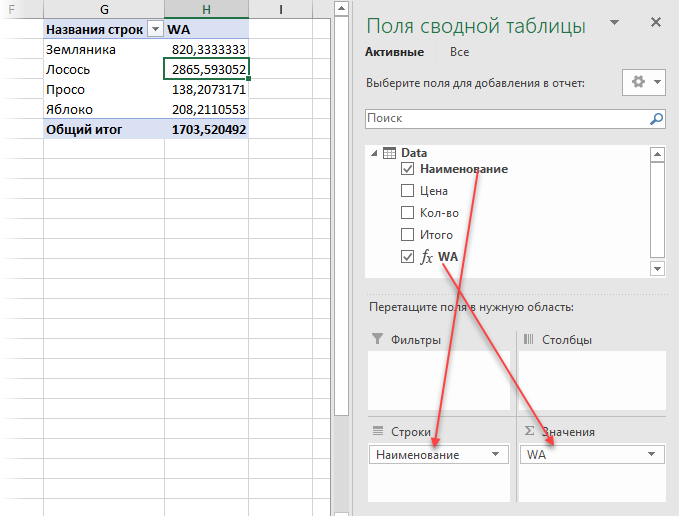
Средневзвешенное значение соотносится со средним арифметическим, рассмотренным в начале статьи. Однако первая величина, как уже было сказано, учитывает также вес каждого числа, использованного в расчетах. Помимо этого существуют также средневзвешенное геометрическое и гармоническое значения.

Имеется еще одна интересная разновидность, используемая в рядах чисел. Речь идет о взвешенном скользящем среднем значении. Именно на его основе рассчитываются тренды. Помимо самих значений и их веса там также используется периодичность. И при вычислении среднего значения в какой-то момент времени также учитываются величины за предыдущие временные отрезки.

Расчет всех этих значений не так уж и сложен, однако на практике обычно используется только обычное средневзвешенное значение.

Способы расчета

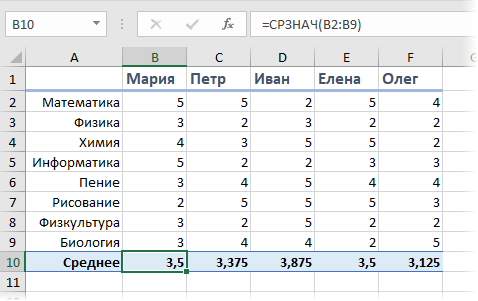
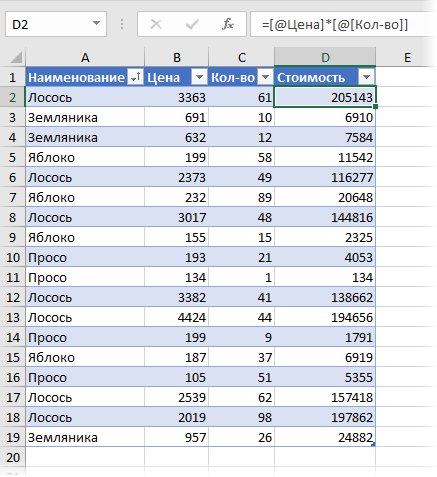
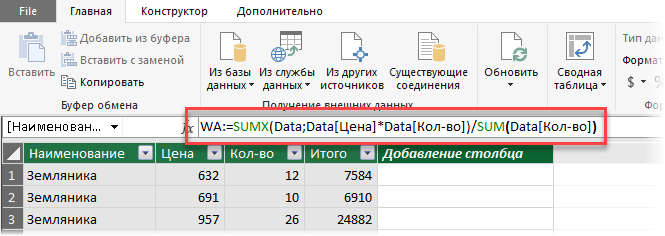
В век повальной компьютеризации нет необходимости вычислять средневзвешенное значение вручную. Однако нелишним будет знать формулу расчета, чтобы можно было проверить и при необходимости откорректировать полученные результаты.

Проще всего будет рассмотреть вычисление на конкретном примере.

Заработная плата (тыс. руб.)	Число рабочих (чел.)
32	20
33	35
34	14
40	6

Необходимо узнать, какая же средняя оплата труда на этом предприятии с учетом количества рабочих, получающих тот или иной заработок.

Итак, расчет средневзвешенного значения производится с помощью такой формулы:

Для примера же вычисление будет таким:

x = (32*20+33*35+3 14+40*6)/(20+35+14+6) = (640+1155+476+240)/75 = 33,48

Источник

СРЕДНЕВЗВЕШЕННОЕ

Смотреть что такое «СРЕДНЕВЗВЕШЕННОЕ» в других словарях:

Средневзвешенное количество циркулирующих обыкновенных акций за период — количество обыкновенных акций, выпущенных и обращающихся на начало периода, скорректированное на количество погашенных, выкупленных эмитентом или выпущенных за период акций, умноженное на временной весовой множитель. По английски: Weighted… … Финансовый словарь

СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ) — (weighted average, weighted mean) Среднее арифметическое значение, в котором учтены веса каждого из чисел, для которых рассчитывается это среднее значение. Например, если какое либо лицо покупает товар тремя партиями, одна из которых – 100 тонн… … Финансовый словарь

СРЕДНЕВЗВЕШЕННОЕ (CРЕДНЯЯ) — (weighted average) Средняя, в которой веса различных членов ряда пропорциональны их значимости. Средняя взвешенная N членов ряда х1, х2. xN находится путем суммирования его членов, умноженных на их веса w1, w2. wN, деленного на сумму… … Экономический словарь

Средневзвешенное количество циркулирующих обыкновенных акций за период — (average share volume) количество обыкновенных акций, выпущенных и обращающихся на начало периода, скорректированное на количество погашенных,выкупленных эмитентом или выпущенных за период акций, умноженное на временной весовой множитель … Экономико-математический словарь

средневзвешенное значение — svertinis aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted average; weighted… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

средневзвешенное значение — svertinis aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted mean vok. Gewichteter arithmetischer Mittelwert, m; gewogener Mittelwert, m; gewogenes Mittelwert, m rus.… … Fizikos terminų žodynas

средневзвешенное значение — svertinis vidurkis statusas T sritis fizika atitikmenys: angl. weighted arithmetic average; weighted average; weighted mean vok. gewogener Mittelwert, m; gewogenes Mittel, n rus. взвешенное среднее, n; средневзвешенное значение, n pranc. moyenne… … Fizikos terminų žodynas

средневзвешенное по времени содержание — 3.2.1 средневзвешенное по времени содержание (time weighted average concentration): Содержание химического соединения в воздухе, усредненное за регламентированный период. Источник … Словарь-справочник терминов нормативно-технической документации

Средневзвешенное количество циркулирующих обыкновенных акций за период — Количество обыкновенных акций, выпущенных и обращающихся на начало периода, скорректированное на количество погашенных, выкупленных эмитентом или выпущенных за период акций, умноженное на временной весовой множитель … Финансы и биржа: словарь терминов

Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора

Источник

Средневзвешенная формула

Формула взвешенного среднего (Содержание)

Средневзвешенная формула

Среднее арифметическое = (X1 + X2 + X3 ………. + Xn) / n

Среднее арифметическое = X1 / n + X2 / n + ………………… + Xn / n

Таким образом, все точки данных имеют одинаковый вес и задаются как 1 / n.

Но допустим, что веса различны и определяются как (w1, w2, w3 …………, wn). Таким образом, формула для средневзвешенного значения определяется как:

Weighted Mean = w1*X1 + w2*X2 + w3*X3……………+ wn*Xn

Примеры формулы взвешенного среднего (с шаблоном Excel)

Давайте рассмотрим пример, чтобы лучше понять формулу взвешенного среднего.

Допустим, у вас есть набор данных с 10 точками данных, и мы хотим рассчитать средневзвешенное значение для этого.

Набор данных: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)

Вес: (20%, 15%, 10%, 10%, 5%, 3%, 2%, 7%, 5%, 13%)

Сначала мы рассчитываем произведение набора данных и весов.

Результат будет таким, как указано ниже.

Точно так же мы рассчитали для всех данных.

Средневзвешенное значение рассчитывается по формуле, приведенной ниже

Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn

Допустим, все веса равны, т.е. 10% для каждого набора данных.

Сначала мы рассчитываем произведение набора данных и весов.

Средневзвешенное значение рассчитывается по формуле, приведенной ниже

Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn

Среднее арифметическое рассчитывается по формуле, приведенной ниже

Среднее арифметическое = (сумма всех точек данных) / количество точек данных

Поэтому, когда все веса равны, среднее арифметическое такое же, как среднее взвешенное

Допустим, у вас есть портфель, в котором у вас есть акции, облигации и товары. Таким образом, в основном у нас есть портфель, в который мы инвестировали в акции, облигации и товары. Ниже приведены веса / пропорции каждого инструмента в вашем портфеле:

Средневзвешенное значение рассчитывается по формуле, приведенной ниже

Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn

Простая средняя доходность портфеля рассчитывается по формуле, приведенной ниже

Простая средняя доходность портфеля = сумма возвратов / количество товаров

объяснение

Актуальность и использование формулы взвешенного среднего

Калькулятор формулы взвешенного среднего

Вы можете использовать следующий калькулятор взвешенного среднего

Рекомендуемые статьи

Источник

Концепция взвешенного среднего или средневзвешенного значения (англ. ‘weighted mean’) неоднократно возникает в портфельном анализе. В среднем арифметическом значении все наблюдения одинаково взвешены с коэффициентом \(1/n\) (или \(1/N\)).

При работе с портфелями ценных бумаг нам нужна более общая концепция взвешенного среднего, позволяющая использовать разные веса для разных наблюдений.

Как рассчитать доходность этого инвестиционного портфеля?

Доходность портфеля явно предполагает усреднение доходов от инвестиций в акции и облигации. Однако значение, которое мы вычисляем, должно отражать тот факт, что акции имеют 70-процентный вес в портфеле, а облигации имеют 30-процентный вес.

Чтобы отразить это взвешивание, нужно умножить доходность инвестиций в акции на 0,70 и доходность инвестиций в облигации на 0,30, а затем суммировать два результата. Эта сумма является примером взвешенного среднего.

Было бы неправильно принимать среднее арифметическое значение доходности инвестиций в акции и облигации, равнозначно взвешивая доходность этих двух классов активов.

Рассмотрим другой портфель, инвестированный в канадские акции и облигации.

Компонент акций портфеля включает в себя канадский индексный Фонд акций RBC, который отслеживает эффективность индекса доходности S&P / TSX.

Облигационный компонент портфеля включает Фонд облигаций RBC, который инвестирует в высококачественные ценные бумаги с фиксированной доходностью, выпущенные правительствами и корпорациями Канады. Менеджер портфеля размещает 60% портфеля в фонд акций и 40% в фонд облигаций.

В Таблице 13 представлена ​​общая доходность этих инвестиций с 2008 по 2012 год.

Таблица 13. Доходность канадских фондов акций и облигаций, 2008-2012 гг.

Формула взвешенного среднего.

Средневзвешенное значение \(\overline X_w\) (читается «X-bar sub-w») для набора наблюдений \( X_1, X_2, \ldots, X_n \) с соответствующими весами \( w_1, w_2, \ldots, w_n \) вычисляется как:

\(\large< \overline_w = \dsum_^w_i X_i> \) (Формула 4)

В контексте инвестиционных портфелей положительный вес представляет актив, удерживаемый в течение длительного времени, и отрицательный вес представляет актив, удерживаемый на короткой позиции.

Формулу взвешенного среднего можно сравнить с формулой для среднего арифметического значения. Если для последовательности наблюдений \( X_1, X_2, \ldots, X_n \) веса \( W_1, W_2, \ldots, W_n \) равны \(1/n\), то формула для взвешенного среднего будет:

Это формула для среднего арифметического. Следовательно, среднее арифметическое является частным случаем взвешенного среднего, в котором все веса равны.

Доходность рассматриваемого портфеля представляет собой средневзвешенную доходность фонда акций и фонда облигаций (вес фонда акций равен 0,60, а вес фонда облигаций: 0,40).

Используя Формулу 4, мы находим, что:

Доходность портфеля за 2008 год =
= W_акцийR_акций + W_{облигаций}R_{облигаций}

Учитывая, что портфельный менеджер инвестировал 60% в акции и 40% в облигации, среднее арифметическое значение обесценило бы инвестиции в акции и переоценило бы вложения в облигации, в результате чего показатель доходности портфеля был бы выше на 3,3 процентных пункта:

Теперь предположим, что портфельный менеджер поддерживает постоянные веса 60% в акциях и 40% в облигациях в течение всех 5-ти лет. Этот метод называется стратегией постоянных пропорций (англ. ‘constant-proportions strategy’).

Предполагая, что портфельный менеджер способен выполнить необходимую перебалансировку, мы можем рассчитать доходность портфеля в 2009, 2010, 2011 и 2012 годах с помощью формулы 4 следующим образом:

Теперь мы можем найти среднее значение для временных рядов доходности за 2008–2012 годы, используя Формулу 3 для среднего арифметического. Средняя доходность инвестиционного портфеля составляет:

Вместо расчета средней доходности по временным рядам годовой доходности, мы можем рассчитать среднюю арифметическую доходность акций и облигаций за 5 лет, а затем применить к этим значениям соответствующие веса: 0,60 и 0,40.

Средняя доходность фонда акций:

Средняя доходность фонда облигаций:

(-0.1 + 11.0 + 6.4 + 8.4 + 3.8)/ 5 = 29.5/5 = 5.9%.

Таким образом, средняя общая доходность портфеля составляет:

что согласуется с нашими предыдущими расчетами.

Пример расчета доходности инвестиционного портфеля как средневзвешенного значения.

В Таблице 14 представлена ​​информация о распределении активов пенсионного плана Канадской вещательной корпорации (CBC) в 2012 году, а также о доходах по этим классам активов в 2012 году.

В Таблице 14 стратегические инвестиции включают в себя инвестиции в недвижимость, частные инвестиции и инвестиции в хедж-фонды. Покрытие облигаций состоит из производных инструментов, используемых для хеджирования процентных ставок и изменений инфляции.

Таблица 14. Распределение активов пенсионного плана CBC в 2012 году.

Распределение активов (вес)

Доходность класса активов (%)

Денежные средства и краткосрочные инвестиции

Облигации с рыночной доходностью

Источник: Canadian Broadcasting Corporation Pension Plan, 2012 Annual Report.

Используя информацию в Таблице 14, рассчитайте средний доход, полученный пенсионным планом в 2012 году.

Решение:

Преобразовав распределение активов в процентах в десятичную форму, мы находим среднюю доходность как средневзвешенную доходность по классам активов.

Средняя доходность портфеля =
= 0.038(1.3%) + 0.337(6.6%) + 0.148(2.9%)
+ 0.104(8.8%) + 0.214(13.3%) + 0.158(9.5%)
+ 0.001(0.8%)
= 0.049% + 2.224% + 0.429% + 0.915% + 2.846%
+ 1.501% + 0.001%
= 8.0%

Рыночные индексы рассчитываются как средневзвешенные значения. Для индексов рыночной капитализации, таких как CAC-40 во Франции или TOPIX в Японии или S&P 500 в США, каждая включенная в индекс акция получает вес, соответствующий ее рыночной стоимости, деленной на общую рыночную стоимость всех акций индекса.

Наши иллюстрации взвешенного среднего значения используют прошлые данные, но они также могут использовать прогнозные данные. Когда мы берем средневзвешенное значение прогнозных данных, называется ожидаемым значением (англ. ‘expected value’).

Предположим, что мы делаем один прогноз для уровня S&P 500 на конец года, предполагая экономический рост, и другой прогноз для уровня S&P 500 на конец года, предполагающий спад экономики.

Если мы умножим первый прогноз на вероятность экономического роста и второй прогноз на вероятность спада, а затем суммируем эти прогнозы, мы рассчитываем ожидаемое значение S&P 500 на конец года.

Если мы используем средневзвешенное значение возможной будущей доходности S&P 500, мы рассчитаем ожидаемую доходность S&P 500. Сумма вероятностей должна быть равна 1, что удовлетворяет условию о весах в уравнении для взвешенного среднего, приведенного в Формуле 4.

Источник

Расчет средневзвешенного значения в Excel

Основная идея

Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:

На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется «Программирование», а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень. Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение.

В бизнесе средневзвешенное часто используется в таких задачах, как:

Расчет средневзвешенного формулами

Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.е. среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:

Так что берем Машу, а Иван пусть поступает в институт физкультуры 😉

Расчет средневзвешенного в сводной таблице

Поднимем ставки и усложним задачу. Допустим, что теперь нам нужно подсчитать средневзвешенное, но не в обычной, а в сводной таблице. Предположим, что у нас есть вот такая таблица с данными по продажам:

Заметьте, что цена на один и тот же товар может различаться. Наша задача: рассчитать средневзвешенные цены для каждого товара. Следуя той же логике, что и в предыдущем пункте, например, для земляники, которая продавалась 3 раза, это должно быть:

=(691*10 + 632*12 + 957*26)/(10+12+26) = 820,33

То есть мы суммируем стоимости всех сделок (цена каждой сделки умножается на количество по сделке) и потом делим получившееся число на общее количество этого товара.

Правда, с реализацией этой нехитрой логики именно в сводной таблице нас ждет небольшой облом. Если вы работали со сводными раньше, то, наверное, помните, что можно легко переключить поле значений сводной в нужную нам функцию, щелкнув по нему правой кнопкой мыши и выбрав команду Итоги по (Summarize Values By) :

В этом списке есть среднее, но нет средневзвешенного 🙁

Можно частично решить проблему, если добавить в исходную таблицу вспомогательный столбец, где будет считаться стоимость каждой сделки:

В общем, как-то все неудобно, трудоемко и нагоняет тоску. Да еще и дополнительный столбец в исходных данных нужно руками делать. Но красивое решение есть.

Расчет средневзвешенного в сводной таблице с помощью Power Pivot и языка DAX

2. Затем щелкните мышью в строку формул и введите туда формулу для расчета средневзвешенного:

Несколько нюансов по формуле:

Источник

• ← сноски постраничные пример что такое
• Не работает пульверизатор на спрее что делать →