сплайн чейн что это

Что такое Supply Chain Management?

В самом начале пути постараюсь дать определение понятию Supply Chain Management и сферам его применения.

Существует несколько вариантов раскрытия данного понятия уважаемыми агентствами, институтами и крупными корпорациями. Объединяя все общепризнанные определения предлагаю следующее:
Supply Chain Management (Управление Цепью Поставок) является интегрированным процессом, приносящим дополнительную ценность клиенту (низкая цена, поставка в срок, качество материалов, сокращение издержек, удовлетворение спроса и т.п.). Ценность обеспечивается координацией и плотным взаимодействием производителя, потребителя, дистрибьютора(провайдера), перевозчика и других участников движения материальных ценностей и услуг от производителя к клиенту. Данный процесс охватывает следующие этапы:
— Планирование (контроль остатков и оборотного капитала)
— Обеспечение качество сырья, материалов, услуг
— Отбор поставщика (подрядчика)
— Организация транспортировки, в т.ч. отбор перевозчиков (жд, авто, фрахт, контейнерные перевозки)
— Складская логистика и внутреннее перемещение на производство
— Оптимизация доставки готовой продукции до потребителя в необходимом количестве
— Решение претензионных обращений
— Реверсивная логистика
При этом, как поставщик так и клиент вовлечены во все процессы, полностью понимая свое место в Supply Chain друг друга.

Т.е. идеальный, наиболее выигрышный для любой компании вариант — когда все эти процессы сконцентрированы в одном структурном подразделении, когда имеется возможность постоянной коммуникации между людьми, руководящими соответствующими службами, чтобы оценить влияние принижаемых решений на судьбу компании в целом, а не на результат отдельных отделов, департаментов, подразделений. Например выполнение KPI отдела закупок (снижение цен), может негативно сказаться на KPI отдела качества, отдела логистики и таких примеров не мало.

Все больше происходит смещение от
— Старой парадигмы, когда в во главу угла компании ставят вертикальную интеграцию, пытаясь все сырье, услуги и компоненты производить самостоятельно, к
— Новой парадигме, когда компании концентрируются на своих основных конкурентных преимуществах/процессах, а по так называемым непрофильным материалам и услугам стараются вступать в долгосрочные отношения, союзы с целью снижения конечной стоимости производимых товаров.В качестве яркого примера можно привести компанию FORD MOTOR COMPANY, которая собиралась поставлять сырье, производить компоненты на своем заводе. Но после ряда не очень успешных экспериментов, было принято решение передать этот процесс ключевым поставщикам, сконцентрироваться только на сборке.

Источник

Supply Chain: Для кого это нужно и что она приносит компании

Предлагаю немного обратиться не к самой Supply Chain, а к ее пользователям. Кто же они, определившие для себя необходимость внедрения Supply Chain в своих организациях?

По статистике в более чем 70% компаний процессы Supply Chain аккумулируют от 70-90% финансовых затрат компании. Т.е. это практически все деньги, которые компания тратит. Оптимизация всего процесса Supply Chain даже на 2% в целом ведет к значительной экономии денег. Самое главное в этом всем смотреть на все процессы, без разделения на транспорт, закупки, склад, сбыт. Увязав все воедино, оценив всю картину, можно принять подчас невидимую на первый взгляд стратегию по закупкам и сбыту.

В 80% крупных компаний Supply Chain включает в себя следующие службы:

Иногда также включают:

При этом вся Supply Chain настроена на потребности конечного клиента. Безусловно, не каждого, а крупных, иначе вариативность Supply Chain была бы значительной и пришлось бы иметь большой штат. Далее, мы дадим комментарии по тому, на каких клиентах более практично ориентироваться для получения максимального эффекта.

Что же принесет внедрение Supply Chain для конкретной компании, если абстрагироваться от всех умных слов и определений в книгах?
Привожу перечень, который выявлен опытным путем.
Мой список следующий:

Конечно, это все детализируется и уточняется. Но, обобщая, думаю, что это полный список. Если есть что добавить, прошу указать это в комментариях!

Помимо этого, стоит отметить, что нельзя, ни в коим случае, думать, что можно создать шаблон, набор ценностей, которые Supply Chain предоставляют, так как все клиенты разные. Соответственно, и ценность Supply Chain каждый раз уникальна.

Источник

Что такое сплайны, для чего они нужны и как с ними работать

Вот основные формы сплайнов, которыми я обычно пользуюсь:

Все сплайны состоят из точек (vertex) и сегментов (segment):

Точки бывают четырех типов:

Чтобы изменить тип точки нужно выделить одну или несколько точек и нажать правую кнопку мыши. В контекстном меню выбрать нужный тип.
В разеделе Modify сплайны имеют несколько вкладок: Rendering, Interpolation, Selection, Soft Selection и Geometry.

Вкладка Rendering:

Вкладка Interpolation:

Вкладка Geometry:

Использование модификатора Shell, на примере создания объемного текста.

Создаем сплайн Text:

В поле Text меняем текст на нужный, изменяем размер (Size). Выбираем и стека модификаторов Shell. Затем задаем нужную степень выдавливания (Inner Amount или Outer Amount)

Модификатор Shell можно применять только к закрытым сплайнам (не имеющим разрывов). Вот пример использование модификатора Shell на сплайны Text, Line, NGon и Star:

Модификатор Sweep.

Сперва создаим любую линию. Я создал Line с прямыми углами (создается с нажатой клавишей Shift)

Далее из списка модификаторов выбираем Sweep и получаем следующий результат:

Модификатор Lathe.

Поздравляю! Вы дошли до самой интересной части урока.
Модификатор Lathe используется для создания объектов имеющих симметрию вращения (это могуть быть кувшины, бокалы, бутылки, колонны, стаканы и много другое).
Все что вам потребуется это нарисовать вертикальную линию в проекции Font и выбирать из списка модификаторов Lathe:

Нам сразу же нужно переместить ось симметрии, для этого нажимаем на плюсик справа от названия модификатора и выбираем Axis. Перемещаем Axis по оси Х :

Теперь проверьте включена ли у вас кнопка Show end result on/off toggle, которая находится под списком модификаторов. Включить её нужно для того, что бы видеть эффект всех модификаторов назначенных объекту:

Далее переходим к редактированию вершин (нажимаем на плюс слева от Line и выбираем Vertex), добиваемся желаемого результата. Можете добавлять\удалять точки, менять их тип и т.д.

Модификатор Lathe имеет несколько параметров, вот основные из них:

На этом третий урок окончен. В этот раз видеоурок состоит из двух частей:

Источник

Теоретические основы сплайн-интерполяции или почему IQ тесты не имеют решения

Доброго времени, Хабр!

Куча времени прошла с того момента, как я написал свою первую статью, и уже почти год с того момента, как пришла в голову идея для второй. В силу многих обстоятельств (в первую очередь – лени и забывчивости), эта идея так и не была реализована ранее, но сейчас я собрался, написал весь этот материал и готов представить его вашему вниманию.

Начну с небольшой вводной. Будучи студентом 4-го, на тот момент, курса бакалавриата, я изучал курс «Компьютерная графика». Много там было разных интересных (и не очень) заданий, но одно прямо особо запало мне в душу: интерполяция кубическими сплайнами с заданными первыми производными на концах интервала. Пользователь должен был задавать значения первых производных, а программа — считать и выводить на экран интерполяционную кривую. Особенность и основная сложность задания заключена в том, что задаются именно первые производные, а не вторые, как в классической постановке сплайн-интерполяции.
Как я ее решал, и к чему оно в итоге пришло, я как раз и изложу в этой статье. И да, если по описанию задачи вы не поняли ни в чем ее смысл, ни в чем сложность, не переживайте, все это я также постараюсь раскрыть. Итак, поехали.

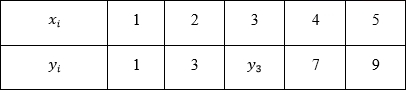
А, нет, погодите один момент. Вот вам два числовых ряда:
a) 2, 4, 6, 8, ?
b) 1, 3, ?, 7, 9

Какие числа должны стоять на месте вопросов и почему? Вы действительно уверены в своем ответе?

Интерполяция

Интерполяция, интерполирование (от лат. inter-polis – «разглаженный, подновлённый, обновлённый; преобразованный») – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. (с) Википедия

Поясню на примерах. Существуют задачи, когда нам требуется узнать, условно, «закон распределения» (взял в кавычки, так как это, вообще говоря, термин из другой области математики) некого параметра по нескольким известным его значениям. Чаще всего речь идет об изменении некого параметра во времени: координаты движущегося тела, температуры объекта, колебания курса валюты, etc. При этом в силу каких-либо обстоятельств у нас не было возможности наблюдать за этим параметром непрерывно, мы могли узнавать его значения лишь в какие-то отдельные моменты времени. Исходными данными в таком случае у нас является множество точек вида value(time), а целью задачи – восстановить кривую, проходящую через эти точки и непрерывно описывающую изменение этого параметра.

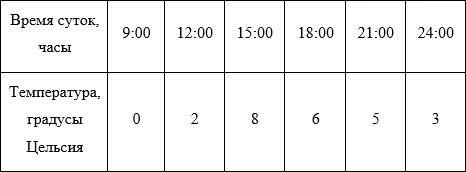
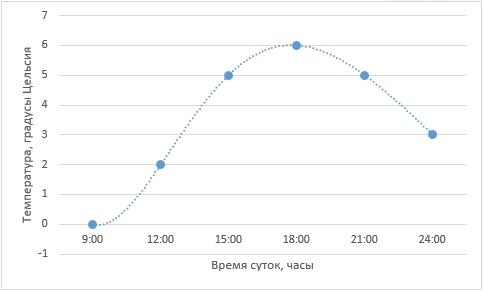
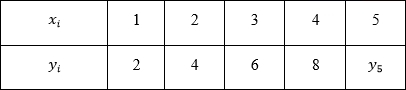
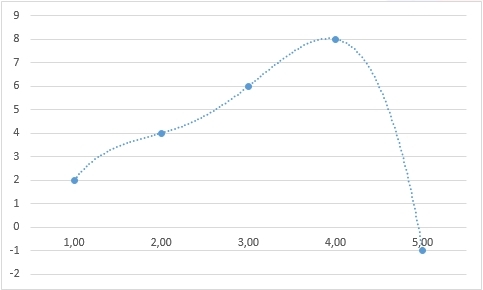
Для дальнейших рассуждений возьмем более простой пример. Представим себе, например, лабораторную работу по географии в каком-нибудь 6-ом классе (кстати, у меня когда-то и правда была такая). Необходимо каждые 3 часа измерять температуру воздуха и записывать данные, а потом сдать учителю график изменения температуры от времени суток. Допустим, по результатам измерений у нас получилась вот такая табличка (данные придуманы случайным образом и никак не претендуют на какую-либо правдоподобность):

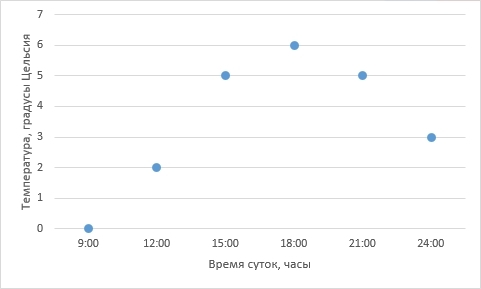
Отобразим полученные данные на графике:

Собственно, данные записаны и отражены на графике. Мы вплотную подошли к задаче интерполяции – как по имеющимся точкам восстановить плавную кривую?

Количество условий и степень интерполирующего полинома

Можем ли мы вообще гарантировать, что такая функция, которая соединяет все заданные точки, вообще существует?

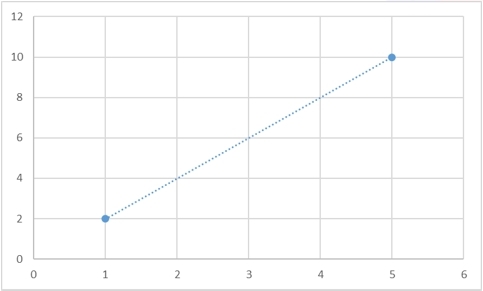
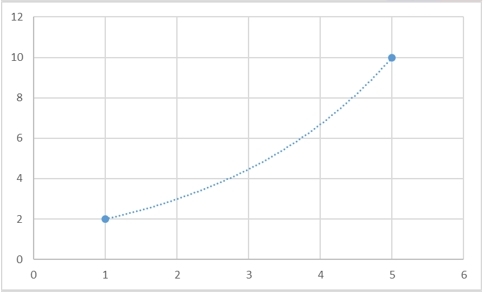
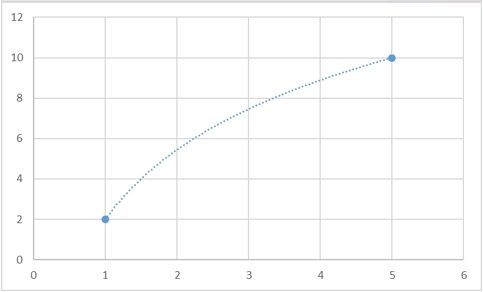
Да, такая функция гарантированно существует, и более того, таких функций будет бесконечно много. Для любого набора точек можно будет придумать сколько угодно много функций, которые через них будут проходить. И вот несколько примеров того, как две точки можно соединить разными способами:

Однако есть и способ задать интерполяционную кривую однозначно. В самом классическом случае, в качестве интерполяционной кривой берут полином:

Для того, чтобы провести через имеющиеся точки такой полином единственным образом, необходимо и достаточно, чтобы степень полинома была на 1 меньше, чем количество условий (я специально выделил это слово, потому что в конце этого раздела я вернусь к этой формулировке). Пока что, простоты ради, условием будут являться координаты точки. Говоря человеческим языком, через 2 точки однозначным образом можно провести прямую (полином 1-ой степени), через 3 точки – параболу (полином 2-ой степени) и т.д.

Возвращаясь к нашей задаче с температурой – в ней мы определили 6 точек, значит, для того, чтобы провести полином единственным образом, он должен быть 5-ой степени

Интерполирующий полином тогда будет выглядеть так:

А сейчас следует сделать важное замечание и пояснить, что я имел ввиду под «условием». Полином можно задать не только координатами точек, через которые он проходит, условиями могут быть любые параметры этого полинома. В простейшем случае это действительно координаты точек. Но в качестве условия можно взять, например, первую производную этого полинома в какой-либо из точек. Вторую производную. Третью производную. В общем, любую возможную производную в любой из точек, в которой этот полином существует. Поясню на примере:
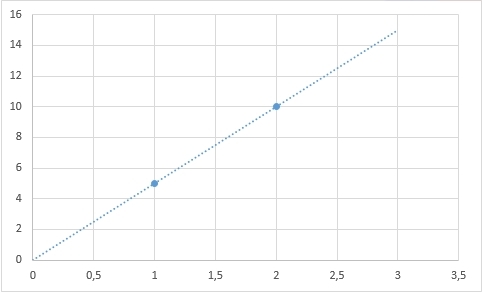
Прямую можно задать однозначно, как я уже говорил, двумя точками:

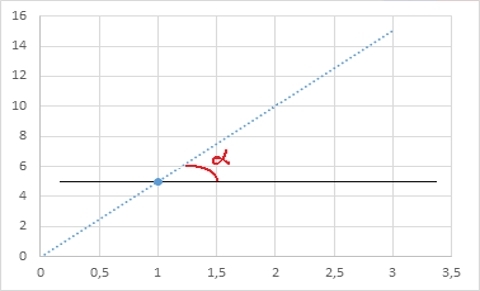
Ту же прямую, с другой стороны, можно определить координатой одной точки и углом наклона альфа к горизонтали:

С полиномами более высоких степеней можно использовать и более сложные условия (вторая производная, третья производная, etc.), и каждый такой параметр будет идти в общий счет количества условий, которые однозначным образом определят этот полином. Чтобы не быть голословным, вот еще пример:

Пусть нам заданы такие три условия:

Условий три, значит, мы хотим получить полином второй степени:

Подставляем

Считаем первую производную и считаем

Считаем вторую производную и считаем

Отсюда получаем, что наш полином выглядит так:

Интерполяция кубическими сплайнами

Вот, по тиху, мы и подбираемся к моей задаче. Полиномиальная интерполяция – не единственно возможный способ интерполяции. Среди всех прочих методов существует метод интерполяции кубическими сплайнами.

Принципиальное отличие идеи сплайн-интерполяции от интерполяции полиномом состоит в том, что полином один, а сплайн состоит из нескольких полиномов, а именно их количество равно количеству инервалов, внутри которых мы производим интерполяцию. В примере с нашей температурой воздуха, в которой у нас определено 6 точек, у нас будет 5 интервалов – соответственно, у нас будут 5 полиномов, каждый на своем интервале.

Каждый из этих полиномов – это полином третьей степени (строго говоря, степени не выше третьей, так как на каком-то из интервалов интерполирующая кривая может становиться квадратичной параболой или даже линейной функцией, но в общем случае это все-таки полином именно третьей степени). Записывая вышесказанное формульно, получим что все наши точки будут соединены некоей кривой , где каждый – это полином третьей степени, а именно:

Возвращаясь к рассказанному в предыдущем пункте, для того, чтобы однозначно задать один полином 3-ей степени, необходимо 4 условия. В этой задаче у нас 5 полиномов, то есть, чтобы задать их все, нам нужно суммарно 5∙4=20 условий. И вот как они получаются:

1) Первый полином определен на первой и второй точках – это два условия. Второй полином определен на второй и третьей точках – еще два условия. Третий полином, четвертый, пятый – каждый из них определен на 2-х точках – суммарно это дает 10 условий.

2) Для каждой промежуточной точки из множества (а это 4 точки с временами 12:00, 15:00, 18:00, 21:00) должно выполняться условие, что первые и вторые производные для левого и правого полиномов должны совпадать. Формульно:

По два таких условия на каждую из промежуточных точек дает еще 8 условий. Следует добавить, что мы задаем только сам факт равенства, а какое конкретно значение они при этом принимают – это совершенно иная задача и считается она довольно сложно.

3) Остаются два условия, которые пока еще не определены. Это так называемые «граничные условия», от задания которых и зависит, какой именно сплайн получится. Обычно задают вторые производные на концах интервала равными 0:

Если сделать так, то мы получим так называемый «естественный сплайн». Для вычисления таких сплайнов написано уже огромное количество библиотек, бери и используй любую.

Отличие моего задания от классической постановки задачи, мои размышления над заданием и само решение

И вот мы подошли к условию моей задачи. Преподаватель придумал такое задание, что задаваться должны первые производные и на левом и правом концах интервала, а программа должна считать интерполирующую кривую. А для такого требования готовых алгоритмов я не нашел…
Я, разумеется, не стану описывать весь твой «творческий» путь от момента, когда я услышал задание, до того, как я его сдал. Расскажу лишь саму идею и покажу ее реализацию.

Сложность задания состоит в том, что, задавая первые производные на концах интервала, да, мы задаем этот сплайн. Теоретически. А вот посчитать его на практике – задача довольно сложная и совершенно неочевидная (желающие могут посмотреть код нахождения естественного сплайна на Вики – ru.wikipedia.org/wiki/Кубический_сплайн – и попробовать его понять хотя бы). Разумеется, я совершенно не хотел провести кучу времени, закопавшись в матан и пытаясь вывести нужные мне формулы. Я хотел более простое и элегантное решение. И я его нашел.
Рассмотрим наш сплайн и возьмем первый из его интервалов. На этом интервале уже заданы 3 условия:

— задается пользователем

Для того, чтобы однозначно задать кубический полином на этом интервале, нам не хватает еще лишь одного условия. Но мы можем его просто придумать! Возьмем вторую производную и положим ее равной, например, 0:

— ничем не обоснованное предположение

Таким образом, зная эти 4 условия, мы полностью определяем этот полином. Зная все параметры этого полинома, мы можем вычислить значения первой и второй производных на второй точке, и поскольку они совпадают со значениями первой и второй производной для полинома на втором интервале, это приводит к тому, что мы также определяем и второй полином:

— вычисляется из

— вычисляется из

Аналогично мы считаем третий полином, четвертый, пятый и так далее, сколько бы их ни было. То есть, по факту, воссоздаем весь сплайн. Но поскольку мы взяли совершенно случайным образом, это приведет к тому, что производная , заданная пользователем на правом конце сплайна, не будет совпадать с производной , которая получилась у нас в ходе таких вычислений. Но получается, что значение производной на правом конце сплайна – это функция, зависящая от значения второй производной на левом конце:

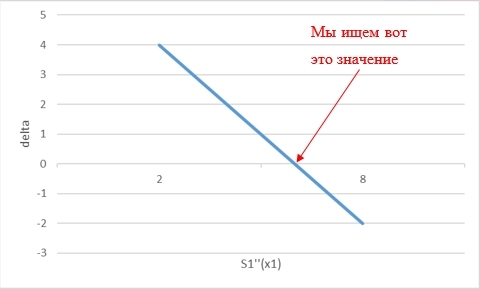
А поскольку такой сплайн, который бы удовлетворял заданным условиям, гарантированно существует, и существует в единственном экземпляре, это значит, что мы можем рассмотреть разность:

и попытаться найти такое значение , при котором обращалась бы в 0 – и это будет тем самым правильным значением , которое строит искомый пользователем сплайн:

Самое замечательное в моей идее то, что эта зависимость оказалась линейной (вне зависимости от количества точек, через которые мы проводим сплайн. Этот факт доказан теоретическими подсчетами), а значит можно случайным образом взять любые два начальные значения и , посчитать и , и сразу же посчитать то самое верное значение, которое построит нам искомый сплайн:

Итого, мы гарантированно находим искомый сплайн за 3 прогонки таких вычислений.

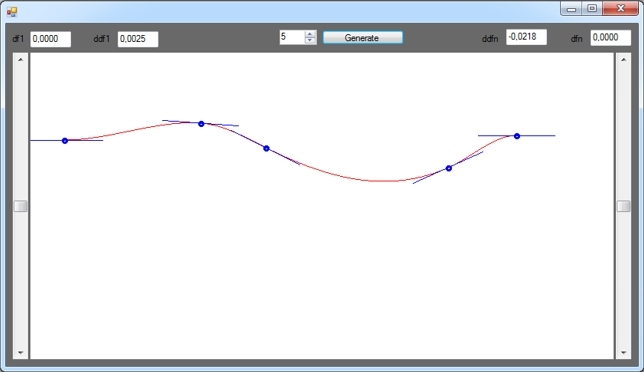
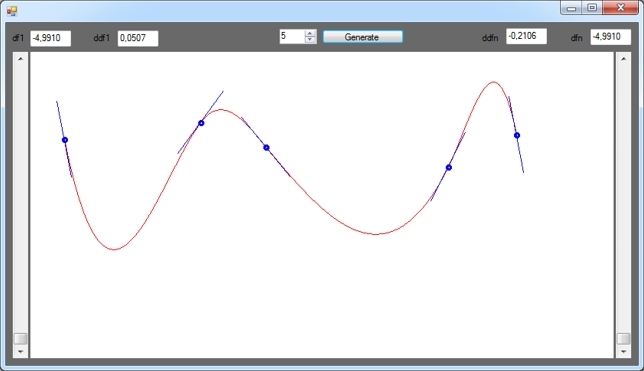
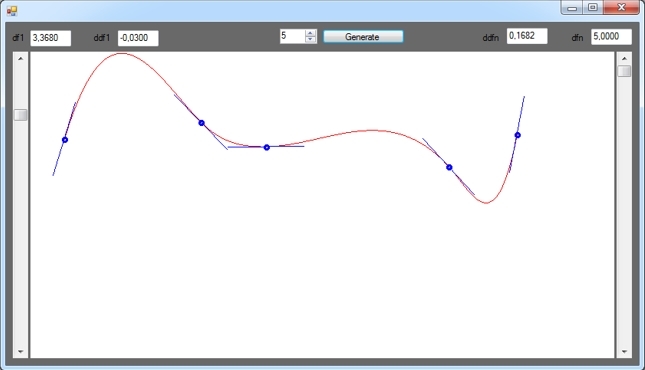
Немного кода и скриншотов программы

Синие отрезки — это первые производные сплайна в соответствующих его точках. Добавил такой вот графический элемент для большей наглядности.

Достоинства и недостатки алгоритма

Признаюсь честно, я не проводил сколь-либо серьезного анализа. По-хорошему стоило бы написать тесты, проверить, как оно работает в разных условиях (мало/много точек интерполяции, равное/произвольное между точками, линейные/квадратные/кубические/тригонометрические/etc. функции и так далее), но я этого не сделал, простите 🙂

Навскидку можно сказать, что сложность алгоритма — O(N), так как, как я уже говорил, вне зависимости от количества точек, достаточно двух прогонов вычислений, чтобы получить правильное значение второй производной на левом конце интервала, и еще одного, чтобы построить сплайн.

Впрочем, если кому-то захочется покопаться в коде и провести какой-нибудь более подробный анализ этого алгоритма, я буду только рад. Напишите мне разве что о результатах, мне было бы интересно.

Так а в чем провинились тесты IQ?

В самом начале статьи я написал два числовых ряда и попросил их продолжить. Это довольно частый вопрос во всяких IQ тестах. В принципе, вопрос как вопрос, но если копнуть чуть глубже, окажется, что он довольно бредовый, потому что при некотором желании можно доказать, что «правильного» ответа на него не имеется.

, где в качестве мы берем само число, а в качестве – порядковый номер этого числа. Какое значение должно быть на месте ?

Мысль, к которой я стараюсь плавно подвести – это то, что мы можем подставить абсолютно любое значение. Ведь что по факту проверяют такие задачи? Способность человека найти некое правило, которое связывает все имеющиеся числа, и по этому правилу вывести следующее число в последовательности. Говоря научным языком, здесь стоит задача экстраполяции (задача интерполяции состоит в том, чтобы найти кривую, проходящую через все точки внутри некоторого интервала, а задача экстраполяции – продолжить эту кривую за пределы интервала, «предсказав» таким образом поведение кривой в дальнейшем). Так вот, экстраполяция не имеет однозначного решения. Вообще. Никогда. Если бы было иначе, люди давным-давно бы предсказали прогноз погоды на всю историю человечества вперед, а скачки курса рубля никогда не были бы неожиданностью.

Разумеется, предполагается, что верный ответ в этой задаче все-таки есть и он равен 10, и тогда «закон», связывающий все эти числа, – это

Однако возьмем любое другое значение – и мы также сможем найти закон, который бы обосновывал именно его:

Хорошо, с экстраполяцией разобрались, она не имеет однозначного решения даже теоретически. Но, быть может, мы сможем найти пропущенное число во втором ряду?

Я считаю, верный ответ . Кто сможет оспорить? 🙂

Источник