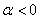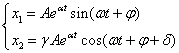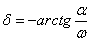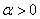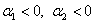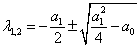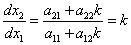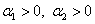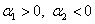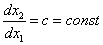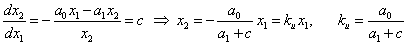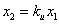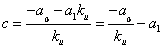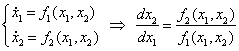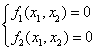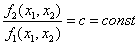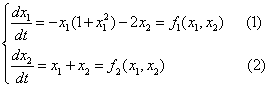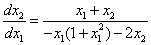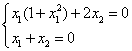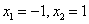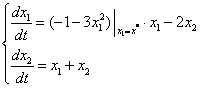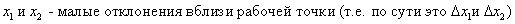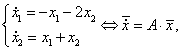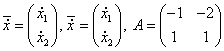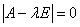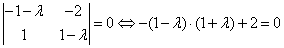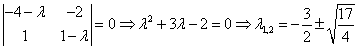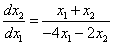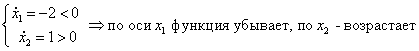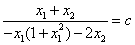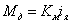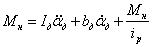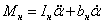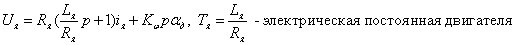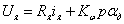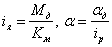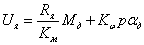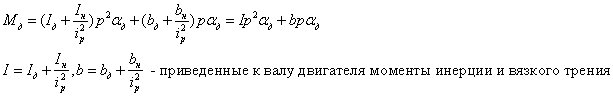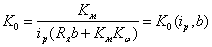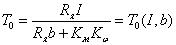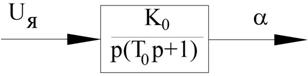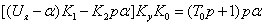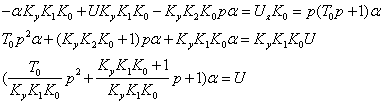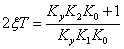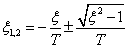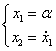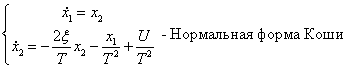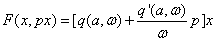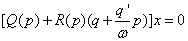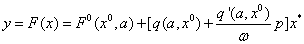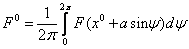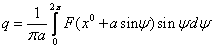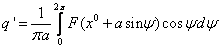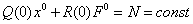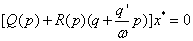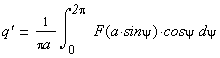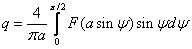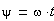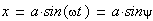полу устойчивый предельный цикл

Большая Энциклопедия Нефти и Газа

Полуустойчивый предельный цикл

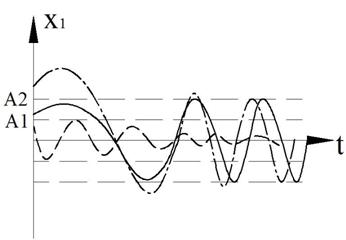
При полуустойчивом предельном цикле в зависимости от его вида и начальных условий фазовая траектория уходит к состоянию покоя или неограниченно удаляется, проходя через предельный цикл либо минуя его. [2]

При совпадении отрезков K N и KN появляется полуустойчивый предельный цикл O2KNOZMPO2 ( рис. 34 6), в связи с чем система регулирования становится неустойчивой: во-первых, при малейших случайных флуктуациях изображающая точка сходит с полуустойчивого предельного цикла во внешнюю область и удаляется бесконечно далеко от положения равновесия; во-вторых, чтобы изображающая точка периодически двигалась по этому циклу, она должна не только попадать в особую точку О %, но и затем выводится флуктуациями на фазовую траекторию О2К, что мало вероятно. [8]

При известном виде области притяжения положения равновесия строят вырожденные полуустойчивые предельные циклы ; для этого прежде всего решается вопрос о числе предельных циклов. [9]

При совпадении отрезков K N и KN появляется полуустойчивый предельный цикл O2KNOZMPO2 ( рис. 34 6), в связи с чем система регулирования становится неустойчивой: во-первых, при малейших случайных флуктуациях изображающая точка сходит с полуустойчивого предельного цикла во внешнюю область и удаляется бесконечно далеко от положения равновесия; во-вторых, чтобы изображающая точка периодически двигалась по этому циклу, она должна не только попадать в особую точку О %, но и затем выводится флуктуациями на фазовую траекторию О2К, что мало вероятно. [14]

Источник

Полу устойчивый предельный цикл

Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.

Рассмотрим автономные системы второго порядка:

Будем полагать, что правые части системы f₁(x₁, x₂), f₂(x₁, x₂) непрерывно дифференцируемы в области определения, т.е. справедлива теорема существования и единственности.
Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx₁/dt и dx₂/dt зависят только от x₁ и x₂. Автономные системы называют также динамическими системами.

Пусть x₁= j ₁(t), x₂= j ₂(t) — решение автономной системы второго порядка. Тогда уравнения

задают в параметрической форме кривую на плоскости (x₁, x₂). Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Именно поэтому автономные системы второго порядка принято называть автономными системами на плоскости.

ПРИМЕР 1. Виды фазовых кривых.

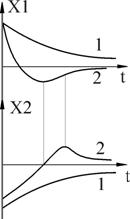
ПРИМЕР 2. Устойчивый предельный цикл.

ПРИМЕР 3. Неустойчивый предельный цикл.

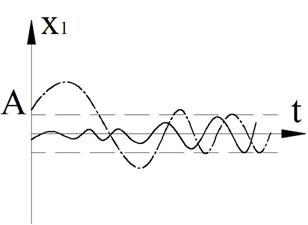
ПРИМЕР 4. Полуустойчивый предельный цикл.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

2. ,

, , ,

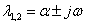
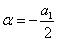
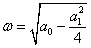
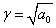
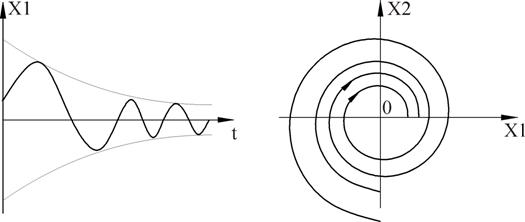
Рисунок 19 – Фазовый портрет и переходный процесс

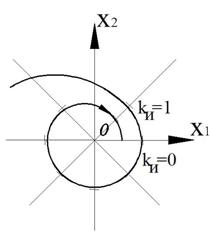
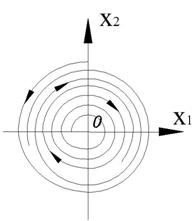
Фазовый портрет представляет собой логарифмическую спираль, сходящуюся к нулю.

Точка (0,0) – особая точка типа «устойчивый фокус».

3. ,

, , ,

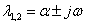
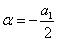
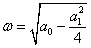
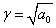
Фазовый портрет представляет собой логарифмическую спираль, рассходящуюся от нулю.

Точка (0,0) – особая точка типа «неустойчивый фокус».

4. ,

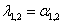
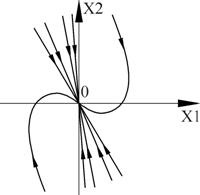
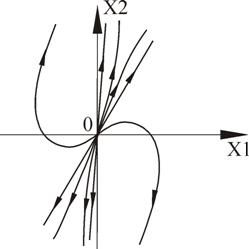
Рисунок 21 – Фазовый портрет

Рисунок 22 – Переходные процессы

Асимптоты: ,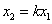

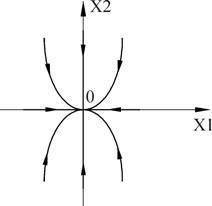
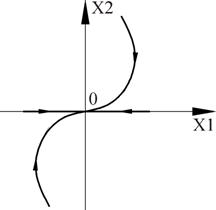
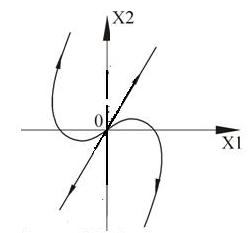
Точка (0,0) – особая точка типа «устойчивый узел».

Вырожденный случай получаем, когда корни одинаковы.

Если матрица в уравнении Коши имеет диагональный вид, то фазовый портрет имеет вид

Рисунок 24 – Частный случай фазового портрета системы

Если матрица имеет диагональный вид и корни равны, то имеем случай

5. ,

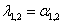
Рисунок 26 – Фазовый портрет

Рисунок 27 – Переходный процесс

Вырожденный случай получаем, когда корни одинаковы.

Рисунок 28 – Вырожденный неустойчивый узел

Если матрица в уравнении Коши имеет диагональный вид, то фазовый портрет имеет следующий вид

Если матрица имеет диагональный вид и корни равны, то имеем случай на рис. 35

6. ,

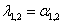
Рисунок 31 – Фазовый портрет

Рисунок 32 – Переходный процесс

Если матрица А имеет диагональный вид, то фазовый портрет изменится следующим образом.

Для уточнения фазовых траекторий используется метод изоклин.

Изоклина – это линия, соединяющая точки фазовых траекторий с одинаковым наклоном касательных. Для линейных систем изоклины представляют собой прямые и проходят через точку (0;0).

Изоклина определяется следующим образом:

Рисунок 34 – Уточнение фазового портрета методом изоклин

Фазовые портреты нелинейных систем.

Неопределенность:

В отличие от линейных систем, в нелинейных системах могут быть и особые линии.

Особые точки те же: центр, узел, фокус, седло и т.д.

Особые линии: устойчивый предельный цикл (фазовая траектория замкнута), неустойчивый предельный цикл, линия устойчивого положения, сепаратрисса (линия, разделяющая области с разным видом фазовых траекторий) и т.д.

Для выявления вида особых точек уравнение системы линеаризуется в их окрестности, определяются корни характеристического уравнения линеаризованной системы.

Уравнение изоклин:

Типовые случаи фазовых портретов нелинейных систем.

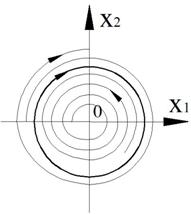
1. Устойчивый предельный цикл (автоколебания).

Фазовая траектория стремится к предельному циклу, следовательно, цикл устойчив.

Рисунок 35 – Фазовый портрет

Рисунок 36 – Переходный процесс

В данном случае система неустойчива в малом (точка (0;0) – неустойчивый фокус), но устойчива – в большом. Т.е. в малых значениях она будет расходиться, а при больших начальных условиях

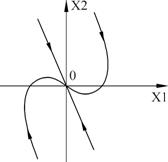
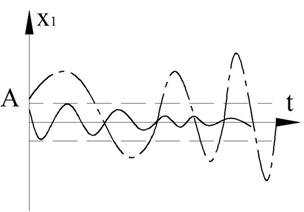
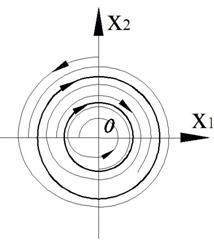
2. Неустойчивый предельный цикл.

Рисунок 37 – Фазовый портрет

Рисунок 38 – Переходный процесс

Система в малом становится устойчивой (точка (0;0) – неустойчивый фокус), а в большом – неустойчивой.

Практически, неустойчивый предельный цикл ограничивает область начальных условий, в пределах которой система устойчива.

3. Несколько предельных циклов.

Рисунок 39 – Фазовый портрет

Рисунок 40 – Переходный процесс

Внешний предельный цикл устойчив, внутренний – неустойчив.

Рисунок 41 – Особая линия типа «сепаратриса»

Сепаратрисcа – особая линия, разделяющая области с различным видом фазовых траекторий.

Три особых точки: «центр» и две типа «седло». Всего на фазовой плоскости образовано 5 областей.

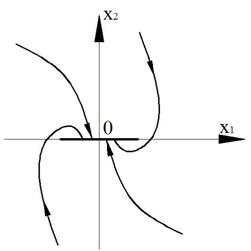
5. Отрезок установившихся состояний (отрезок покоя).

Фазовая траектория только входит в отрезок покоя. На отрезке скорость равна нулю (покой).

Рисунок 42 – Особая линия типа «отрезок покоя»

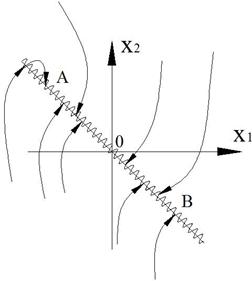
6. Скользящий процесс.

Рисунок 43 – Скользящий процесс

Если траектория приходит не на отрезок AB, то она преломляется на линии скользящего процесса и затем возвращается на отрезок.

При попадании на отрезок скользящего процесса, система начинает двигаться по линии скользящего процесса в направлении точки (0,0)

Практическое значение: в данном случае мы получаем желаемый переходный процесс с заданным законом движения. Это достижимо, если организовать соответствующее управление (нелинейный закон управления), что возможно далеко не всегда.

Рисунок 44 – Движение по линии скользящего процесса

В результате получаем процесс движения по отрезку скользящего процесса в виде колебаний относительно отрезка с амплитудой, стремящейся к нулю, и частотой, стремящейся к бесконечности.

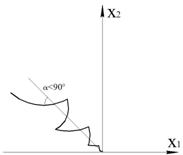
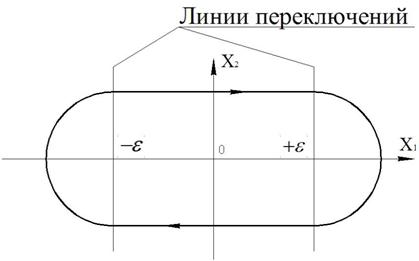
7. Линия переключений (нелинейный закон управления).

Рисунок 45 – Фазовый портрет системы

Пример. Построить фазовый портрет для системы, описываемой следующими уравнениями:

Условие 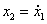не выполняется, следовательно направление фазовых траекторий может быть произвольным.

Разделим уравнение (2) на уравнение (1), получим дифференциальное уравнение фазовой траектории:

Особые точки и линии:

Решение дает 3 особые точки:

1) 2) 3)

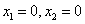
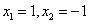
Для определения типа особых точек необходимо линеаризовать уравнение нелинейной системы в окрестности этих особых точек:

Далее символподразумевается, но не пишется.

1)

Для определения типа особой точки решаем характеристическое уравнение:

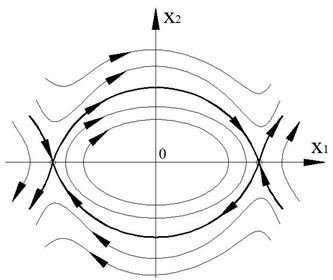
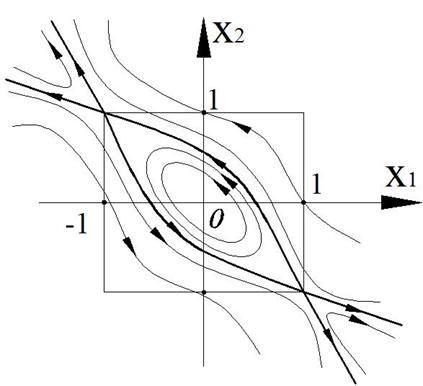
В итоге получаем чисто мнимые корни. Особая точка типа «центр» (фазовая траектория – эллипсы).

2)

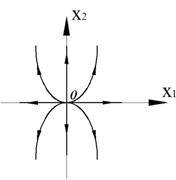
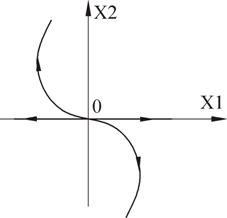
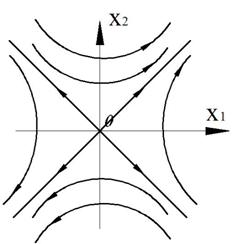
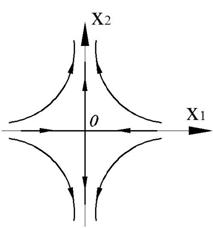
Корни вещественные, разного знака. Особая точка типа «седло».

, k – коэффициент наклона асимптоты

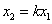
Асимптоты действительны только в малой окрестности точки (1;-1)

3)

Далее аналогично пункту 2)

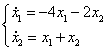
Определим направление фазовых траекторий: возьмем точку 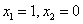и подставим в исходное нелинейное уравнение системы:

при с =1 (наклон касательной 45 о ): 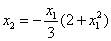, изоклина пройдет через все особые точки.

Таким образом, получаем фазовый портрет

Рисунок 46 – Фазовый портрет

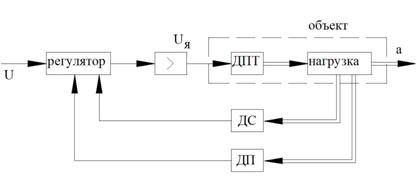
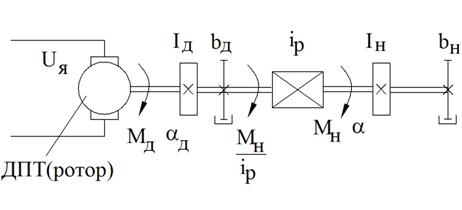
Изображение переходных процессов на фазовой плоскости на примере электромеханического следящего привода.

ДПТ – двигатель постоянного тока

ДС – датчик скорости

— механическая связь

— электрическая связь

— угол поворота выходного вала редуктора

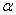
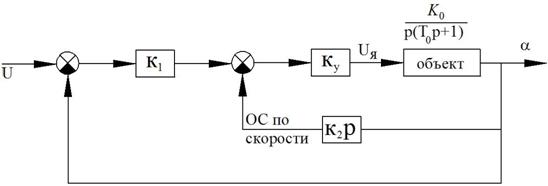
Рисунок 47 – Структурная схема электромеханического следящего привода

Будем считать, что характеристики ДС и ДП линейные.

Пример 1. Следящий привод. Нагрузка: инерционная и вязкое трение.

Рисунок 48 – Структурная схема механической части объекта

— момент инерции двигателя

— момент инерции нагрузки

— передаточное отношение редуктора

— вязкое трение нагрузки

— коэффициент противоЭДС

— коэффициент усиления по моменту

— уравнение ДПТ

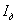
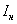
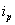
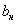
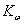
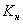
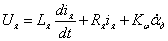
Введем допущение: в рабочем режиме ДПТ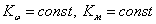(в реальной жизни – гистерезис)

Введем допущение: пренебрегаем электрической постоянной двигателя (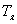на два порядка меньше, чем электромеханическая постоянная).

Уравнение моментов, приведенных к валу двигателя:

, где

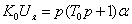
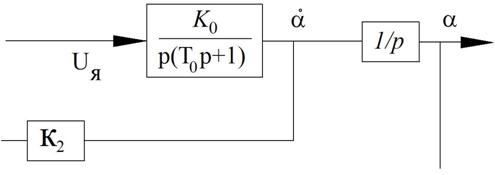
Рисунок 49 – Объект управления

— описание объекта управления (интегрирующее звено с запаздыванием)

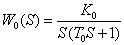
Необходимо найти уравнение регулятора:

Рисунок 50 – Пропорциональный интегральный регулятор

Обратная связь по скорости математически представлена верно, но на практике так делать нельзя из-за шумов (при дифференцировании не будет асимптоты).

При моделировании для исключения шумов необходимо изменить схему следующим образом:

Рисунок 51 – Изменения в схеме для моделирования

Уравнение регулятора с усилителем:

,

— колебательное звено.

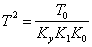
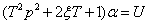
Обозначим:

Фазовые портреты при U=0

В соответствии уравнение линеаризованной системы принимает следующий вид:

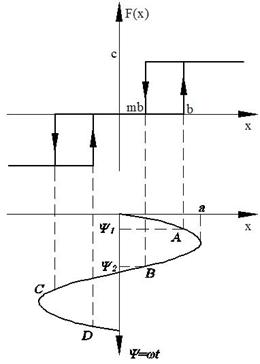
2) Вычисления коэффициентов гармонической линеаризации для несимметричных колебаний

Причины несимметричных колебаний:

1) Несимметричные входные колебания;

Решения будем искать в виде: x = x 0 + asin(ωt) = x 0 +x*, где x*= asin(ωt)

Уравнение системы можно разбить на 2 уравнения: для постоянной составляющей и для гармонического сигнала

3) Вычисление коэффициентов гармонической линеризации для симметричных колебаний

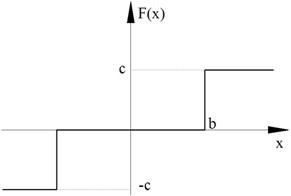
Упрощения: для однозначной нечётной симметричной функции F(x) коэффициент q`=0

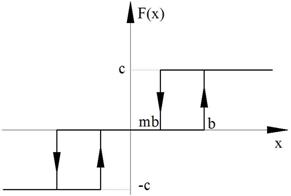
Рисунок 96. Случай а)

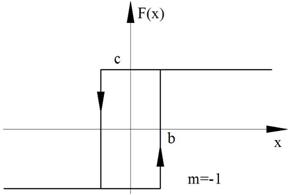
Рисунок 97. Случай б)

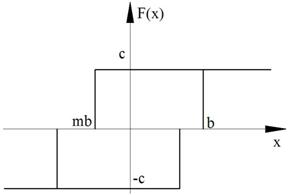
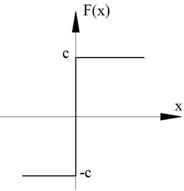
Рисунок 98. Случай в)

Рисунок 99. Случай г)

Рисунок 100. Случай д)

Чтобы распечатать файл, скачайте его (в формате Word).

Источник