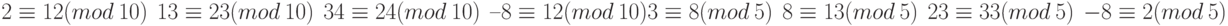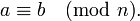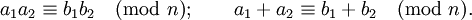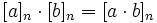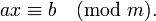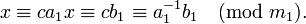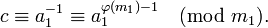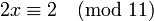поле вычетов по модулю

Модульная арифметика

2.2. Модульная арифметика

Операции по модулю

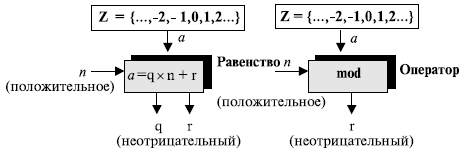
Как показано на рис. 2.9, оператор по модулю ( mod ) выбирает целое число ( a ) из множества Z и положительный модуль ( n ). Оператор определяет неотрицательный остаток ( r ).

Мы можем сказать, что

Найти результат следующих операций:

Система вычетов: Zn

Сравнения

Рисунок 2.11 показывает принцип сравнения. Мы должны объяснить несколько положений.

Система вычетов

Круговая система обозначений

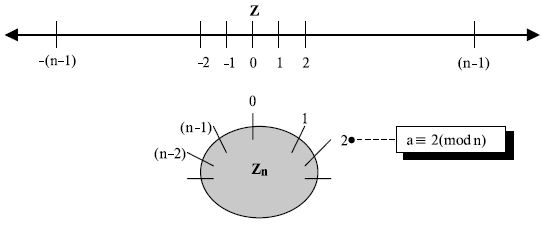
Операции в Zn

Выполните следующие операторы (поступающие от Z_n ):

а. Сложение 7 и 14 в Z₁₅

б. Вычитание 11 из 7 в Z₁₃

в. Умножение 11 на 7 в Z₂₀

Ниже показаны два шага для каждой операции:

Выполните следующие операции (поступающие от Z_n ):

a. Сложение 17 и 27 в Z₁₄

b. Вычитание 43 из 12 в Z₁₃

Ниже показаны два шага для каждой операции:

Свойства

Первое свойство: (a + b) mod n = [(a mod n) + (b mod n)] mod n

Третье свойство: (a x b) mod n = [(a mod n) x (b mod n)] mod n

Рисунок 2.14 показывает процесс до и после применения указанных выше свойств. Хотя по рисунку видно, что процесс с применением этих свойств более длинен, мы должны помнить, что в криптографии мы имеем дело с очень большими целыми числами. Например, если мы умножаем очень большое целое число на другое очень большое целое число, которое настолько большое, что не может быть записано в компьютере, то применение вышеупомянутых свойств позволяет уменьшить первые два операнда прежде, чем начать умножение. Другими словами, перечисленные свойства позволяют нам работать с меньшими числами. Этот факт станет понятнее при обсуждении экспоненциальных операций в последующих лекциях.

Следующие примеры показывают приложение вышеупомянутых свойств.

Источник

Сравнения, система вычетов, решение линейных систем по модулю

Содержание

Сравнения по модулю [ править ]

Будем рассматривать целые числа в связи с остатками от деления их на данное целое число m, которое назовем модулем. Каждому целому числу отвечает определенный остаток от деления его на m. Если двум целым a и b отвечает один и тот же остаток r, то они называются сравнимыми по модулю m.

Сравнимость для a и b записывается так :
[math]a \equiv b(mod \text < >m)[/math]

Сравнимость чисел a и b по модулю m равносильна:

Арифметика сравнений [ править ]

Свойства сравнений [ править ]

Полная и приведенная система вычетов [ править ]

Числа равноостаточные(сравнимые по модулю m) образуют класс чисел по модулю m. Из такого определения следует, что всем числам класса отвечает один остаток r, и мы получим все числа класса, если в форме [math]mt + r [/math] заставим t пробегать все целые числа. Таким образом для каждого значения остатка имеется свой класс чисел.

Любые m чисел, попарно несравнимые по модулю m, образуют полную систему вычетов по этому модулю.

Согласно 10 свойству сравнений, числа одного класса по модулю m имеют одинаковый НОД. Особенно важны классы, содержащие числа, взаимно простые с модулем. Взяв вычет от каждого такого класса, получим приведенную систему вычетов по модулю m.

Решение линейных систем по модулю [ править ]

Примеры решения [ править ]

Источник

Решить систему в поле вычетов

решите систему уравнений:

в поле вычетов по модулю 5 и по модулю 7. (если нетрудно прокомментируйте чтоб можно было разобраться)

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Решить уравнение № 2 x^2+5x+1=0 в поле вычетов по модулю 11
Решить уравнение в поле вычетов по модулю 11 x^2+5x+1=0

Примитивный элемент в поле вычетов
Здравствуйте. Объясните, пожалуйста, как найти примитивный элемент в поле GF(2^3) или GF(5^3). С.

Решение

Решение

В поле вычетов все ненулевые элементы имеют обратные (по умножению):
.
Думаю понятно, что мы работаем не с числами, а с классами вычетов, поэтому правильно писать
, но для краткости пишем без обозначения классов. Исходя из данных равенств, приводим расширенную матрицу к ступенчатому виду:
1 2 3 | 1
0 0 1 | 1
0 0 0 | 1

Так как ранг расширенной матрицы больше ранга матрицы системы, то по теореме Кронеккера-Капелли в поле решения нет, то есть система несовместна.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Система уравнений в поле вычетов по модулю
Помогите решить систему уравнений: в поле вычетов по модулю 5 и по модулю 7.

Найти ответ в системе уравнений в поле вычетов по модулю 5
Найти ответ в системе уравнений в поле вычетов по модулю 5. 3×1+4×2=1 2×1+x2=2 По методу.

Поле Галуа. Решить систему
необходимо решить в GF(23) систему 2х+2у=3 х+2у=2

решить систему
помогите найти х,у решив систему u=x+y v=1\x+1\y

Источник

Кольцо вычетов

Сравнение по модулю натурального числа — отношение эквивалентности на множестве целых чисел, связанное с делимостью. Оно даёт возможность работать с системой чисел, более простой чем целые числа, в которой значения «зацикливаются» (повторяются) после достижения определенного значения.

В дискретной математике, для сравнений по модулю используется также термин модульная (или модулярная) арифметика.

Содержание

Определения

Утверждение « a и b сравнимы по модулю n » записывается в виде:

Свойства

Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если

Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: , однако, сократив на 2, мы получаем ошибочное сравнение: . Правила сокращения для сравнений следующие.

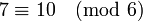
Нельзя также выполнять операции со сравнениями, если их модули не совпадают.

Классы вычетов

Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел , то классы вычетов по модулю n представляют собой классы эквивалентности; их количество равно n. Множество всех классов вычетов по модулю n обозначается или .

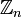
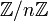
Операции сложения и умножения на индуцируют соответствующие операции на множестве :

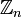
[a]_n + [b]_n = [a + b]_n

Относительно этих операций множество 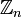является конечным кольцом, а если n простое — конечным полем.

Решение сравнений

Сравнения первой степени

В теории чисел, криптографии и других областях науки часто возникает задача отыскания решений сравнения первой степени вида:

Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:

Практическое вычисление значения c можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:

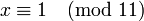
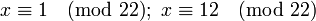
Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11: , эквивалентное двум решениям по модулю 22: .

Сравнения второй степени

Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.

История

В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.

Ссылки

Полезное

Смотреть что такое «Кольцо вычетов» в других словарях:

Кольцо (алгебра) — Кольцо это множество, на котором заданы две операции, «сложение» и «умножение», со свойствами, напоминающими сложение и умножение целых чисел. Содержание 1 Определения 2 Связанные определения 3 Простейшие свойства … Википедия

Кольцо (множество) — Кольцо это множество, на котором заданы две операции, «сложение» и «умножение», со свойствами, напоминающими сложение и умножение целых чисел. Содержание 1 Определения 2 Связанные определения 3 Простейшие свойства … Википедия

Кольцо (математика) — У этого термина существуют и другие значения, см. Кольцо. В абстрактной алгебре кольцо это один из наиболее часто встречающихся видов алгебраической структуры. Простейшими примерами колец являются алгебры чисел (целых, вещественных,… … Википедия

Кольцо алгебраическое — Кольцо алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами К. могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных … Большая советская энциклопедия

Кольцо — алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами К. могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных … Большая советская энциклопедия

Кольцо когомологий — Гомология одно из основных понятий алгебраической топологии. Замкнутая линия гомологична нулю, если она ограничивает кусок поверхности, который отделяется от неё, если мы произведём разрез по этой линии. Например, на сфере любая замкнутая линия… … Википедия

Мультипликативная группа кольца вычетов — Приведённая система вычетов по модулю m множество всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(·) функция Эйлера. В качестве приведённой системы вычетов… … Википедия

АНАЛИТИЧЕСКОЕ КОЛЬЦО — кольцо ростков аналитич. функций в точке аналитического пространства. Более точно: пусть kесть поле с нетривиальным абсолютным значением (обычно предполагаемое полным) и есть fc алгебра степенных рядов от с коэффициентами в k, сходящихся в нек… … Математическая энциклопедия

ЛОКАЛЬНОЕ КОЛЬЦО — коммутативное кольцо с единицей, имеющее единственный максимальный идеал. Если А Л. к. с максимальным идеалом то факторкольцо является полем и наз. полем вычетов Л. к. А. Примеры Л. к. Любое поле или кольцо нормирования является локальным.… … Математическая энциклопедия

ДИСКРЕТНОГО НОРМИРОВАНИЯ КОЛЬЦО — дискретно нормированное кольцо, кольцо с дискретным нормированием, т. е. область целостности с единицей, в к рой существует такой элемент я, что любой ненулевой идеал порождается нек рой степенью элемента я; такой элемент наз. униформизирующим и… … Математическая энциклопедия

Источник

Поле вычетов

Как было показано в разд.1.2.3, полная система вычетов является коммутативным кольцом.

Единицей мультипликативной полугруппы является класс 1, поскольку 1*a=a*1=(1a) mod n=a.

Однако делители нуля не имеют обратных элементов. Действительно, пусть n – составное число и a,b – делители нуля: a*b=b*a=0; a¹0, b¹0; и пусть a имеет обратный элемент c: a*c=c*a=1. Тогда b=b*1=b*(a*c)=(b*a)*c=0*c=0, что противоречит предположению b¹0.

Следовательно, мультипликативная полугруппа не образует группу и полная система вычетов не является полем.

Однако, если ввести ограничение, что n – простое число, то мультипликативная полугруппа без нуля образует коммутативную (абелеву) группу и полная система вычетов будет является полем.

Так как операция умножения на множестве Z_n коммутативна, то для доказательства того, что является полем требуется доказать утверждение: если n – простое число, то для любого aÎ<1,2,…,n-1>, (a¹0), существует bÎ<1,2,…,n-1> (b¹0), такое что a*b=b*a=(ab) mod n =1.

Поскольку a является полем.

В этом случае можно ввести операцию деления, кроме деления на нуль

Источник