поле тонкой заряженной нити
Учебники
Журнал «Квант»
Общие
Теорема Остроградского—Гаусса и ее применение для расчета электростатических полей
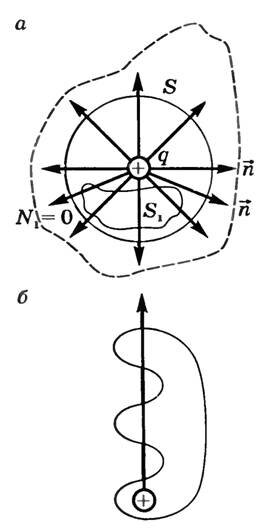
Пусть поле создается точечным электрическим зарядом q. Проведем замкнутую сферическую поверхность площадью S (рис. 2), окружающую этот заряд, центр которой совпадает с точкой нахождения заряда. Вычислим поток вектора напряженности через эту поверхность. За положительное направление нормали выберем направление внешней нормали \(
\vec n\). В этом случае во всех точках сферической поверхности E = const и cos α = 1.
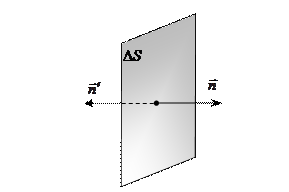
Модуль напряженности поля на расстоянии R от заряда \(
Следовательно, поток вектора напряженности через сферическую поверхность
Полученный результат будет справедлив и для поверхности произвольной формы, а также при любом расположении заряда внутри этой поверхности. Действительно, если окружить сферу произвольной замкнутой поверхностью (рис. 2, а — поверхность изображена штрихами), то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.
Если замкнутая поверхность произвольной формы охватывает заряд (рис. 2, б), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в поверхность, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линии, входящей в поверхность. Если же внутри поверхности площадью S1 (см. рис. 2) заряды отсутствуют, то поток напряженности через эту поверхность равен нулю (NS = 0).
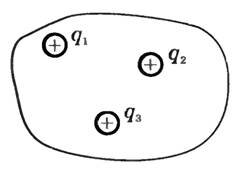
Если рассматриваемая поверхность охватывает не один, а несколько электрических зарядов, то под q следует понимать алгебраическую сумму этих зарядов (рис. 3) и
Эта формула выражает теорему Остроградского—Гаусса: поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на произведение электрической постоянной и диэлектрической проницаемости среды.
Применим эту теорему для расчета электростатических полей некоторых проводников.
Равномерно заряженная бесконечная плоскость
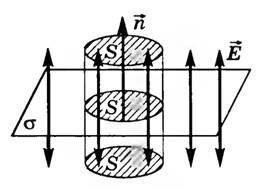
Пусть σ — поверхностная плотность заряда на плоскости (рис. 4).
В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности (α = 90°, cos α = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2ES. Внутри цилиндра заключен заряд q = σS, поэтому, согласно теореме Остроградского-Гаусса, \(
2ES = \frac<\sigma S><\varepsilon_0 \varepsilon>\), где ε = 1 (для вакуума), откуда следует, что напряженность поля равномерно заряженной бесконечной плоскости
Бесконечная равномерно заряженная нить
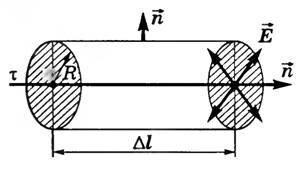
Пусть τ — линейная плотность заряда нити. Выделим участок нити длиной Δl и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью (рис. 5).
Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность \(
N = E \cdot 2 \pi R \Delta l\), где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (α = 90°, cos α = 0). Тогда полный поток напряженности через выделенный цилиндр
Заряд, находящийся внутри этого цилиндра, q = τ · Δl.
Согласно теореме Остроградского—Гаусса, можно записать \(
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 220-222.
Поле тонкой заряженной нити
Пример 8. Напряженность поля тонкой бесконечно длинной заряженной нити (или цилиндра)
Нить можно отнести к тонкой, если ее радиус много меньше расстояния, на котором определяется напряженность, а к бесконечно длинной – если длина нити значительно больше этого расстояния. Найдем напряженность поля равномерно заряженной с линейной плотностью t тонкой бесконечной нити в точке А на расстоянии а от нити. Вспомогательную поверхность, которая должна охватывать заряд, в данном случае удобно выбрать в виде цилиндра радиусом а и длиной l. Ось вспомогательного цилиндра совпадает с нитью. Линии напряженности направлены по радиусам от оси цилиндра, если нить заряжена положительно, и к оси, если заряд нити отрицателен.

Поток вектора напряженности пересекает только цилиндрическую поверхность:

здесь 2 p а × l – площадь боковой поверхности цилиндра. Заряд внутри цилиндра (сосредоточен на отрезке нити, длиной l) в случае, если нить заряжена равномерно, равен Q= t × l. Применяя теорему Гаусса, получим:

Напряженность поля в точке А:

Таким образом, напряженность поля тонкой бесконечной заряженной нити пропорциональна линейной плотности заряда на нити и обратно пропорциональна расстоянию от нити.
Самостоятельно примените теорему Гаусса для нахождения напряженности поля бесконечной заряженной плоскости. Какую здесь следует выбрать вспомогательную поверхность?
Пример 9. Напряженность поля, создаваемого заряженной нитью конечной длины в точке, находящейся от нее на расстоянии, сравнимом с длиной нити.

Оси координат введем так, как показано на рис. 12. Элементарный вектор 






Если взять на нити два симметрично расположенных относительно оси элемента dl1 и dl2, то, как видно из рис. (12,б) dEY1 и dEY2 равны по величине и противоположно направлены, поэтому EY=0, E=EX.
Напряженность поля, создаваемого точечным зарядом dQ в точке А:
Как видно из рис. 12, а:
Положение элемента dl определяется его расстоянием l от перпендикуляра из точки на нить, поэтому:

Возьмем производную от l по a :


Подставив выражения (а), (в), (г) в (б), получим:

Тогда, согласно (в), запишем:


Угол a 1 отсчитывается от перпендикуляра АО вниз (рис.12,а), т.е. является углом отрицательным. Так как функция sin a нечетная, то полученную формулу можно переписать:

Поскольку a 1= a 2, то

(Сравните с выражением для поля, созданного бесконечно длинной нитью).
Заметим, что выражение (е) обращается в бесконечность при а ® 0. Это означает, что понятие тонкой нити справедливо до тех пор, пока рассматриваются точки, расстояния до которых от нити велики по сравнению с ее поперечными размерами.
Поле бесконечно заряженной нити
Рассмотрим бесконечную нить, несущую заряд, равномерно распределённый по её длине. Заряд, сосредоточенный на бесконечно нити, конечно, тоже бесконечен, и поэтому он не может служить количественной характеристикой степени заряженности нити. В качестве такой характеристики принимается «линейная плотность заряда». Эта величина равна заряду, распределённому на отрезке нити единичной длины:

Выясним, какова напряженность поля, создаваемого заряженной нитью на расстоянии а от неё (рис. 1.12).
Для вычисления напряжённости вновь воспользуемся принципом суперпозиции электрических полей и законом Кулона. Выберем на нити элементарный участок dl.На этом участке сосредоточен заряд dq = tdl, который можно считать точечным. В точке А такой заряд создаёт поле (см. 1.3)
Исходя из симметрии задачи, можно заключить, что искомый вектор напряжённости поля 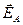
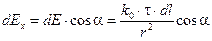
Рис. (1.12 b) позволяет сделать следующие заключения:
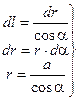
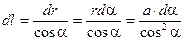
Используя (1.8) и (1.9) в уравнении (1.7), получим
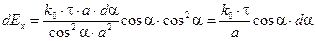
Теперь для решения задачи осталось проинтегрировать (1.10) по всей длине нити. Это означает, что угол a будет меняться от 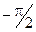
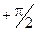
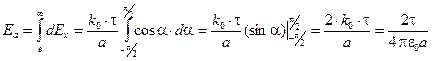
В этой задаче поле обладает цилиндрической симметрией. Напряжённость поля прямо пропорциональна линейной плотности заряда на нити t и обратно пропорциональна расстоянию а от нити до той точки, где измеряется напряжённость.
Лекция 2 «Теорема Гаусса для электрического поля»
Поток вектора напряженности электрического поля.
Теорема Гаусса для электрического поля.
Применение теоремы Гаусса для расчёта электрических полей.
Поле бесконечной заряженной нити.
Поле бесконечной заряженной плоскости. Поле плоского конденсатора.
Поле сферического конденсатора.
Первую лекцию мы закончили расчётом напряжённости полей электрического диполя и бесконечно заряженной нити. В обоих случаях использовался принцип суперпозиции электрических полей. Теперь обратимся ещё к одному методу вычисления напряжённости, основанному на теореме Гаусса для электрического поля. В этой теореме речь идёт о потоке вектора напряжённости через произвольную замкнутую поверхность. Поэтому прежде чем преступить к формулировке и доказательству теоремы, обсудим понятие «поток вектора».
Поток вектора напряжённости электрического поля
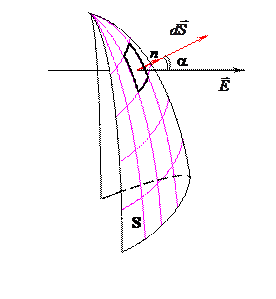
Выделим в однородном электрическом поле плоскую поверхность 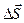
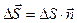
Но единичный нормальный вектор 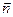
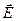
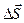
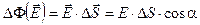
Если поле в общем случае неоднородно, а поверхность S, через которую следует вычислить поток, не плоская, то эту поверхность делят на элементарные участки 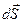
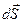
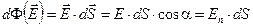
Здесь En = E ∙ cosa — проекция вектора напряжённости на направление нормали 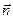
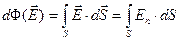
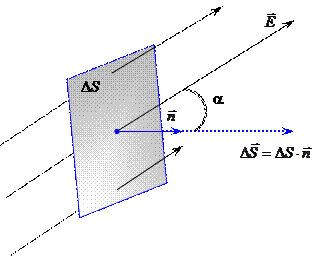
Теперь представим себе замкнутую поверхность в электрическом поле. Для отыскания потока вектора напряжённости через подобную поверхность проделаем следующие операции (рис. 2.4.):
Разделим поверхность на участки 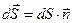
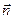
Вычислим поток на каждом элементарном участке 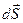
Обратите внимание на то, что вектор 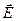
Для вычисления полного потока вектора напряжённости через всю замкнутую поверхность, все эти потоки нужно алгебраически сложить, то есть уравнение (2.3) проинтегрировать по замкнутой поверхности S
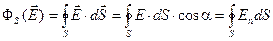
Кружок на знаке интеграл 
Напомним, что при графическом изображении полей, густота силовых линий в произвольной точке поля числено равна значению напряжённости поля в этой точке. Это означает, что

Тогда число силовых линий, пронизывающих поверхность dS, можно записать так
Но ведь это определение потока вектора напряжённости через поверхность dS.
Таким образом, поток вектора напряжённости через поверхность dS численно равен числу силовых линий, пронизывающих эту поверхность (!).
Этот вывод справедлив и для потока электрического поля через замкнутую поверхность: этот поток будет равен алгебраической сумме силовых линий втекающих (–) и вытекающих (+) из замкнутой поверхности.
Теперь обратимся к теореме Гаусса.
Дата добавления: 2015-08-08 ; просмотров: 8475 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Поле тонкой заряженной нити
| Вычисление электрических полей с помощью теоремы Остроградского –Гаусса |   |







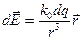
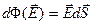



 во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).


 . Следовательно, из теоремы Остроградского–Гаусса получим:
. Следовательно, из теоремы Остроградского–Гаусса получим:
 .
.


 , то
, то , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
, где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
 для боковой поверхности
для боковой поверхности  т.е. зависит от расстояния r.
т.е. зависит от расстояния r.
 на поверхности будет заряд
на поверхности будет заряд  По теореме Остроградского-Гаусса
По теореме Остроградского-Гаусса  , отсюда
, отсюда
 , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
, т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
 ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при
), то можно вблизи поверхности получить поле с очень большой напряженностью и, при  , получить нить.
, получить нить.

 ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).



 ;
;  – объем шара. Тогда по теореме Остроградского-Гаусса запишем:
– объем шара. Тогда по теореме Остроградского-Гаусса запишем: