поле бесконечной заряженной нити
Поле бесконечной заряженной нити
| Вычисление электрических полей с помощью теоремы Остроградского –Гаусса |   |
Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах. Поле бесконечной однородно заряженной плоскости Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле: где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности. Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность Очевидно, что в симметричных, относительно плоскости точках, напряженность Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).
Тогда Суммарный поток через замкнутую поверхность (цилиндр) будет равен: Внутри поверхности заключен заряд откуда видно, что напряженность поля плоскости S равна: Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости Поле двух равномерно заряженных плоскостей Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.13). Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей Тогда внутри плоскостей Вне плоскостей напряженность поля Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор). Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин): Механические силы, действующие между заряженными телами, называют пондермоторными. Тогда сила притяжения между пластинами конденсатора: где S – площадь обкладок конденсатора. Т.к. Это формула для расчета пондермоторной силы. Поле заряженного бесконечно длинного цилиндра (нити) Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра. Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров Следовательно, поток вектора При Если Если уменьшать радиус цилиндра R (при Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае: Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор). Поле заряженного пустотелого шара Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным, Если откуда поле вне сферы: Внутри сферы, при Как видно из (2.5.7) вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы. Поле объемного заряженного шара Для поля вне шара радиусом R (рис. 2.18) получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула: Но внутри шара при где ρ – объемная плотность заряда, равная: Таким образом, внутри шара Поле бесконечно заряженной нитиРассмотрим бесконечную нить, несущую заряд, равномерно распределённый по её длине. Заряд, сосредоточенный на бесконечно нити, конечно, тоже бесконечен, и поэтому он не может служить количественной характеристикой степени заряженности нити. В качестве такой характеристики принимается «линейная плотность заряда». Эта величина равна заряду, распределённому на отрезке нити единичной длины: Выясним, какова напряженность поля, создаваемого заряженной нитью на расстоянии а от неё (рис. 1.12). Для вычисления напряжённости вновь воспользуемся принципом суперпозиции электрических полей и законом Кулона. Выберем на нити элементарный участок dl.На этом участке сосредоточен заряд dq = tdl, который можно считать точечным. В точке А такой заряд создаёт поле (см. 1.3) Исходя из симметрии задачи, можно заключить, что искомый вектор напряжённости поля Рис. (1.12 b) позволяет сделать следующие заключения: Используя (1.8) и (1.9) в уравнении (1.7), получим Теперь для решения задачи осталось проинтегрировать (1.10) по всей длине нити. Это означает, что угол a будет меняться от В этой задаче поле обладает цилиндрической симметрией. Напряжённость поля прямо пропорциональна линейной плотности заряда на нити t и обратно пропорциональна расстоянию а от нити до той точки, где измеряется напряжённость. Лекция 2 «Теорема Гаусса для электрического поля» Поток вектора напряженности электрического поля. Теорема Гаусса для электрического поля. Применение теоремы Гаусса для расчёта электрических полей. Поле бесконечной заряженной нити. Поле бесконечной заряженной плоскости. Поле плоского конденсатора. Поле сферического конденсатора. Первую лекцию мы закончили расчётом напряжённости полей электрического диполя и бесконечно заряженной нити. В обоих случаях использовался принцип суперпозиции электрических полей. Теперь обратимся ещё к одному методу вычисления напряжённости, основанному на теореме Гаусса для электрического поля. В этой теореме речь идёт о потоке вектора напряжённости через произвольную замкнутую поверхность. Поэтому прежде чем преступить к формулировке и доказательству теоремы, обсудим понятие «поток вектора». Поток вектора напряжённости электрического поля Выделим в однородном электрическом поле плоскую поверхность Но единичный нормальный вектор Если поле в общем случае неоднородно, а поверхность S, через которую следует вычислить поток, не плоская, то эту поверхность делят на элементарные участки Здесь En = E ∙ cosa — проекция вектора напряжённости на направление нормали Теперь представим себе замкнутую поверхность в электрическом поле. Для отыскания потока вектора напряжённости через подобную поверхность проделаем следующие операции (рис. 2.4.): Разделим поверхность на участки Вычислим поток на каждом элементарном участке Обратите внимание на то, что вектор Для вычисления полного потока вектора напряжённости через всю замкнутую поверхность, все эти потоки нужно алгебраически сложить, то есть уравнение (2.3) проинтегрировать по замкнутой поверхности S Кружок на знаке интеграл Напомним, что при графическом изображении полей, густота силовых линий в произвольной точке поля числено равна значению напряжённости поля в этой точке. Это означает, что Тогда число силовых линий, пронизывающих поверхность dS, можно записать так Но ведь это определение потока вектора напряжённости через поверхность dS. Таким образом, поток вектора напряжённости через поверхность dS численно равен числу силовых линий, пронизывающих эту поверхность (!). Этот вывод справедлив и для потока электрического поля через замкнутую поверхность: этот поток будет равен алгебраической сумме силовых линий втекающих (–) и вытекающих (+) из замкнутой поверхности. Теперь обратимся к теореме Гаусса. Дата добавления: 2015-08-08 ; просмотров: 8468 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
| ||||


 во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).


 . Следовательно, из теоремы Остроградского–Гаусса получим:
. Следовательно, из теоремы Остроградского–Гаусса получим:
 .
.


 , то
, то , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
, где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
 для боковой поверхности
для боковой поверхности  т.е. зависит от расстояния r.
т.е. зависит от расстояния r.
 на поверхности будет заряд
на поверхности будет заряд  По теореме Остроградского-Гаусса
По теореме Остроградского-Гаусса  , отсюда
, отсюда
 , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
, т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
 ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при
), то можно вблизи поверхности получить поле с очень большой напряженностью и, при  , получить нить.
, получить нить.

 ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).



 ;
;  – объем шара. Тогда по теореме Остроградского-Гаусса запишем:
– объем шара. Тогда по теореме Остроградского-Гаусса запишем:
 .
.
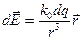
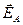 будет направлен по линии, перпендикулярной нити, то есть вдоль оси х. Поэтому сложение векторов напряжённости, можно заменить сложением их проекцией на это направление.
будет направлен по линии, перпендикулярной нити, то есть вдоль оси х. Поэтому сложение векторов напряжённости, можно заменить сложением их проекцией на это направление.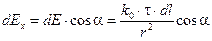 (1.7)
(1.7)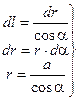 (1.8)
(1.8)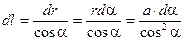 . (1.9)
. (1.9)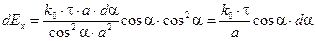 (1.10)
(1.10)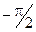 до
до 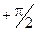 .
.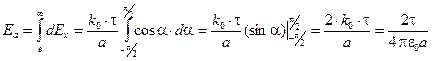 (1.11)
(1.11)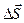 (рис. 2.1.). Эта поверхность — вектор, численно равный площади поверхности DS и направленный перпендикулярно поверхности
(рис. 2.1.). Эта поверхность — вектор, численно равный площади поверхности DS и направленный перпендикулярно поверхности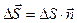 (2.1)
(2.1)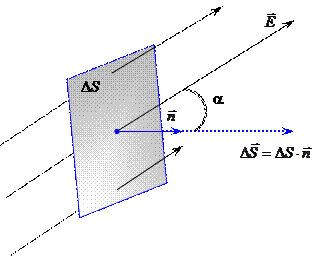
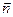 может быть направлен как в одну, так и в другую сторону от поверхности (рис. 2.2.). Произвольно выберем положительное направление нормали так, как это показано на рис. 2.1. По определению потоком вектора напряжённости электрического поля
может быть направлен как в одну, так и в другую сторону от поверхности (рис. 2.2.). Произвольно выберем положительное направление нормали так, как это показано на рис. 2.1. По определению потоком вектора напряжённости электрического поля 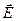 через выделенную поверхность
через выделенную поверхность 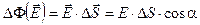 (2.2)
(2.2)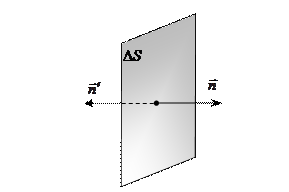
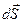 , в пределах которых напряжённость можно считать неизменённой, а сами участки — плоскими (рис. 2.3.) Поток вектора напряжённости через такой элементарный участок
, в пределах которых напряжённость можно считать неизменённой, а сами участки — плоскими (рис. 2.3.) Поток вектора напряжённости через такой элементарный участок 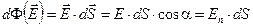 (2.3)
(2.3)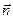 . Полный поток через всю поверхность S найдём, проинтегрировав (2.3) по всей поверхности
. Полный поток через всю поверхность S найдём, проинтегрировав (2.3) по всей поверхности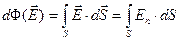 (2.4)
(2.4)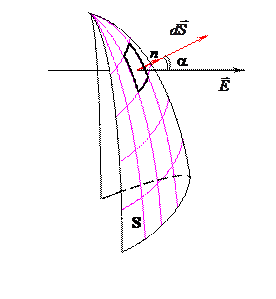
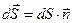 . Важно отметить при этом, что в случае замкнутой поверхности положительной считается только «внешняя» нормаль
. Важно отметить при этом, что в случае замкнутой поверхности положительной считается только «внешняя» нормаль 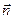 .
.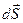 :
: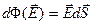
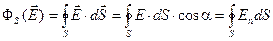 (2.5)
(2.5)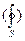 означает, что интегрирование производится по замкнутой поверхности.
означает, что интегрирование производится по замкнутой поверхности.
 .
.