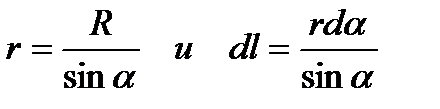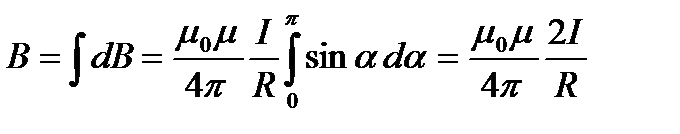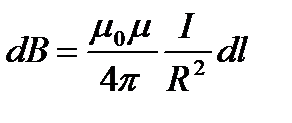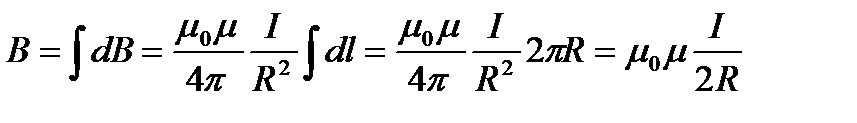поле бесконечно прямого тока

Поле бесконечно прямого тока

Применим закон Био–Савара–Лапласа для расчета магнитных полей простейших токов.

Рассмотрим магнитное поле прямого тока (рис. 1.6).

Все векторы от произвольных элементарных участков имеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей.

Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка 1.6 видно, что:

Подставив найденные значения r и dl в закон Био–Савара–Лапласа, получим:

Для конечного проводника угол α изменяется от , до . Тогда

,

(1.5.1)

Для бесконечно длинного проводника а , тогда

или, что удобнее для расчетов,

,

(1.5.2)

Линии магнитной индукции прямого тока представляют собой систему концентрических окружностей, охватывающих ток (рис. 1.3).

Источник

Теорема Био-Савара-Лапласа. Магнитное поле прямого тока.

Магнитное поле постоянных токов различной формы изучалось учеными Ж. Био и Ф. Саваром. Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.

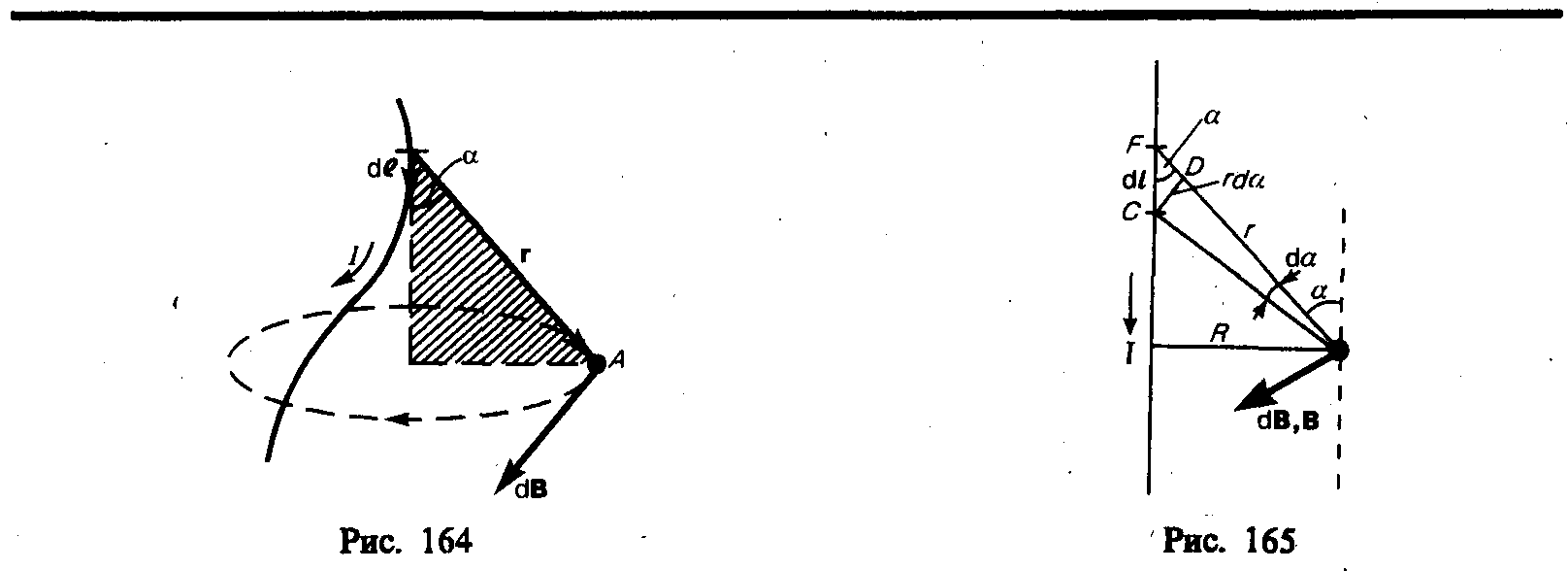
Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде

(110.1)

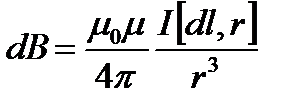
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r—радиус-вектор, проведённый из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление враще­ния головки винта дает направление dB, если поступательное движение винта соответ­ствует направлению тока в элементе.

Модуль вектора dB определяется выражением

, где a — угол между векторами dl и r. (110.2)

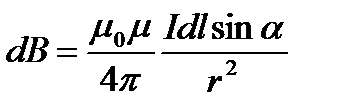
Если распределение тока имеет определенную сим­метрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.

1. Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис.). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к вам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a (угол между векторами dl и r), выразив через него все остальные величины. Из рис. следует, что

(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индук­ция, создаваемая одним элементом проводника, равна 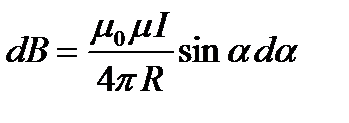(110.4)

Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока 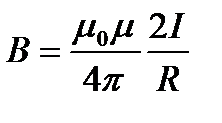(110.5)

2. Магнитное поле в центре кругового проводника с током (рис.). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка. Поэтому сложение век­торов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina =1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),

Следовательно, магнитная индукция поля в центре кругового проводника с током

Источник

Источники магнитного поля

В школьной физике в качестве источников магнитного поля рассматриваются постоянные магниты и проводники с током. Если постоянные магниты мы уже рассмотрели, то с проводниками давайте разберёмся в данном разделе. Простейшие формы проводников для расчёта магнитных полей:

Для каждого из этих проводников можно рассчитать напряжённость магнитного поля в точке.

Итак, движущийся заряд создаёт вокруг себя магнитное поле. Самый простой тип движущегося заряда — это обычный электрический ток. Вопрос только в том, как согнуть проводник:

Рис. 1. Магнитное поле бесконечного проводника

Итак, возьмём бесконечный прямолинейный проводник с током. Слово «бесконечный» в данном случае небольшое приближение. Так для любой точки, находящейся непосредственно вблизи любого линейного проводника, сам проводник «кажется» бесконечным. Пусть по нашему проводнику течёт ток (рис. 1). Прямолинейный проводник с током создаёт вихревое (круговое) магнитное поле вокруг себя. Направление вектора магнитной индукции задаётся правилом буравчика (правилом правой руки). Исходя из этого правила, найдём направление вектора (рис. 2).

Рис. 2. Магнитное поле бесконечного проводника (магнитная индукция)

Для подсчёта модуля вектора магнитной индукции поля вне прямолинейного бесконечного проводника с током можно использовать соотношение (рис. 3):

Рис. 3. Модуль вектора магнитной индукции бесконечного линейного проводника

3D модели рисунков достаточно сложны для рассмотрения, поэтому введены условные обозначения для направлений векторов/токов в трёхмерном пространстве (рис. 4).

Рис. 4. Схематические отображения векторов

Тогда перерисуем рисунок 3, в случае, если мы смотрим сверху провода (рис. 5.1). В этом случае ток течёт на нас, т.е. из рисунка. И в случае, когда мы смотрим на провод снизу вверх (рис. 5.2). В этом случае ток течёт от нас, т.е. внутрь рисунка.

Рис. 5. Поле проводника (вид сверху)

На рисунке 5 точечной линией обозначено магнитное поле прямолинейного тока (оно круговое). Направление вектора магнитной индукции ( ) определяется правилом буравчика (правилом правой руки).

Правило буравчика для прямолинейного тока: правой рукой обхватываем проводник с током, отогнутый большой палец сонаправляем с током, тогда согнутые 4 пальца показывают направление вектора магнитной индукции.

Второй вариант системы, в которой достаточно просто рассчитать модуль вектора магнитной индукции, — это круговой виток с током. Т.е. сам проводник с током представляет собой окружность. По данному проводнику ток может течь как по часовой стрелке (рис. 6.1), так и против часовой (рис. 6.2).

Рис. 6. Круговой виток с током

В целом, магнитное поле такого проводника достаточно сложное, однако для центра витка нахождение модуля вектора магнитной индукции не представляет проблем:

Немного о — относительной магнитной проницаемости среды. Это параметр, который описывает насколько сама среда воспринимает магнитное поле источника. В целом, это табличная величина.

Правило буравчика для кругового тока: обнимаем правой рукой провод, большой отогнутый палец правой руки направляем по току, тогда загнутые 4 пальца будут указывать направление вектора магнитной индукции.

Важно: для наших систем можно запомнить, что прямолинейный ток создаёт круговое магнитное поле (рис.5), а круговой ток создаёт прямолинейное магнитное поле (рис.6).

Вывод: для поиска модуля вектора магнитной индукции достаточно проанализировать систему в задаче и описать её через модель бесконечного прямолинейного или кругового проводника с током.

Источник

6.2. Магнитное поле прямолинейного проводника с током

Вычислим поле, создаваемое током, текущим по тонкому прямолинейному проводу бесконечной длины.

Индукция магнитного поля в произвольной точке А (рис. 6.12), создаваемого элементом проводника dl, будет равна

Рис. 6.12. Магнитное поле прямолинейного проводника

Поля от различных элементов имеют одинаковое направление (по касательной к окружности радиусом R, лежащей в плоскости, ортогональной проводнику). Значит, мы можем складывать (интегрировать) абсолютные величины

Выразим r и sin через переменную интегрирования l

Тогда (6.7) переписывается в виде

Картина силовых линий магнитного поля бесконечно длинного прямолинейного проводника с током представлена на рис. 6.13.

Рис. 6.13. Магнитные силовые линии поля прямолинейного проводника с током:
1 — вид сбоку; 2, 3 — сечение проводника плоскостью, перпендикулярной проводнику

Для обозначения направления тока в проводнике, перпендикулярном плоскости рисунка, будем использовать следующие обозначения (рис. 6.14):

Рис. 6.14. Обозначения направления тока в проводнике

Для обозначения направления тока в проводнике, перпендикулярном плоскости рисунка, будем использовать следующие обозначения (рис. 6.14):

Напомним выражение для напряженности электрического поля тонкой нити, заряженной с линейной плотностью заряда

Сходство выражений очевидно: мы имеем ту же зависимость от расстояния до нити (тока), линейная плотность заряда заменилась на силу тока. Но направления полей различны. Для нити электрическое поле направлено по радиусам. Силовые линии магнитного поля бесконечного прямолинейного проводника с током образуют систему концентрических окружностей, охватывающих проводник. Направления силовых линий образуют с направлением тока правовинтовую систему.

На рис. 6.15 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг прямолинейного проводника с током. Толстый медный проводник пропущен через отверстия в прозрачной пластинке, на которую насыпаны железные опилки. После включения постоянного тока силой 25 А и постукивания по пластинке опилки образуют цепочки, повторяющие форму силовых линий магнитного поля.

Вокруг прямого провода, перпендикулярного пластинке, наблюдаются кольцевые силовые линии, расположенные наиболее густо вблизи провода. При удалении от него поле убывает.

Рис. 6.15. Визуализация силовых линий магнитного поля вокруг прямолинейного проводника

На рис. 6.16 представлены опыты по исследованию распределения силовых линий магнитного поля вокруг проводов, пересекающих картонную пластинку. Железные опилки, насыпанные на пластинку, выстраиваются вдоль силовых линий магнитного поля.

Рис. 6.16. Распределение силовых линий магнитного поля
вблизи пересечения с пластинкой одного, двух и нескольких проводов

Источник

Магнитное поле прямого тока

Вы будете перенаправлены на Автор24

Любой электрический ток можно представить в виде совокупности элементарных токов. Следовательно, можно рассчитать характеристики магнитного поля, порождаемого любыми токами, если использовать:

Закон Био – Савара – Лапласа:

$\vec=\int\limits_l > \left( 2 \right)$.

В выражении (2) следует учитывать, что суммирование является векторным.

Закон Био-Савара-Лапласа дает возможность рассчитывать магнитные поля, которые создают токи, распределенные в пространстве. Плотность этих токов может изменяться в зависимости от координаты (или радиус-вектора, определяющего положение точки) ($\vec(\vec)$).

Результирующее поле находят интегрированием выражения (3) по объему в котором текут токи.

Применение закона Био-Савара – Лапласа для нахождения магнитного поля прямого тока

Рисунок 1. Магнитное поле прямого тока. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Принимая во внимание формулы (5) закон (4) приведем к виду:

Закон полного тока и его применение для нахождения магнитного поля прямого тока

Допустим, что токи, создающие магнитное поле и контур, по которому мы будем рассматривать интегрирование, находятся в однородном магнитоизотропном веществе, тогда закон полного тока (или закон циркуляции вектора магнитной индукции) запишем в виде:

$\oint\limits_L <\vecd\vec=\mu \mu_<0>I\, \left( 8 \right),>$

Теорема о циркуляции (или закон полного тока), в теории магнетизма, играет роль аналогичную теореме Гаусса для вектора напряженности в электростатике. Если в распределении токов имеется симметрия, то этот закон упрощает процедуру поиска вектора магнитной индукции.

$\oint\limits_L <\vecd> \vec=BL=2\pi R B\, \left( 9 \right)$.

$2\pi RB=\mu \mu_<0>I\, \, \left( 10 \right)$,

считая, что проводник находится в вакууме ($\mu=1$), получаем:

Сравнивая формулы (7) и (11), мы видим, что результаты одинаковые.

Магнитное поле прямого тока в проводе, имеющем конечную длину

Рисунок 2. Магнитное поле прямого тока в проводе, имеющем конечную длину. Автор24 — интернет-биржа студенческих работ

Вектор магнитной индукции перпендикулярен плоскости рисунка. Силовые линии – это окружности, как и у бесконечного проводника.

где из рис.2 видно, что:

Если рассматривать бесконечно длинный проводник, как частный случай прямого проводника с током, то следует учесть, что для него:

тогда из (13) следует:

Результат (14) снова совпал с (7) и (11).

Магнитное поле внутри прямого тока

$\oint\limits_L <\vecd> \vec=B 2\pi r\, \left( 16 \right)$.

Из закона полного тока следует, что:

Для бесконечно длинного провода мы видим:

Источник