пол одинацатава это сколько
Значение слова «пол-одиннадцатого»
по̀л-оди́ннадцатого
1. половина одиннадцатого, 10:30, между десятью и одиннадцатью о времени ◆ Большие стрелки на часах ратуши показывают пол-одиннадцатого. В. П. Беляев, «Старая крепость», 1937–1940 г. (цитата из НКРЯ) ◆ ― Пора спать, Толик. Уже пол-одиннадцатого. Иди, ложись, ― уговаривал папа. Гавриил Троепольский, «Белый Бим черное ухо», 1971 г.
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: южноамериканский — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «пол-одиннадцатого»
Предложения со словом «пол-одиннадцатого»
Отправить комментарий
Дополнительно
Предложения со словом «пол-одиннадцатого»
– Смотри-ка, а времени уже пол-одиннадцатого, – удивился он. – А только что было девять.
Я буду вам сигналить в пол-одиннадцатого утром и вечером.
Не на полу же ей спать, да и на часах всего-то пол-одиннадцатого.
Синонимы к слову «пол-одиннадцатого»
Правописание
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
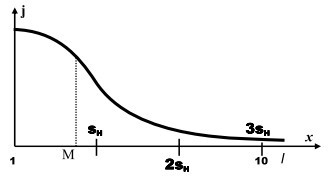
Для начала отметим, что понятие «несколько» применяется к величинам, имеющим очень большой разброс по абсолютной величине. Это могут быть единицы, десятки, тысячи, миллионы штук, или метры, километры, килограммы, тонны. Это могут быть и дробные величины, такие как сантиметры, миллиметры, литры, миллилитры, граммы, миллиграммы и т. д. Поскольку мы пользуемся позиционной системой счисления, то порядок величины может быть вынесен за скобки рассмотрения и служить простым размерным множителем для того отрезка, который мы оцениваем как «несколько». В этом случае удобно воспользоваться логарифмическими представлениями, т. е. использовать логарифмическую шкалу для представления величин. С учётом сказанного, приведём все величины к единому интервалу, базовую величину которого выберем равной основанию (M) используемой позиционной системы счисления. В привычной для нас десятичной системе счисления длина базового интервала будет равна 10 единицам. Он и будет служить нам осью х (смотри рисунок).
Теперь рассмотрим отмеченный выше феномен с инверсией направления изменения верхней границы интервала «несколько» при переходе к миллиону. Человек практически ежедневно и широко пользуется деньгами для покупки товаров и услуг. Наиболее часто он пользуется такими единицами как рубли, десятки и сотни рублей, реже тысячами. Количество людей, пользующихся в своей повседневной практике десятками тысяч рублей и более достаточно мало. Тогда можно проследить следующую тенденцию. Чем выше повседневная потребительская значимость денежной купюры для человека, тем ближе для неё устанавливаются границы значения «несколько» к их математически точному значению. Поскольку миллион для обычного потребителя не является повседневной купюрой, то его повседневная потребительская значимость для человека более абстракция, чем реальность. В этом случаи и границы понятия «несколько» для миллиона устанавливаются скорее как для абстрактного, чем реального объекта, поэтому и оказываются завышенными. А мы-то считали, что ведём опрос на отвлечённых, абстрактных числах и понятиях, а всё свелось подспудно к обыденным денежным знакам, с которыми мы оперируем повседневно. Это следует учитывать при проведении опросов и, особенно, при интерпретации полученных результатов.
Приведённые выше рассуждения о границах понятия «несколько» можно применить к позиционным системам счисления с произвольным основанием. Воспользуемся широко распространённой в вычислительной технике 16-ричной системой счисления. В этом случае длина базового интервала будет равна 16 единицам (от 1 до 16) и поэтому в рассуждениях необходимо использовать логарифмические представления так же по основанию 16. Для функции распределения исходными параметрами будут х0 = 1, sн = 5, тогда математическое ожидание величины «несколько» равно 0,7979sн = 3,9895; дисперсия равна 0,3634(sн)2 = 9,0850; s = 0,6028sн = 3,0140. При переходе от логарифмического к обычному представлению (не забудем, что логарифм берётся по основанию 16), ответ на поставленный в заголовке материала вопрос будет следующим: понятие «несколько» для 16-ричной системы счисления лежит в диапазоне от 2 до 6. Для системы счисления по основанию 8 (ещё одна система счисления, применяемая в вычислительной технике) получим следующий ответ: от 2 до 3.
Таким образом, можно сказать, что понятие «несколько» для:
16-ричной системы счисления лежит в диапазоне от 2 до 6;
10-тичной системы счисления в диапазоне от 2 до 4;
Журнал «Современные наукоемкие технологии» 2009. №4