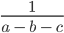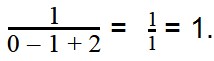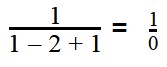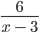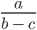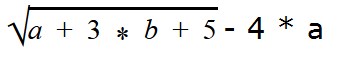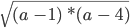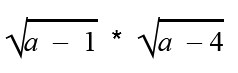Одз или ограничения что писать

ОДЗ. Область допустимых значений (ЕГЭ 2022)

ОДЗ – это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Например, если перед тобой уравнение \( \displaystyle \sqrt=y\), то ни \( \displaystyle x\), ни \( \displaystyle y\) не могут быть отрицательными:

Часто в задачах бывает очень важно учесть ОДЗ и «вычеркнуть» те решения, которые на самом деле решениями не являются.

Иначе ты сделаешь глупую, очень глупую ошибку и не получишь то, что заслужил на ЕГЭ!

Читай эту статью и ты будешь знать об ОДЗ все!

ОДЗ — коротко о главном

ОДЗ – это область допустимых значений, то есть это все значения переменной, при которых выражение имеет смысл.

Функции, для которых важна ОДЗ:

ОДЗ (Область допустимых значений) — подробнее

Давай разберем пример, наглядно показывающий, что такое ОДЗ:

Решим уравнение \( \displaystyle \sqrt<2x+3>=x\).

Все очень просто, если ты уже освоил тему «Иррациональные уравнения».

Возводим левую и правую части уравнения в квадрат:

Теперь решаем квадратное уравнение. Я воспользуюсь теоремой Виета (если забыл, что это такое, – посмотри тему «Квадратные уравнения»).

Вроде все? А давай-ка теперь сделаем проверку – подставим полученные значения в начальное уравнение:

\( \displaystyle x=3:\text< >\sqrt<2\cdot 3+3>=3\text< >\Leftrightarrow \text< >\sqrt<9>=3\) – все верно.

Да потому, что мы не учли ОДЗ!

По определению квадратный корень из любого числа не может быть отрицательным.

Значит, глядя на уравнение \( \displaystyle \sqrt<2x+3>=x\) мы должны сразу же написать:

Если помнишь тему «Иррациональные уравнения», ты сразу скажешь, что второе условие в этой системе писать необязательно. И правда, мы ведь потом возведем все в квадрат, и получится, что \( \displaystyle 2x+3=<^<2>>\), а значит – автоматически неотрицательно.

Итак, с помощью этих рассуждений приходим к такой области допустимых значений:

\( \displaystyle x\ge 0\).

Тогда сразу становится ясно, что корень \( \displaystyle x=-1\) не подходит. И остается единственный ответ \( \displaystyle x=3\).

Всего мы изучаем несколько разных функций, для которых важна ОДЗ. Вот они со своими ОДЗ в удобной табличке.

Источник

ОДЗ или «ограничения»? Как правильно оформлять №15 ЕГЭ по математике

Раньше и трава была зеленее

Всю жизнь все при решении неравенств и уравнений в ЕГЭ по профильной математике писали ОДЗ (Область Допустимых Значений), понимая под этим ограничения, накладываемые на аргумент «непростыми» функциями типа квадратного корня или логарифма. И не было проблем. Пока в сеть не попали разъяснения методиста из Кемеровской области.

За ТАКОЕ точно снизят

Семинар Трушкиной Т.П., методиста из Кемеровской области, наделал много шума. Оказалось, что на ЕГЭ по математике можно получит 0 баллов за задачу, даже имея верный ответ и верную последовательность рассуждений. Все из-за неправильного использования понятия «ОДЗ». Первое, что ясно совершенно точно: если вы выписали «ОДЗ» «не полностью» — прощайтесь с баллами за задачу. Если вы решили выписать лишь ограничения, вносимые логарифмической функцией, а условие отличия знаменателя от нуля оставить на потом («ну они ведь и далее сохранятся, «переход равносилен»»), и назвали эти «неполные» ограничения словом ОДЗ — то это 0 баллов. И можно было даже не браться за задачу =(

Пример неверного оформления

Если хотите пользоваться равносильными переходами — пользуйтесь, никто это не запрещает. Но тогда ОДЗ вам вообще ни к чему — работайте спокойно через систему условий, и будет вам счастье.

Пример верного оформления равносильным переходом, без использования ОДЗ

Скажите детям — пусть они ОДЗ выбросят!

Но даже при правильной, полностью выписанной ОДЗ, есть риск нарваться на неприятности. Эксперт заявляет: в школьных учебниках по математике понятие области допустимых значений (ОДЗ) определен лишь для функций. Поэтому использовать это понятие при решении уравнений и неравенств не рекомендуется. Однако использование ОДЗ в неравенствах и уравнениях активно использовалось преподавателями ВУЗов, в том числе при работе со школьниками, постепенно «мигрировало» в методички и сборники по подготовке к ЕГЭ, и теперь уже прочно укоренилось в умах репетиторов, учителей и абитуриентов. Как показывает практика, полностью выписанные ограничения на переменную под заголовком «ОДЗ» не ведут к снижению баллов на ЕГЭ по профильной математике. Тем не менее, эксперт не рекомендует использовать эту конструкцию.

«Коллеги, лучше вообще ничего не писать; Скажите детям — пусть они ОДЗ выбросят!» — столько эмоций на пустом, казалось бы, месте.

Эксперт рекомендует накладывать ограничения на переменную, при этом никак это не «озаглавливать». При это заголовки типа «ограничения», «условия», «важные замечания» и т.п. возбраняться не должны.

Наша бесплатная Игра-тренажер «ударения на ЕГЭ»

А что говорят интернет-гуру?

Специалисты в области подготовки к ЕГЭ по профильной математике разделились во взглядах. Многие известные Ютуб-блогеры (Борис Трушин, Wild Mathing) придерживаются того мнения, что полностью выписанная ОДЗ ни в коем случае к снижению баллов не приведет. Однако выписаны ограничения, действительно, должны быть полностью. То есть если у вас, например, имеется неравенство с логарифмом, да который ещё и стоит в знаменателе дроби — будьте любезны, потребуйте, чтобы аргумент логарифма был положителен, основание положительно и отлично от единицы, а также чтобы знаменатель вашей дроби был отличен от нуля.

Пример верного и неверного оформления

То, что за верно выписанную ОДЗ вам не снизят баллы, подтверждают и официальные методические рекомендации по оцениванию выполнения заданий с развернутым ответом ЕГЭ по профильной математике от РосОбрНадзора. Ниже приведен пример работы с верно выписанной ОДЗ. Работа оценена на максимальный балл. К ОДЗ никто не придирался.

Пример верно выполненной работы из методички РосОбрНадзора

Если Вам нужна методичка для экспертов по оцениванию работ ЕГЭ по профильной математике — можете написать нам в сообщения сообщества ВК. Подскажем, где скачать.

И как же быть?

А где пруфы?

Ну, если вам мало всего выше написанного — смотрите полную запись вебинара

Источник

Область допустимых значений функции

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении 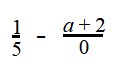— пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Запомните

Например, если х > 6, но х

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

Рассмотрим каждый случай в отдельности.

Пример 7

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 8

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 9

Рассмотрим выражение

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

Источник

Область допустимых значений (ОДЗ): теория, примеры, решения

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Решение

Решение

Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

Рассмотрим на примере.

Рассмотрим пример с наличием подкоренного выражения.

Нужно избегать преобразований, которые сужают ОДЗ.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

При наличии логарифмов дело обстоит немного иначе.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.

Источник

Область допустимых значений

В школьном курсе алгебры есть всего пять элементарных функций, которые имеют ограниченную область определения. Вот они:

1. ОДЗ:

Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.

2. ОДЗ:

Выражение, стоящее в знаменателе дроби, не может быть равно нулю.

3. ОДЗ:

Выражение, стоящее под знаком логарифма, должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.

4. , ОДЗ:

5. Есть две функции, которые содержат «скрытую» дробь:

и

6. ОДЗ:

Таким образом, функции и имеют разную область определения.

Если выражение содержит одну или несколько функций, которые определены на ограниченном множестве значений аргумента, то для того, чтобы найти ОДЗ выражения, нужно учесть все ограничения, которые накладываются этими функциями.

Чтобы найти область допустимых значений выражения, нужно исследовать, присутствуют ли в выражении функции, которые я перечислила выше. И по мере обнаружения этих функций, записывать задаваемые ими ограничения, двигаясь «снаружи» «внутрь».

Найти область определения функции:

Чтобы найти область определения функции, нужно найти область допустимых значений выражения, которое стоит в правой части уравнения функции

Я специально выбрала «страшную», на первый взгляд, функцию, чтобы показать вам, на какие простые операции разбивается процесс нахождения области допустимых значений.

«Просканируем» выражение, стоящее в правой части равенства:

Знаменатель дроби не равен нулю. Записываем:

2. Мы видим в знаменателе логарифм:

Выражение, стоящее под знаком логарифма должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.

3.Мы видим квадратный корень:

Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.

Теперь запишем все ограничения в систему неравенств:

Решение этой системы неравенств посмотрите в ВИДЕУРОКЕ:

Источник