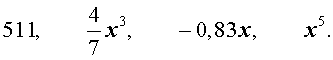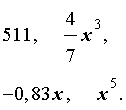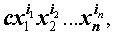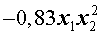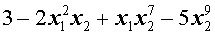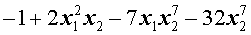Одночлен и многочлен что это

Одночлены и многочлены

Одночлены и многочлены от одной переменной

Если в одночлене степень переменной x не умножена ни на какое число, то считается, что коэффициент одночлена равен 1.

Степень одночлена, являющегося числом, равняется нулю.

Примеры одночленов от переменной x:

Алгебраической суммой одночленов от переменной x называют один или несколько одночленов, соединенных между собой знаками сложения и вычитания. Аналогично определяется алгебраическая сумма чисел.

Алгебраическую сумму одночленов от переменной x также называют многочленом или полиномом от переменной x. Например, многочленом является выражение

Степенью многочлена называют наивысшую степень входящих в него одночленов.

В частности, многочлен

где буквами a и b обозначены произвольные числа, причем число a отлично от нуля, является многочленом первой степени.

Двучленом называется многочлен, состоящий из двух одночленов, трехчленом называется многочлен, состоящий из трех одночленов.

Многочлен всегда можно расположить по возрастанию или по убыванию степеней входящих в него одночленов:

Например, квадратный трехчлен

Одночлены и многочлены от нескольких переменных

Таким образом, одночлен от нескольких переменных является произведением числа на несколько букв, каждая из которых входит в одночлен в целой неотрицательной степени.

Степенью одночлена называют сумму степеней всех входящих в него букв, т.е. сумму целых неотрицательных чисел:

Степенью многочлена от нескольких переменных называют наивысшую степень входящих в него одночленов.

В частности, степень многочлена

Источник

Одночлен и многочлен

Одночленом называется произведение чисел, переменных, степеней переменных.

Примеры: (*)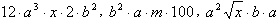

Стандартным видом одночлена называют произведение, в котором на первом месте стоит числовой коэффициент, а произведение одинаковых переменных представлено их степенью.

Стандартный вид одночленов, представленных в примере (*), будет таким:

.

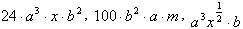
Многочленом (полиномом) – называется сумма одного или нескольких одночленов.

Примеры: .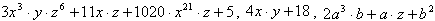

Одночлены, входящие в сумму многочлена называются членами многочлена.

Многочлен, в котором два члена, называют двучленом.

Многочлен, в котором три члена называют трёхчленом.

Подобными членами называются два члена многочлена, в которых показатели степеней при одинаковых переменных равны.

Например, в многочлене 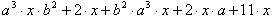подобны между собой первый и третий члены, а так же второй и пятый.

Подобные члены можно заменить одним, сложив их коэффициенты, а буквенную часть, оставив неизменной. Такое преобразование называется приведением подобных. Чтобы облегчить эту процедуру, подобные члены подчёркивают одинаковыми линиями.

Ошибка в тексте? Выдели её мышкой и нажми

Источник

Одночлены и многочлены

Многочлены — важный класс функций. Значение многочлена вычисляется только операциями сложения, вычитания, умножения. При изменении входящей переменной значение многочлена меняется по закону, также описываемому другим многочленом. И подбирая коэффициенты многочлена можно получить график самых разных всевозможных форм. Эти свойства многочленов очень полезны для математиков, инженеров, конструкторов.

Одночлен

Одночлен — это произведение чисел, переменных и их степеней.

2 × x 3 × y — это произведение числа 2, степени переменной x с показателем 3 и переменной y.

7,3 × a 5 × b 4 — произведение числа 7,3, степени переменной a с показателем 5 и степени переменной b с показателем 4.

Все одночлены — это выражения. Значение одночлена зависит от значений входящих в него переменных.

Подобные одночлены

Два одночлена называются подобными, если они состоят из одинаковых переменных, и каждая переменная входит в оба одночлена с одинаковым показателем степени. Вот два подобных одночлена:

2 × x 3 × y
17 × x 3 × y

они состоят из одинаковых переменных x и y и переменная x входит в оба одночлена с показателем степени 3. И переменная y входит в оба одночлена с показателем 1.

Вот ещё одночлены, составленные из одинаковых переменных — a и b.

3 × a 5 b 4
11 × a 4 × b 5
7,3 × a 5 × b 4

Но показатели отличаются — первый и третий одночлены подобны, а со вторым ни первый ни третий — не подобны.

Степень одночлена

Степень одночлена — это сумма показателей степеней всех входящих в него переменных. У одночлена 7,3 × a 5 × b 4 степень 9, а у одночлена 17 × x 3 × y степень 4.

Многочлен

Многочлен — это сумма одночленов. Пример многочлена:

2 × x 4 × y + 5 × x 2 × y 2 + 6 × x × y 2

Степень многочлена

Степень многочлена — это наибольшая из степеней входящих в него одночленов. У многочлена 2 × x 4 × y + 5 × x 2 × y 2 + 6 × x × y 2 степень 5.

Источник

Одночлен и многочлен. Степень одночлена и многочлена. Стандартный вид одночлена и многочлена

Одночленом называется выражение, которое содержит числа, натуральные степени переменных и их произведения и при этом не содержит никаких других действий с этими числами и переменными.

Любой множитель в одночлене называется коэффициентом. Часто коэффициентом называют лишь числовой множитель . Например, коэффициент одночлена –12сx 6 y 5 равен –12. Одночлены называются подобными, если они одинаковы или отличаются лишь коэффициентами. Поэтому, если два или несколько одночленов имеют одинаковые буквы или их степени, они также подобны.

Степенью одночлена называют сумму показателей степеней всех входящих в него переменных. Если одночлен не содержит переменных, то есть является числом, то его степень считают равной нулю.

Например, степень одночлена 8x 3 yz 2 равна 6, одночлена 6x равна 1, степень одночлена –10 равна 0.

Стандартным видом одночлена называется одночлен в виде произведения числового множителя, стоящего на первом месте, и степеней различных переменных. Любой одночлен можно привести к стандартному виду путем перемножения всех переменных и чисел, входящих в него. Приведем пример приведения одночлена к стандартному виду:

Многочленом называется сумма одночленов. Одночлены, из которых составлен многочлен, называют членами многочлена. Так членами многочлена 4x 2 y – 5xy + 3x – 1 являются 4x 2 y, –5xy, 3x и –1.

Если многочлен состоит из двух членов, то его называют двучленом, если из трех – трехчленом. Одночлен считают многочленом, состоящим из одного члена.

В многочлене 7x 3 y 2 – 12 + 4x 2 y – 2y 2 x 3 + 6 члены 7x 3 y 2 и –2y 2 x 3 являются подобными слагаемыми, так как имеют одну и ту же буквенную часть. Подобными являются и слагаемые –12 и 6, не имеющие буквенной части. Подобные слагаемые в многочлене называют подобными членами многочлена, а приведение подобных слагаемых в многочлене – приведением подобных членов многочлена. Приведем для примера подобные члены в многочлене 7x 3 y 2 – 12 + 4x 2 y – 2y 2 x 3 + 6 = 5x 3 y 2 + 4x 2 y – 6.

Многочлен называется многочленом стандартного вида, если каждый его член является одночленом стандартного вида и этот многочлен не содержит подобных слагаемых.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

Для примера, найдем степень многочлена 8x 4 y 2 – 12 + 4x 2 y – 3y 2 x 4 + 6 – 5y 2 x 4 :

8x 4 y 2 – 12 + 4x 2 y – 3y 2 x 4 + 6 – 5y 2 x 4 = 4x 2 y – 6.

Заметим, что в исходный многочлен входят одночлены шестой степени, но при приведении подобных членов все они сократились, и получился многочлен третьей степени, значит и исходный многочлен имеет степень 3!

Источник

Алгебра. 7 класс

Конспект урока

Обобщение и систематизация знаний по теме «Одночлены, многочлены»

Перечень рассматриваемых вопросов:

Числовое выражение – это выражение, состоящее из чисел, знаков математических действий и скобок.

Значение числового выражения – результат выполненных арифметических действий в числовом выражении.

Одночлен – алгебраическое выражение, являющееся произведением букв и чисел.

Множители одночлена – буквы и числа, входящие в состав одночлена.

Подобные одночлены – одночлены, которые состоят из одних и тех же букв, в одинаковых степенях, но с разными или одинаковыми коэффициентами (числовыми множителями).

Многочлен – сумма одночленов.

Каждый одночлен, входящий в многочлен, называют членом многочлена.

Многочлен стандартного вида – это многочлен, все члены которого являются одночленами стандартного вида, среди которых нет подобных членов.

Вынесением за скобки общего множителя многочлена – называют преобразование многочлена в произведение одночлена и многочлена.

Разложением многочлена на множители, называют его преобразование в произведение двух или нескольких многочленов.

Целое выражение – такое алгебраическое выражение, в котором многочлены соединены знаками сложения, вычитания и умножения.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Числовые, буквенные, алгебраические и целые выражения – все эти понятия объединяет общая тема: «Одночлены и многочлены».Сегодня мы вспомним, что такое одночлен и многочлен и какие действия с ними можно выполнять.

Для начала вспомним, что называют числовым выражением.

Числовое выражение – выражение, состоящее из чисел, знаков математических действий и скобок. Если в данных выражениях выполнить все действия, т.е. получить ответ в видедействительного числа, то говорят, что получено значение числового выражения.

25 – (2 + 14 : 7 · 3) – числовое выражение.

17 –значение числового выражения.

Но бывают числовые выражения, которые не имеют смысла.

Выражение 245 : (25 – 12,5 : 0,5) не имеет смысла, т.к. на ноль делить нельзя:

Вспомним, какое выражение называют буквенным.

Буквенное выражение – выражение, состоящее из букв, чисел, знаков математических действий и скобок.

Стоит отметить, что буквенные и числовые выражения называют алгебраическими выражениями.

Если взять два алгебраических выражения и соединить их знаками арифметических действий (сложения, вычитания, умножения или деления), то получится алгебраическое выражение.

(2 +36 : с) + (23 – 58 · 23) – сумма алгебраических выражений.

(2 + 36 : с) – (23 – 58 · 23) – разность алгебраических выражений.

(2 + 36 : с)(23 – 58 · 23) – произведение алгебраических выражений.

(2 + 36 : с) : (23 – 58 · 23) – частное алгебраических выражений.

Вспомним, что такое одночлен и многочлен.

Одночлен – это алгебраическое выражение, являющееся произведением букв и чисел.

Буквы и числа называют множителями одночлена.

Например, 20 · х · с– одночлен.

Сформулируем некоторые свойства одночленов.

1. Два одночлена считаются равными, если они отличаются друг от друга лишь порядком множителей.

2. Два одночлена считаются равными, если один из них получен из другого заменой некоторых его числовых множителей их произведением.

3. Одночлен считается равным нулю, если среди его множителей есть число ноль. Такой одночлен называется нулевым.

Например, 2х · 0с = 0 – нулевой одночлен.

4. Два одночлена считаются равными, если один получен из другого путём опускания множителя 1.

5. Два одночлена считаются равными, если один из них получен из другого заменой произведения множителей, каждый из которых есть одна та же буква, соответствующей степенью этой буквы.

14ас · асх = 14асасх = 14а 2 с 2 х.

6. Если перед одночленом поставить знак «+», то получится одночлен, равный исходному.

7. А если поставить перед одночленом знак «–», то получится одночлен, равный исходному, умноженному на число (-1).

При этом одночлены, которые отличаются лишь знаками, называются противоположными.

Вспомним определение многочлена.

Многочлен – сумма одночленов.

2a 2 bc 3 +ху 4 + 1,2ср – 9

Сформулируем некоторые свойства многочленов.

1. Члены многочлена можно менять местами.

2abc + 3kх = 3kх + 2abc

2. Если прибавить к многочлену ноль, то он не изменится.

3. В многочлене можно приводить подобные члены.

2ас + 4ас + kх – 3kх = (2+4)ас + (1+(-3))kх = 6ас – 2kх

Многочлен и одночлен можно привести к стандартному виду.

Многочлен стандартного вида – это многочлен, все члены которого являются одночленами стандартного вида, среди которых нет подобных членов.

Стандартным видом одночлена называют такой его вид, в котором это произведение числового множителя и натуральных степеней разных переменных.

Вспомним ещё одно понятие – степень многочлена и одночлена.

Степенью многочлена стандартного вида называют наибольшую из степеней одночленов, входящих в этот многочлен.

Степенью одночлена, записанного в стандартном виде, является сумма показателей степеней всех букв, которые входят в его запись.

14a 2 bc 3 + 7kх – многочлен 6 степени.

15х 2 у 3 – одночлен 5 степени.

С многочленами можно выполнять арифметические действия: сложение, вычитание, умножение.

Действия с многочленами.

(6а + х) + (4а – с) = 6а+х+4а – с = 10а + с + х – сумма многочленов.

(6а+х) – (4а – с)= 6а+х – 4а+с= 2а +с +х – разность многочленов.

(6а+х)(4а – с)= 6а∙4а+ 6а∙(-с)+х∙4а+х∙(-с) =24а 2 – 6ас + 4ах – сх – произведение многочленов.

Стоит отметить, что алгебраические выражения называют целыми, если многочлены в нём соединены знаками сложения, вычитания и умножения.

(а + с)(а – х) + 2аk + (4k – х)

Итак, сегодня мы повторили различные виды выражений, вспомнили, что значит стандартный вид многочленов и одночленов. Переходим к тренировочным заданиям.

Докажем следующее тождество:

(х 5 – 1)= (х – 1)(х 4 + х 3 + х 2 + х + 1).

Для доказательства возьмём правую часть равенства, преобразуем её, используя правило умножения многочленов, а затем приведём подобные члены и сравним с левой частью равенства.

(х – 1)(х 4 + х 3 + х 2 + х + 1) = х ∙ х 4 + х ∙ х 3 + х ∙ х 2 + х ∙ х + х ∙ 1 + (-1) ∙ х 4 + (-1) ∙ х 3 + (-1) ∙ х 2 + (-1) ∙ х + (-1) ∙ 1 = х 5 + х 4 + х 3 + х 2 + х – х 4 – х 3 – х 2 – х – 1 = х 5 + (1 – 1)х 4 + (1 – 1)х 3 + (1 – 1)х 2 + (1 – 1)х – 1 = х 5 + 0 ∙ х 4 + 0 ∙ х 3 + 0 ∙ х 2 + 0 ∙ х – 1 = х 5 – 1.

Левая и правая часть равенства равны, что и требовалось доказать.

Разбор заданий тренировочного модуля.

1.Каким алгебраическим выражением определяется периметр пятиугольника со сторонами: а,с, k, х,у?

Нужно вспомнить, что периметр многоугольника – это сумма всех его сторон. По условию нужно найти периметр пятиугольника со сторонами а,с, k, х,у, следовательно, найти сумму всех его сторон: а + с + k + х + у. Это и есть искомый ответ.

Ответ:а + с + k + х + у.

2. Упростите выражение: (2а + 7) (а – 1) + (а – 4) (3а + 2).

Используем правила умножения многочлена на многочлен, после выполнения умножения многочленов, приведём полученное выражение к стандартному виду.

Источник