Одна труба наполняет резервуар на 54 минуты дольше чем вторая
Первая труба наполняет резервуар
Первая труба наполняет резервуар на 54 минуты дольше, чем вторая. Обе трубы наполняют этот же резервуар за 36 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Примем весь резервуар за 1.
Пусть вторая труба наполняет резервуар за x минут, тогда первая труба наполняет его за (x+54) минуты.
Тогда 1 труба наполняет в минуту
части резервуара, вторая — 1/x части резервуара в минуту.
Две трубы вместе наполняют резервуар за 36 минут. Значит, в 1 минуту они наполняют 1/36 части резервуара.
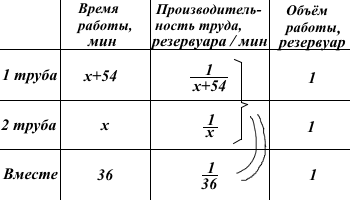
Эти рассуждения можно оформить в виде таблицы:
Составим уравнение и решим его:
x1=54, x2=-36 — не удовлетворяет условию.
Следовательно, вторая труба наполняет резервуар за 54 минуты.
Одна труба наполняет резервуар на 54 минуты дольше чем вторая
Первая труба наполняет резервуар на 5 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 6 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Это задание ещё не решено, приводим решение прототипа.
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Пусть вторая труба наполняет резервуар за x минут, а первая — за x + 6 минут. В одну минуту они наполняют соответственно и
часть резервуара. Поскольку за 4 минуты обе трубы заполняют весь резервуар, за одну минуту они наполняют одну четвертую часть резервуара:
Далее можно решать полученное уравнение. Но можно заметить, что при положительных x функция, находящаяся в левой части уравнения, убывает. Поэтому очевидное решение уравнения — единственно. Поскольку вторая труба заполняет
резервуара в минуту, она заполнит весь резервуар за 6 минут.
Одна труба наполняет резервуар на 54 минуты дольше чем вторая
Первая труба наполняет резервуар на 96 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 14 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Это задание ещё не решено, приводим решение прототипа.
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Пусть вторая труба наполняет резервуар за x минут, а первая — за x + 6 минут. В одну минуту они наполняют соответственно и
часть резервуара. Поскольку за 4 минуты обе трубы заполняют весь резервуар, за одну минуту они наполняют одну четвертую часть резервуара:
Далее можно решать полученное уравнение. Но можно заметить, что при положительных x функция, находящаяся в левой части уравнения, убывает. Поэтому очевидное решение уравнения — единственно. Поскольку вторая труба заполняет
резервуара в минуту, она заполнит весь резервуар за 6 минут.
Одна труба наполняет резервуар на 54 минуты дольше чем вторая
Первая труба наполняет резервуар на 55 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 24 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Это задание ещё не решено, приводим решение прототипа.
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Пусть вторая труба наполняет резервуар за x минут, а первая — за x + 6 минут. В одну минуту они наполняют соответственно и
часть резервуара. Поскольку за 4 минуты обе трубы заполняют весь резервуар, за одну минуту они наполняют одну четвертую часть резервуара:
Далее можно решать полученное уравнение. Но можно заметить, что при положительных x функция, находящаяся в левой части уравнения, убывает. Поэтому очевидное решение уравнения — единственно. Поскольку вторая труба заполняет
резервуара в минуту, она заполнит весь резервуар за 6 минут.
Одна труба наполняет резервуар на 54 минуты дольше чем вторая
Первая труба наполняет резервуар на 90 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 24 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Это задание ещё не решено, приводим решение прототипа.
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Пусть вторая труба наполняет резервуар за x минут, а первая — за x + 6 минут. В одну минуту они наполняют соответственно и
часть резервуара. Поскольку за 4 минуты обе трубы заполняют весь резервуар, за одну минуту они наполняют одну четвертую часть резервуара:
Далее можно решать полученное уравнение. Но можно заметить, что при положительных x функция, находящаяся в левой части уравнения, убывает. Поэтому очевидное решение уравнения — единственно. Поскольку вторая труба заполняет
резервуара в минуту, она заполнит весь резервуар за 6 минут.