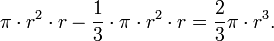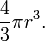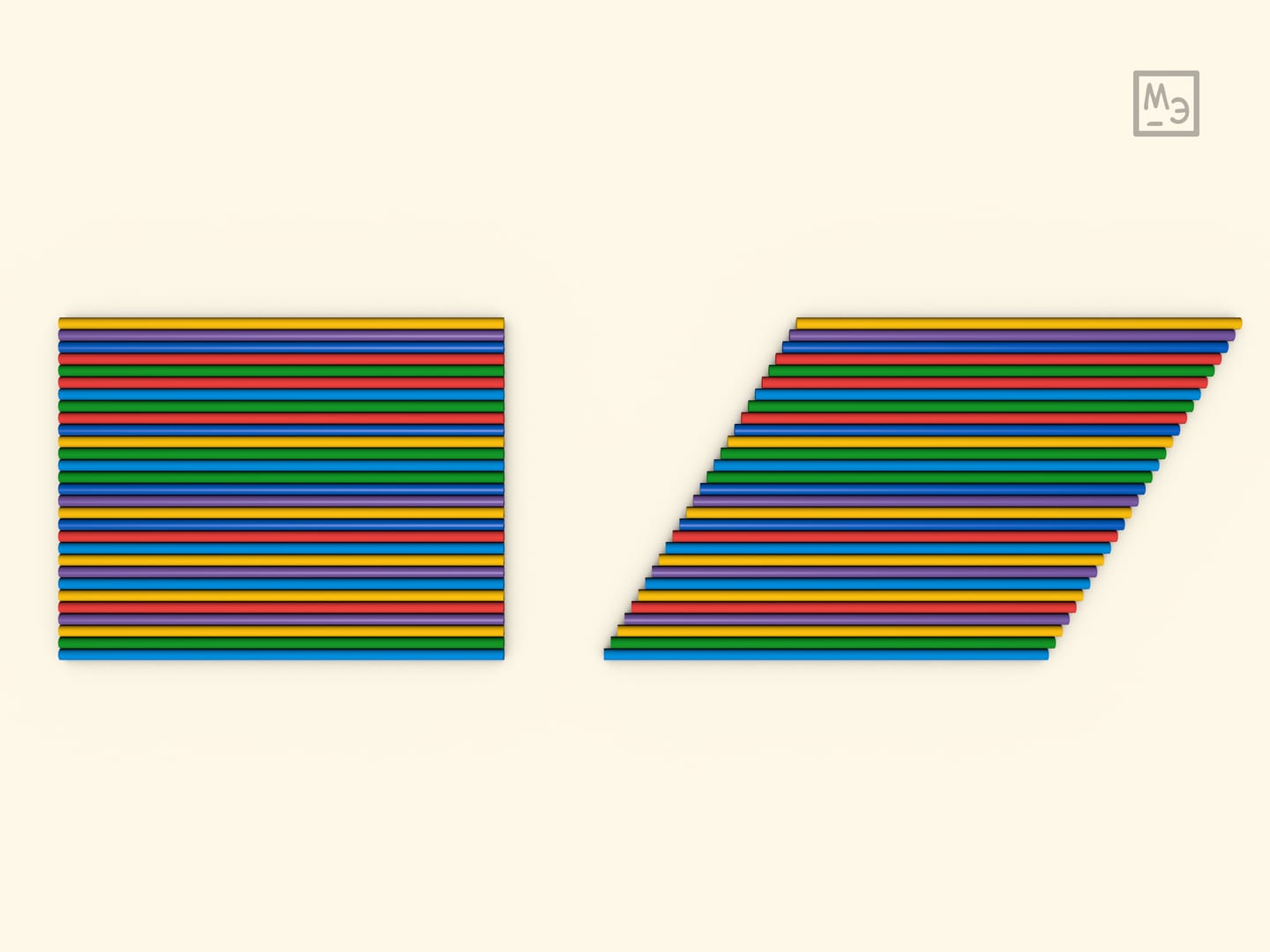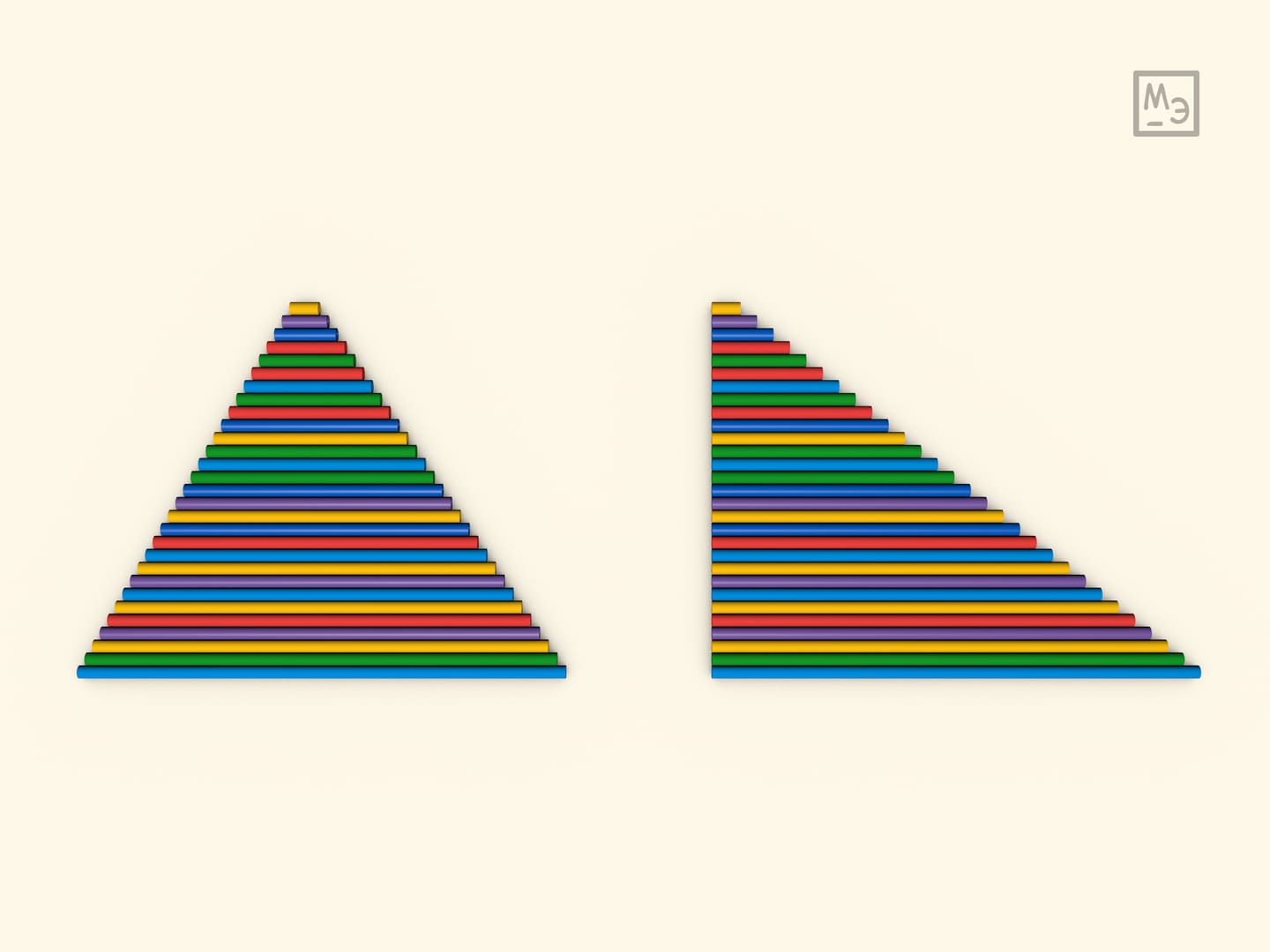Объясните в чем заключается принцип кавальери

Кавальери принцип

Метод неделимых — возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур.

Содержание

Идея метода

Уже Архимед в своих исследованиях рассекал пространственное тело параллельными плоскостями и представлял это тело как своего рода альбом, объединение таких сечений (инфинитезимальное разложение, то есть разложение на бесконечно малые элементы). Здесь возможно влияние атомистов с их «неделимыми». Однако Архимед считал обязательным передоказывать результаты, полученные с помощью метода неделимых, строгим методом исчерпывания. Европейские математики, начиная с XVI века, тоже применяли метод исчерпывания для проведения квадратур (вычисления площадей) и определения центров тяжести.

В XVII веке сразу несколько математиков реализуют идею инфинитезимального разложения плоской фигуры или трёхмерного тела. Среди них Непер, Кеплер, Декарт, Ферма, Кавальери и др. Строго обосновать новый метод они не могли, ссылаясь на то, что результаты получаются правильные, и при желании эти результаты можно доказать громоздким классическим методом. В большинстве случаев это было верно, однако не всегда — например, при вычислении площади неограниченной фигуры метод исчерпывания был неприменим, а новый метод нередко давал верный результат. Классический подход не работал также при суммировании многих рядов и в других случаях работы с бесконечностью.

В труде «Новая астрономия» Кеплер часто использует понятие «неделимых», в том числе при формулировке своих трёх законов движения планет; например, вместо площади он упоминал «сумму радиус-векторов»). В «Новой стереометрии винных бочек» он находит объём множества тел, полученных вращением конических сечений; для нахождения объёма Кеплер разлагает тело в набор сечений и затем собирает этот набор в ином теле, объём которого известен. Большинство его результатов были правильны, хотя несколько ошибок Кеплер всё же допустил.

Галилей был знаком с методом неделимых, однако отчётливо видел его слабые и опасные стороны. В переписке и последних трудах он размышляет о сущности бесконечности, показывает, что бесконечное множество может быть равносчётно своей части, имеющей меньшую меру, так что рассуждения о неделимых плохо обоснованы. Тем не менее он сам фактически использовал неделимые при исследовании равноускоренного движения.

Наиболее ярким и влиятельным представителем «геометрии неделимых» был Кавальери. В его изложении инфинитезимальные представления Кеплера обрели вид общих вычислительных приёмов.

Основанием новой геометрии Кавальери считал следующий тезис:

Фигуры относятся друг к другу, как все их линии, взятые по любой регуле [базе параллельных], а тела — как все их плоскости, взятые по любой регуле.

Отсюда следует, что для нахождения отношения между двумя плоскими или телесными фигурами достаточно найти отношения между всеми неделимыми обеих фигур по какой-либо регуле.

Впоследствии многие учебники геометрии включили в изложение «принцип Кавальери», который он сам формулировал так:

Объемы (или площади) двух фигур равны, если равны между собой площади (или длины) всех соответственных их сечений, проведенных параллельно некоторой данной плоскости (или прямой).

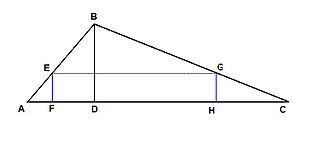
Математики сразу указали на возможность ошибочного применения метода неделимых; один из таких примеров привёл сам Кавальери (см. рисунок). Треугольники ABD и BCD состоят из вертикальных неделимых, причём каждой неделимой левого треугольника (EF) можно взаимно-однозначно сопоставить неделимую той же длины (GH) правого треугольника. Отсюда, согласно принципу Кавальери, следует ошибочный вывод, что площади треугольников равны.

Тем не менее ясного правила для избежания ошибок Кавальери не дал.

Примеры применения метода неделимых

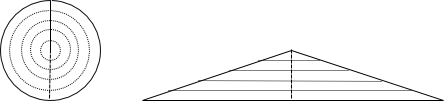
Пример 1. Вычислим площадь круга. Формула для длины окружности: C = 2πR считается известной.

Разобьём круг (слева на рис. 1) на бесконечно малые кольца. Рассмотрим также треугольник (справа на рис. 1) с длиной основания C и высотой R, который тоже разобъём сечениями параллельно основанию. Каждому кольцу радиуса r и длины c = 2πr можно сопоставить одно из сечений треугольника той же длины. Тогда, по принципу Кавальери, их площади равны. А площадь треугольника найти несложно: .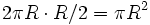

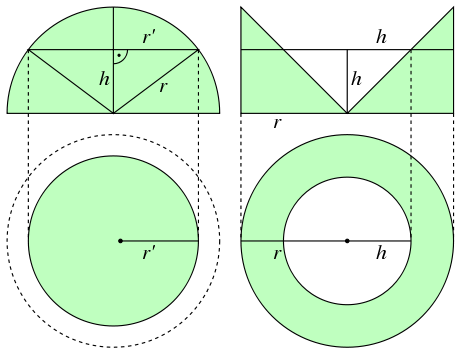
Пример 2. Вычислим объём полушария радиуса r. Формулы для площади круга (пример 1), а также для объёма конуса и цилиндра считаются известными.

Следовательно, по принципу Кавальери, объёмы обоих тел равны. Объём тела справа равен

Вывод: объём полного шара равен

Достижения метода неделимых в XVII веке

Мощь и относительная простота нового метода произвели чрезвычайно сильное впечатление на математиков. Целые поколения, от Валлиса до Лейбница, учились у Кавальери. Торричелли назвал метод неделимых «царской дорогой» в геометрии.

Валлис, ознакомившись с методом Кавальери по книге Торричелли, решил провести его алгебраизацию. Вместо геометрического преобразования сечений он строит в «Арифметике бесконечных» (1656) числовые ряды, которые мы сейчас называем интегральными суммами, и находит эти суммы.

Независимо от Валлиса и лет на 30 раньше эти интегралы вычислили Ферма и Роберваль. В посмертно опубликованном сочинении Ферма виртуозно применяет такие приёмы, как интегрирование по частям и замена переменных, что позволило ему вычислить множество сложных интегралов от дробно-рациональных функций и от многочленов с дробными степенями. Мемуар Ферма почти полностью покрывает результаты Кавальери, но при этом существенно компактнее и понятнее.

Кроме того, интегральные суммы оказались применимы к задачам, недоступным для метода Кавальери — например, спрямление (измерение дуги) кривой. Роберваль исследовал спираль Архимеда, Ферма и Торричелли — параболы и спирали высших порядков. Кристофер Рен спрямил циклоиду.

Декарт использовал инфинитезимальные методы в своей «Оптике», но в целом старался не углубляться в эту область. В трактате «Геометрия» он высказал мнение, что спрямление алгебраических линий невозможно. Это утверждение было опровергнуто лишь через двадцать лет: в 1650-х гг. сразу четыре математика, включая Ферма и Гюйгенса, дали спрямление полукубической параболы. Впрочем, и сам Декарт успешно спрямил, правда, не алгебраическую, а трансцендентную кривую — логарифмическую спираль, длина дуги которой, считая от полюса, пропорциональна радиус-вектору конца дуги — свойство, которое знал и Торричелли.

Идея Валлиса — алгебраизация метода бесконечно малых — достигла высшего развития после открытия математического анализа Ньютоном и Лейбницем. Однако ещё более века, до работ Коши, обоснование анализа бесконечно малых было столь же неубедительным, как и у метода неделимых.

Литература

Полезное

Смотреть что такое «Кавальери принцип» в других словарях:

Кавальери принцип — состоит в следующем: если при пересечении двух тел любой плоскостью, параллельной некоторой заданной плоскости, получаются сечения равной площади, то объёмы тел равны между собой. Это положение (и аналогичное ему для случая плоских фигур) … Большая советская энциклопедия

КАВАЛЬЕРИ ПРИНЦИП — объемы (или площади) двух тел (фигур) равны, если равны между собой площади (длины) соответствующих сечений, проведенных параллельно нек рой данной плоскости (прямой). Это положение, известное еще древнегреческим математикам, наз. обычно К. п.,… … Математическая энциклопедия

Принцип Кавальери — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Содержание 1 Идея метода 2 Примеры применения метода неделимых … Википедия

ПЛОЩАДЬ — численная характеристика, приписываемая плоским фигурам определенного класса (напр., многоугольникам) и обладающая следующими свойствами: 1) П. неотрицательна; 2) П. аддитивна (в случае многоугольников это означает, что если фигура составлена из… … Математическая энциклопедия

Объём — одна из основных величин, связанных с геометрическими телами. В простейших случаях измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Задача вычисления О. простейших тел, идущая от… … Большая советская энциклопедия

Равновеликие и равносоставленные фигуры — Равновеликие фигуры плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие… … Большая советская энциклопедия

Метод неделимых — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Формализация этих приёмов во многом определила развитие интегрального исчисления. Содержание 1 Идея… … Википедия

Неделимых метод — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Содержание 1 Идея метода 2 Примеры применения метода неделимых … Википедия

История математики — История науки … Википедия

Математика Древнего Востока — История науки По тематике Математика Естественные науки … Википедия

Источник

Принцип Кавальери ⁠

Принцип Кава­льери (итал. Bonaventura Francesco Cavalieri, лат. Cavalerius, 1598—1647) поз­во­ляет под­счи­ты­вать площади фигур и объёмы тел, срав­ни­вая дан­ные фигуры и тела с более про­стыми, площади и объёмы кото­рых известны. Суть принципа Кава­льери поз­во­ляет, как это и было в исто­рии чело­ве­че­ства, инту­и­тивно под­ступиться к интеграль­ному исчис­ле­нию: пред­ста­вить площадь как сумму длин отрез­ков, а объём — как сумму площа­дей.

В слу­чае фигур на плос­ко­сти для пер­вого зна­ком­ства с принци­пом Кава­льери можно исполь­зо­вать под­ставку под тарелки, сде­лан­ную по принципу пле­тё­ной циновки. В тех под­став­ках, кото­рые не обшиты по периметру тка­нью, отрезки могут сдвигаться друг отно­си­тельно друга, оста­ва­ясь все­гда парал­лель­ными. Во всех положе­ниях площадь под­ставки оста­ётся одной и той же.

После пер­вого зна­ком­ства на этой же модели полезно разо­брать и пара­докс, при­ве­ден­ный в письме Кава­льери к Тор­ри­челли: ведь на самом деле при сдвиге циновки рас­сто­я­ние между отрез­ками меня­ется, а так можно «дока­зать» равен­ство площа­дей нерав­но­ве­ли­ких тре­уголь­ни­ков.

Другим удоб­ным под­спо­рьем для демон­страции принципа Кава­льери могут стать тру­бочки для напит­ков. Их несложно обре­зать, напри­мер, «под тре­уголь­ник»; можно при жела­нии соеди­нить лес­кой.

В трёхмер­ном про­стран­стве принцип Кава­льери можно про­де­мон­стри­ро­вать на оди­на­ко­вых моне­тах или стопке оди­на­ко­вых кар­то­нок (напри­мер, опять же, под­ста­вок под чашку/бокал). Если кар­тонки круг­лые, то их можно сложить в цилиндр, если прямо­уголь­ные — в парал­ле­лепипед. В обоих слу­чаях объём легко вычис­ля­ется. Тело, полу­чен­ное сдвигом кар­то­нок отно­си­тельно друг друга, выгля­дит более слож­ным, но объём его совпа­дает с объёмом исход­ного.

Источник

Принцип Кавальери

Метод неделимых — возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур.

Содержание

Идея метода

Уже Архимед в своих исследованиях рассекал пространственное тело параллельными плоскостями и представлял это тело как своего рода альбом, объединение таких сечений (инфинитезимальное разложение, то есть разложение на бесконечно малые элементы). Здесь возможно влияние атомистов с их «неделимыми». Однако Архимед считал обязательным передоказывать результаты, полученные с помощью метода неделимых, строгим методом исчерпывания. Европейские математики, начиная с XVI века, тоже применяли метод исчерпывания для проведения квадратур (вычисления площадей) и определения центров тяжести.

В XVII веке сразу несколько математиков реализуют идею инфинитезимального разложения плоской фигуры или трёхмерного тела. Среди них Непер, Кеплер, Декарт, Ферма, Кавальери и др. Строго обосновать новый метод они не могли, ссылаясь на то, что результаты получаются правильные, и при желании эти результаты можно доказать громоздким классическим методом. В большинстве случаев это было верно, однако не всегда — например, при вычислении площади неограниченной фигуры метод исчерпывания был неприменим, а новый метод нередко давал верный результат. Классический подход не работал также при суммировании многих рядов и в других случаях работы с бесконечностью.

В труде «Новая астрономия» Кеплер часто использует понятие «неделимых», в том числе при формулировке своих трёх законов движения планет; например, вместо площади он упоминал «сумму радиус-векторов»). В «Новой стереометрии винных бочек» он находит объём множества тел, полученных вращением конических сечений; для нахождения объёма Кеплер разлагает тело в набор сечений и затем собирает этот набор в ином теле, объём которого известен. Большинство его результатов были правильны, хотя несколько ошибок Кеплер всё же допустил.

Галилей был знаком с методом неделимых, однако отчётливо видел его слабые и опасные стороны. В переписке и последних трудах он размышляет о сущности бесконечности, показывает, что бесконечное множество может быть равносчётно своей части, имеющей меньшую меру, так что рассуждения о неделимых плохо обоснованы. Тем не менее он сам фактически использовал неделимые при исследовании равноускоренного движения.

Наиболее ярким и влиятельным представителем «геометрии неделимых» был Кавальери. В его изложении инфинитезимальные представления Кеплера обрели вид общих вычислительных приёмов.

Основанием новой геометрии Кавальери считал следующий тезис:

Фигуры относятся друг к другу, как все их линии, взятые по любой регуле [базе параллельных], а тела — как все их плоскости, взятые по любой регуле.

Отсюда следует, что для нахождения отношения между двумя плоскими или телесными фигурами достаточно найти отношения между всеми неделимыми обеих фигур по какой-либо регуле.

Впоследствии многие учебники геометрии включили в изложение «принцип Кавальери», который он сам формулировал так:

Объемы (или площади) двух фигур равны, если равны между собой площади (или длины) всех соответственных их сечений, проведенных параллельно некоторой данной плоскости (или прямой).

Математики сразу указали на возможность ошибочного применения метода неделимых; один из таких примеров привёл сам Кавальери (см. рисунок). Треугольники ABD и BCD состоят из вертикальных неделимых, причём каждой неделимой левого треугольника (EF) можно взаимно-однозначно сопоставить неделимую той же длины (GH) правого треугольника. Отсюда, согласно принципу Кавальери, следует ошибочный вывод, что площади треугольников равны.

Тем не менее ясного правила для избежания ошибок Кавальери не дал.

Примеры применения метода неделимых

Пример 1. Вычислим площадь круга. Формула для длины окружности: C = 2πR считается известной.

Разобьём круг (слева на рис. 1) на бесконечно малые кольца. Рассмотрим также треугольник (справа на рис. 1) с длиной основания C и высотой R, который тоже разобъём сечениями параллельно основанию. Каждому кольцу радиуса r и длины c = 2πr можно сопоставить одно из сечений треугольника той же длины. Тогда, по принципу Кавальери, их площади равны. А площадь треугольника найти несложно: .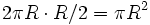

Пример 2. Вычислим объём полушария радиуса r. Формулы для площади круга (пример 1), а также для объёма конуса и цилиндра считаются известными.

Следовательно, по принципу Кавальери, объёмы обоих тел равны. Объём тела справа равен

Вывод: объём полного шара равен

Достижения метода неделимых в XVII веке

Мощь и относительная простота нового метода произвели чрезвычайно сильное впечатление на математиков. Целые поколения, от Валлиса до Лейбница, учились у Кавальери. Торричелли назвал метод неделимых «царской дорогой» в геометрии.

Валлис, ознакомившись с методом Кавальери по книге Торричелли, решил провести его алгебраизацию. Вместо геометрического преобразования сечений он строит в «Арифметике бесконечных» (1656) числовые ряды, которые мы сейчас называем интегральными суммами, и находит эти суммы.

Независимо от Валлиса и лет на 30 раньше эти интегралы вычислили Ферма и Роберваль. В посмертно опубликованном сочинении Ферма виртуозно применяет такие приёмы, как интегрирование по частям и замена переменных, что позволило ему вычислить множество сложных интегралов от дробно-рациональных функций и от многочленов с дробными степенями. Мемуар Ферма почти полностью покрывает результаты Кавальери, но при этом существенно компактнее и понятнее.

Кроме того, интегральные суммы оказались применимы к задачам, недоступным для метода Кавальери — например, спрямление (измерение дуги) кривой. Роберваль исследовал спираль Архимеда, Ферма и Торричелли — параболы и спирали высших порядков. Кристофер Рен спрямил циклоиду.

Декарт использовал инфинитезимальные методы в своей «Оптике», но в целом старался не углубляться в эту область. В трактате «Геометрия» он высказал мнение, что спрямление алгебраических линий невозможно. Это утверждение было опровергнуто лишь через двадцать лет: в 1650-х гг. сразу четыре математика, включая Ферма и Гюйгенса, дали спрямление полукубической параболы. Впрочем, и сам Декарт успешно спрямил, правда, не алгебраическую, а трансцендентную кривую — логарифмическую спираль, длина дуги которой, считая от полюса, пропорциональна радиус-вектору конца дуги — свойство, которое знал и Торричелли.

Идея Валлиса — алгебраизация метода бесконечно малых — достигла высшего развития после открытия математического анализа Ньютоном и Лейбницем. Однако ещё более века, до работ Коши, обоснование анализа бесконечно малых было столь же неубедительным, как и у метода неделимых.

Литература

Полезное

Смотреть что такое «Принцип Кавальери» в других словарях:

Кавальери принцип — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Содержание 1 Идея метода 2 Примеры применения метода неделимых … Википедия

Кавальери принцип — состоит в следующем: если при пересечении двух тел любой плоскостью, параллельной некоторой заданной плоскости, получаются сечения равной площади, то объёмы тел равны между собой. Это положение (и аналогичное ему для случая плоских фигур) … Большая советская энциклопедия

КАВАЛЬЕРИ ПРИНЦИП — объемы (или площади) двух тел (фигур) равны, если равны между собой площади (длины) соответствующих сечений, проведенных параллельно нек рой данной плоскости (прямой). Это положение, известное еще древнегреческим математикам, наз. обычно К. п.,… … Математическая энциклопедия

Метод неделимых — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Формализация этих приёмов во многом определила развитие интегрального исчисления. Содержание 1 Идея… … Википедия

Неделимых метод — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Содержание 1 Идея метода 2 Примеры применения метода неделимых … Википедия

ОБЪЕМ — трехмерного тела числовая характеристика тела, равная в простейшем случае, когда тело можно разбить на конечное множество единичных кубов (т. е. кубов с ребрами длины единица), числу этих кубов. О. трехмерных тел (т. е. множеств трехмерного… … Математическая энциклопедия

ПЛОЩАДЬ — численная характеристика, приписываемая плоским фигурам определенного класса (напр., многоугольникам) и обладающая следующими свойствами: 1) П. неотрицательна; 2) П. аддитивна (в случае многоугольников это означает, что если фигура составлена из… … Математическая энциклопедия

История математики — История науки … Википедия

Математика Древнего Востока — История науки По тематике Математика Естественные науки … Википедия

Ньютон Исаак — Система мира, методология и философия в творчестве Исаака Ньютона Философское значение творчества Ньютона Галилей умер 8 января 1642 г. В том же 1642 г. на Рождество, в Вулсторпе, в окрестностях деревни Колстерворт, Линкольншир, родился Исаак … Западная философия от истоков до наших дней

Источник

Принцип Кавальери

Принцип Кавальери — Если любая плоскость, параллельная данной, пересекает два тела по фигурам равной площади, то объемы этих тел равны.

В XVII в. началась эпоха интегрального исчисления. Математики возвращались к задачам о вычислении площадей криволинейных фигур и объемов «кривых» тел, которыми так успешно занимался в древности Архимед.

Интересовался этим вопросом и итальянский монах Бонавентура Кавальери (1598-1647). Он занимал кафедру математики в Болонском университете. В переписке с астрономом и математиком Г. Галилеем они обсуждали разнообразные механические и математические проблемы, и в частности метод «неделимых». Галилей собирался, но так и не написал книгу об этом методе. В 1635 г. вышла книга Кавальери «Геометрия, изложенная новым способом при помощи неделимых частей непрерывных величин».

При вычислении площадей многоугольников бывает полезно преобразовывать фигуры, не меняя их площадей, например разрезать на части и составлять новые (см. Равносоставленные и равновеликие фигуры). Так можно преобразовать друг в друга треугольники с равными основаниями и высотами.

Интегральное исчисление содержит общие методы для вычисления площадей и объемов, причем там, где применение принципа Кавальери требовало нестандартных построений, к успеху приводят стандартные вычисления, и постепенно принцип Кавальери отошел в область истории. Однако, поскольку по принципу Кавальери легко вычисляются все «школьные» объемы и площади, неоднократно предлагалось принять принцип Кавальери в школьной геометрии за аксиому. Этот материал можно найти в школьных учебниках.

Источник

Кавальери принцип

Смотреть что такое «Кавальери принцип» в других словарях:

Кавальери принцип — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Содержание 1 Идея метода 2 Примеры применения метода неделимых … Википедия

КАВАЛЬЕРИ ПРИНЦИП — объемы (или площади) двух тел (фигур) равны, если равны между собой площади (длины) соответствующих сечений, проведенных параллельно нек рой данной плоскости (прямой). Это положение, известное еще древнегреческим математикам, наз. обычно К. п.,… … Математическая энциклопедия

Принцип Кавальери — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Содержание 1 Идея метода 2 Примеры применения метода неделимых … Википедия

ПЛОЩАДЬ — численная характеристика, приписываемая плоским фигурам определенного класса (напр., многоугольникам) и обладающая следующими свойствами: 1) П. неотрицательна; 2) П. аддитивна (в случае многоугольников это означает, что если фигура составлена из… … Математическая энциклопедия

Объём — одна из основных величин, связанных с геометрическими телами. В простейших случаях измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Задача вычисления О. простейших тел, идущая от… … Большая советская энциклопедия

Равновеликие и равносоставленные фигуры — Равновеликие фигуры плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие… … Большая советская энциклопедия

Метод неделимых — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Формализация этих приёмов во многом определила развитие интегрального исчисления. Содержание 1 Идея… … Википедия

Неделимых метод — Метод неделимых возникшее в конце XVI в. наименование совокупности довольно разнородных приёмов вычисления площадей или объёмов фигур. Содержание 1 Идея метода 2 Примеры применения метода неделимых … Википедия

История математики — История науки … Википедия

Математика Древнего Востока — История науки По тематике Математика Естественные науки … Википедия

Источник