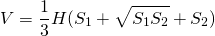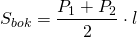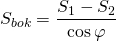Объясните что такое усеченная пирамида

Что такое усеченная пирамида? Свойства и формулы. Пирамиды индейцев майя

Одним из симметричных полиэдров, свойства которого изучает стереометрия, является пирамида. В данной статье рассмотрим подробнее следующие вопросы: что такое пирамида усеченная, как ее можно получить и какими свойствами она характеризуется.

Полная пирамида

Прежде чем раскрывать вопрос, что такое пирамида усеченная, следует дать определение пирамиды в общем случае.

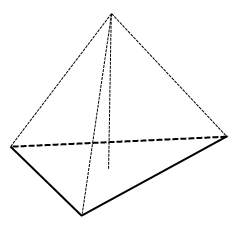
Под пирамидой в геометрии понимают фигуру в трехмерном пространстве, которая состоит из n треугольных граней и одной n-угольной стороны, которая называется основанием. Представить себе пирамиду достаточно просто: необходимо мысленно соединить все углы n-угольника с некоторой одной точкой в пространстве. Рисунок ниже показывает фигуру, которая при этом получается.

Вам будет интересно: Школа №2086: отзывы учеников и родителей, адрес, условия поступления и учебная программа

Здесь мы видим, что углы четырехугольного основания соединены отрезками с одной точкой, которая называется вершиной пирамиды. Боковая поверхность фигуры образована четырьмя разными треугольниками.

Если все треугольники боковой поверхности будут одинаковыми и равнобедренными, то такая фигура называется прямой пирамидой. Если к тому же основание будет представлять правильный n-угольник, например, квадрат, то говорят о пирамиде правильной.

Усеченная пирамида

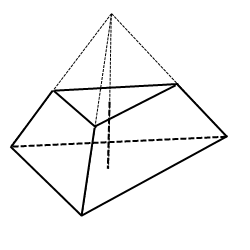
Рассмотренная выше фигура называется полной пирамидой. Теперь покажем, что такое усеченная пирамида и как ее можно получить из полной.

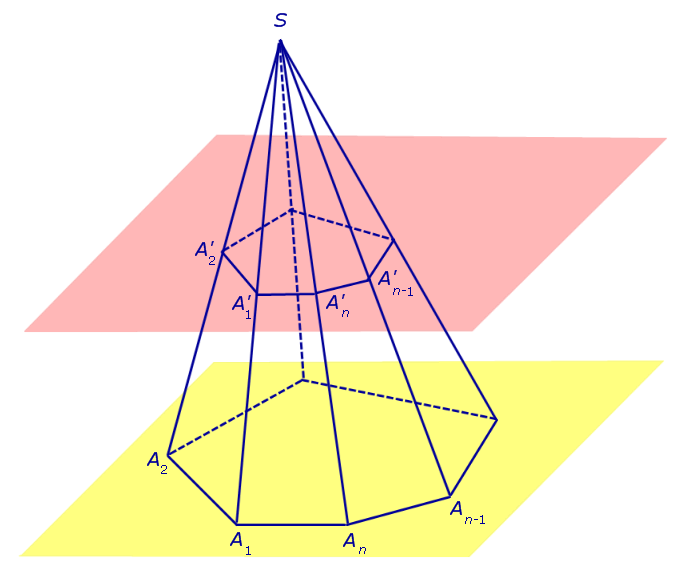
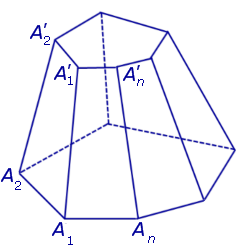
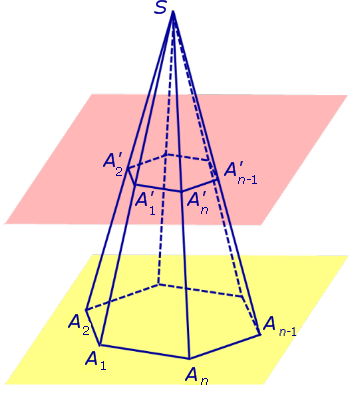
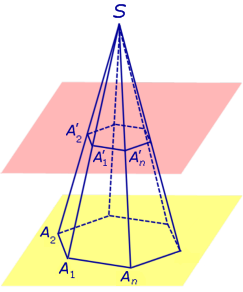
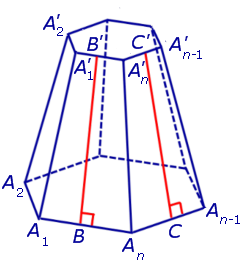
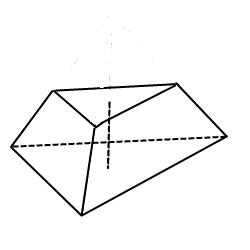
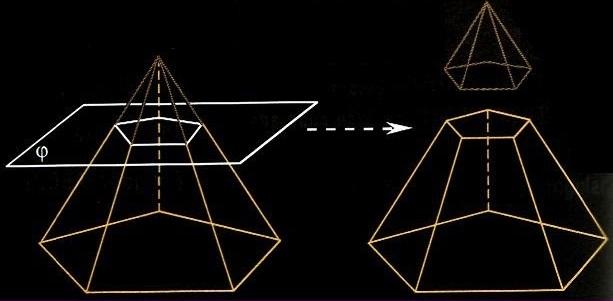
Пусть у нас имеется полная фигура с пятиугольным основанием. Она показана ниже на рисунке слева.

Заметим, что в данном случае мы выбрали секущую плоскость, которая параллельна основанию исходной фигуры. Полученная из правильной фигуры с помощью параллельного сечения усеченная пирамида также будет называться правильной.

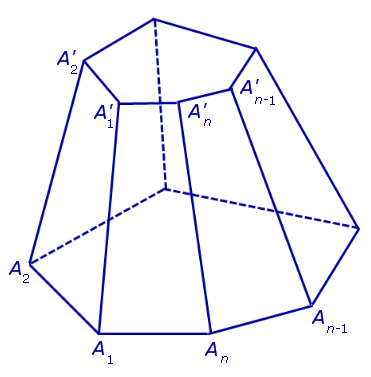
Рисунок также показывает, что основания усеченной пирамиды (пятиугольники в примере) образованы подобными правильными многоугольниками, при этом размер верхнего будет всегда меньше, чем нижнего. Боковая поверхность этой фигуры, в отличие от полной пирамиды, образована равнобедренными трапециями.

Если в основании усеченной пирамиды лежит n-угольник, тогда она имеет 2 × n вершин, 3 × n ребер и n + 2 стороны.

Двумя важными геометрическими параметрами рассматриваемой фигуры являются площадь ее поверхности и объем.

Поверхность пирамиды усеченной

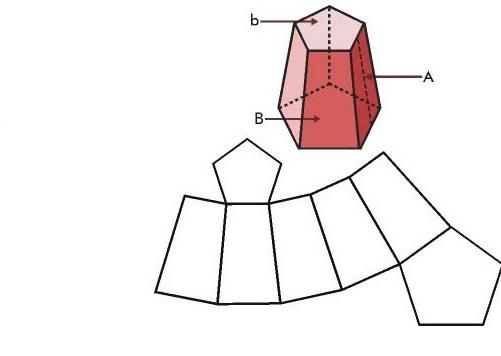
Рассмотрев, что такое усеченная пирамида, перейдем к изучению ее поверхности. Под последней понимают совокупность всех граней, образующих фигуру. Проще всего свойства поверхности изучать на примере развертки. Рисунок ниже показывает развертку для пирамиды с пятиугольными основаниями.

Чтобы вычислить площадь всей ее поверхности, необходимо сложить площадь двух оснований и площадь всех трапеций. Соответствующая формула имеет вид:

S = So1 + So2 + 1/2 × (Po1 + Po2) × Ap.

Например, для случая с четырехугольной правильной усеченной пирамидой эта формула перепишется в виде:

S4 = B2 + b2 + 2 × (B + b ) × Ap.

Объем усеченной пирамиды

Для определения объема рассматриваемой фигуры необходимо знать ее высоту h, а также площади обоих оснований So1 и So2. Если указанные характеристики известны, тогда для определения объема усеченной пирамиды следует воспользоваться формулой:

V = 1/3 × h × (So1 + So2 + √ (So1 × So2)).

Например, для четырехугольной правильной фигуры, длины сторон оснований которой равны B и b, приходим к следующему выражению для объема:

V = 1/3 × h × (B2 + b2 + B × b).

Пример решения задачи

Рассмотрев, что такое усеченная пирамида, а также разобравшись с необходимыми для описания ее характеристик формулами, покажем, как их использовать на практике.

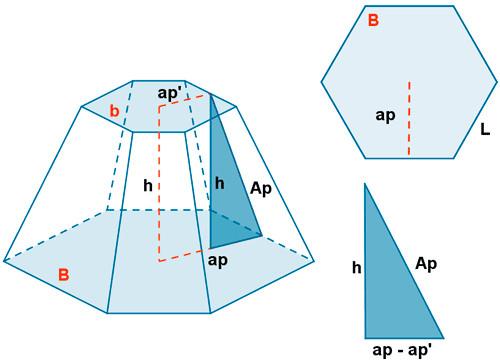
Предположим, что имеется шестиугольная усеченная фигура, которая показана ниже.

Необходимо рассчитать ее объем, если известны стороны оснований B и b и апофема Ap.

Для начала рассчитаем площадь каждого из оснований, которая соответствует площади правильного шестиугольника. Имеем:

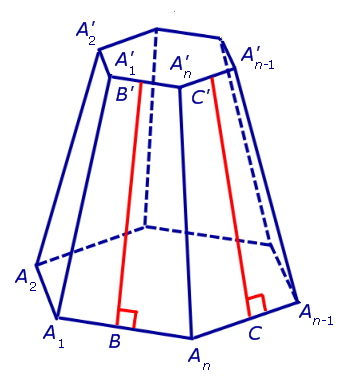
Для определения объема необходимо вычислить через Ap высоту h фигуры. Рассматривая изображенный на рисунке прямоугольный треугольник и применяя теорему Пифагора, получаем:

Тогда объем этой шестиугольной усеченной пирамиды будет равен:

Пирамиды индейцев майя

Если египетские пирамиды с точки зрения геометрии представляют собой правильные полные четырехугольные фигуры, то аналогичные сооружения индейцев майя являются четырехугольными усеченными пирамидами.

Эти памятники культуры, сохранившиеся до наших дней, некогда выполняли двойную роль для своих жителей: с одной стороны, они служили гробницей вождям, с другой же стороны, на их верхнем основании располагался храм, где жрецы поклонялись богам.

Источник

Геометрические фигуры. Усеченная пирамида.

Усеченной пирамидой является многогранник, заключенный меж основанием пирамиды и секущей плоскостью, которая параллельна ее основанию.

Или другими словами: усеченная пирамида — это такой многогранник, который образован пирамидой и ее сечением, параллельным основанию.

Сечение, которое параллельно основанию пирамиды делит пирамиду на 2 части. Часть пирамиды меж ее основанием и сечением — это усеченная пирамида.

Это сечение для усеченной пирамиды оказывается 1-ним из оснований этой пирамиды.

Расстояние меж основаниями усеченной пирамиды является высотой усеченной пирамиды.

Усеченная пирамида будет правильной, когда пирамида, из которой она была получена, тоже была правильной.

Высота трапеции боковой грани правильной усеченной пирамиды является апофемой правильной усеченной пирамиды.

Свойства усеченной пирамиды.

1. Каждая боковая грань правильной усеченной пирамиды является равнобокими трапециями одной величины.

2. Основания усеченной пирамиды являются подобными многоугольниками.

3. Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.

4. Боковые грани усеченной пирамиды являются трапециями.

5. Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.

Формулы для усеченной пирамиды.

Для произвольной пирамиды:

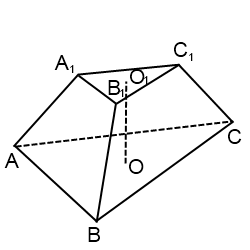
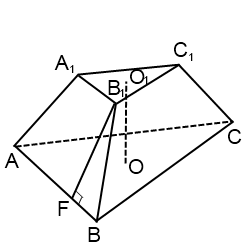
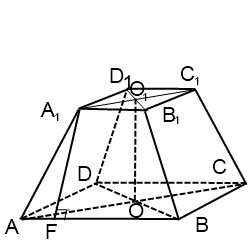
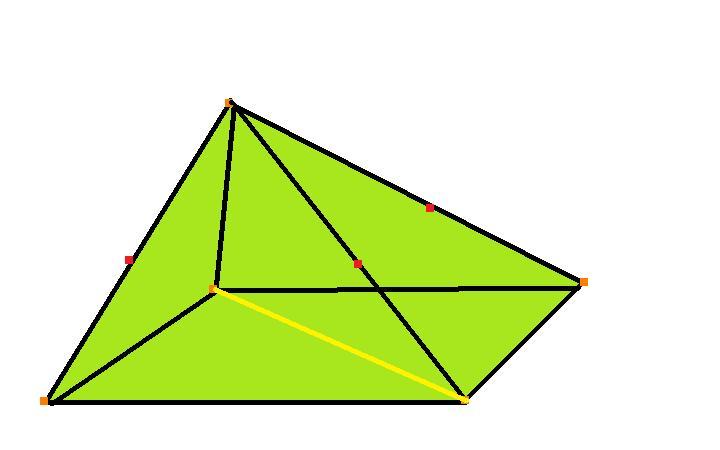
Объем усеченной пирамиды равен 1/3 произведения высоты h (OS) на сумму площадей верхнего основания S₁ (abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

h — высота усеченной пирамиды.

Площадь боковой поверхности равняется сумме площадей боковых граней усеченной пирамиды.

Для правильной усеченной пирамиды:

Правильная усеченная пирамида — многогранник, который образован правильной пирамидой и ее сечением, которое параллельно основанию.

Площадь боковой поверхности правильной усеченной пирамиды равна ½ произведения суммы периметров ее оснований и апофемы.

φ — двугранный угол у основания пирамиды.

CH является высотой усеченной пирамиды, P₁ и P₂ — периметрами оснований, S₁ и S₂ — площадями оснований, S_бок — площадью боковой поверхности, S_полн — площадью полной поверхности:

Сечение пирамиды плоскостью, параллельной основанию.

Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) разделяет высоту и боковые ребра пирамиды на пропорциональные отрезки.

Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) – это многоугольник, который подобен основанию пирамиды, при этом коэффициент подобия этих многоугольников соответствует отношению их расстояний от вершины пирамиды.

Площади сечений, которые параллельны основанию пирамиды, относятся как квадраты их расстояний от вершины пирамиды.

Источник

Усечённая пирамида

Усечё́нная пирами́да — многогранник, образованный пирамидой и её сечением, параллельным основанию.

Содержание

Произвольная усечённая пирамида

Формулы для усечённой пирамиды

Объём пирамиды , где — площади оснований, — высота усечённой пирамиды.

Площадь боковой поверхности равна сумме площадей боковых граней усечённой пирамиды.

Правильная усечённая пирамида

Определение

Правильная усечённая пирамида — многогранник, образованный правильной пирамидой и её сечением, параллельным основанию.

Формулы

См. также

Многогранники
Правильные (Платоновы тела)	Трёхмерные Правильный тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр Четырёхмерные 6 правильных многогранников Большей размерности N-мерный куб • N-мерный октаэдр • N-мерный тетраэдр
Звёздчатый додекаэдр • Звёздчатый икосододекаэдр • Звёздчатый икосаэдр • Звёздчатый многогранник • Звёздчатый октаэдр
Выпуклые	Архимедовы тела Кубооктаэдр • Икосододекаэдр • Усечённый тетраэдр • Усечённый октаэдр • Усечённый икосаэдр • Усечённый куб • Усечённый додекаэдр • Ромбокубоктаэдр • Ромбоикосододекаэдр • Ромбоусечённый кубоктаэдр • Ромбоусечённый икосододекаэдр • Курносый куб • Курносый додекаэдр • Усечённый кубооктаэдр • Усечённый икосододекаэдр • Правильная призма • Антипризма Каталановы тела Ромбододекаэдр • Ромботриаконтаэдр • Триакистетраэдр • Тетракисгексаэдр • Пентакисдодекаэдр • Триакисоктаэдр • Триакисикосаэдр • Дельтоидальный икоситетраэдр • Дельтоидальный гексеконтаэдр •Пентагональный икоситетраэдр • Пентагональный гексеконтаэдр • Дисдакисдодекаэдр • Дисдакистриаконтаэдр Без полной пространственной симметрии Пирамида • Призма • Бипирамида • Антипризма • Зоноэдр • Параллелепипед • Ромбоэдр •Призматоид• Усечённая пирамида• Пентагондодекаэдр • Параллелоэдр
Формулы, теоремы, теории	Полезное Смотреть что такое «Усечённая пирамида» в других словарях: Усечённая пирамида — геометрическое тело (рис.), отсекаемое от пирамиды (См. Пирамида) плоскостью, параллельной основанию. Объём У. п. равен s1 и s2 – площади оснований, h – высота (расстояние между основаниями). К ст. Усечённая пирамида … Большая советская энциклопедия Усечённый икосаэдр — Для увеличения, щёлкните по картинке. Вращение фигуры Тип Полуправильный многогранник Грани … Википедия УСЕЧЁННЫЙ — УСЕЧЁННЫЙ, ая, ое. В математике: такой, у к рого вершинная часть отделена, отсечена плоскостью, параллельной основанию. У. конус. Усечённая пирамида. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова Пирамида (геометрия) — У этого термина существуют и другие значения, см. Пирамидацу (значения). Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обcуждения могут быть пояснения … Википедия ПИРАМИДА — [от греч. pyramis (pyramidos)] многогранник, основание к рого многоугольник, а остальные грани треугольники, имеющие общую вершину (рис. 1). По числу углов основания различают П. треугольные, четырёхугольные и т. д. Объём пирамиды V = 1/2Sh. Если … Большой энциклопедический политехнический словарь УСЕЧЁННЫЙ — УСЕЧЁННЫЙ, усечённая, усечённое; усечён, усечена, усечено. 1. прич. страд. прош. вр. от усечь (книжн.). 2. Такой, у которого верхняя часть отсечена плоскостью, параллельной основанию (о конусе, пирамиде; мат.). Усечённый конус. Усеченная пирамида … Толковый словарь Ушакова Призматоид — ― многогранник, две грани которого (основания призматоида) лежат в параллельных плоскостях, а остальные являются треугольниками или трапециями, причём у треугольников одна сторона, а у трапеций оба основания являются сторонами оснований… … Википедия Бипирамида — или дипирамида является трёхмерным многогранником, сформированным из двух пирамид, одна из которых является зеркальным отражением другой. Место соединения пирамид образует общую фигуру в виде многоугольника. Простая бипирамида формируется при… … Википедия Правильный многогранник — Додекаэдр Правильный многогранник или платоново тело это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией … Википедия Источник Усеченные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности усеченной пирамиды Усеченные пирамиды Расстояние между плоскостями Расстояние между плоскостями оснований усеченной пирамиды называют высотой усеченной пирамиды. Множество всех боковых граней усеченной пирамиды составляет боковую поверхность усеченной пирамиды. Полная поверхность усеченной пирамиды состоит из оснований усеченной пирамиды и ее боковой поверхности. Теорема Эйлера. Для любой усеченной пирамиды справедливо равенство: то теорема Эйлера доказана. Правильные усеченные пирамиды Определение 2. Высоту боковой грани правильной усеченной пирамиды называют апофемой правильной усеченной пирамиды (рис 4). Свойства правильной усеченной пирамиды: Все боковые ребра правильной усеченной пирамиды равны. Все боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями. У любой правильной усеченной пирамиды все апофемы равны. Все боковые ребра правильной усеченной пирамиды образуют с плоскостью нижнего основания усеченной пирамиды равные углы. Все боковые ребра правильной усеченной пирамиды образуют с плоскостью верхнего основания усеченной пирамиды равные углы. Все боковые грани правильной усеченной пирамиды образуют с плоскостью нижнего основания усеченной пирамиды равные двугранные углы. Все боковые грани правильной усеченной пирамиды образуют с плоскостью верхнего основания усеченной пирамиды равные двугранные углы. Отрезок, соединяющий центры верхнего и нижнего оснований правильной усеченной пирамиды, перпендикулярен плоскостям оснований правильной усеченной пирамиды. Длина этого отрезка равна высоте правильной усеченной пирамиды. Источник Узнать ещё Знание — сила. Познавательная информация Усеченная пирамида Плоскость, параллельная основанию пирамиды, разбивает исходную пирамиду на две части: пирамиду, подобную данной, и усеченную пирамиду. Усеченная пирамида ограничена основаниями — двумя параллельными подобными многоугольниками, — и боковой поверхностью. Соответствующие стороны многоугольников в основаниях попарно параллельны, поэтому боковые грани усеченной пирамиды — трапеции. Высота усеченной пирамиды — это расстояние между плоскостями ее оснований. Как построить усеченную пирамиду? Чтобы построить усеченную пирамиду: 1) строят полную пирамиду; 2) проводят сечение, параллельное основанию; 3) верхнюю часть чертежа стирают. Объем усеченной пирамиды Формула объема усеченной пирамиды: где S1 и S2- площади оснований пирамиды, H — высота пирамиды. Правильная усеченная пирамида Усеченная пирамида, полученная из правильной пирамиды, называется правильной усеченной пирамидой. Боковые грани правильной усеченной пирамиды представляют собой равные равнобокие трапеции. Их высоты называют апофемами. Боковая поверхность правильной усеченной пирамиды. Площадь боковой поверхности правильной усеченной пирамиды может быть найдена по одной из формул: где P1 и P2 — периметры оснований, l — апофема. где φ- двугранный угол при большем основании пирамиды. Источник ← олх квартиры усть каменогорск отделка двора частного дома → Вам также понравится Ночной апноэ у детей что это такое 18.10.202322.08.2023 admin 0 сода с уксусом что получится 14.10.202325.08.2023 admin 0 проект щита для квартиры 18.10.202316.08.2023 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email *