Общее свойство множества что это

Основные свойства множеств.

Рассмотрим теперь кратко простые теоретико-множественные понятия и теоретико-множественные операции: пересечение, объединение, дополнение, декартово произведение и др. Для случая конечных множеств они лежат в основе арифметических действий над натуральными числами и поэтому очень важны для школьной математики. Мы ограничимся совсем краткими определениями и пояснениями.

Множество не содержащее ни одного элемента называют пустым множеством. Его обозначается знаком. Пустое множество можно определить любым противоречивым свойством, например= <х | xх>, в области множеств оно играет как бы роль нуля.

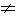
Множество N называется подмножеством множества М тогда и только тогда, когда каждый элемент множества N принадлежит множеству М. Отношение между множеством М и любым его подмножеством N называется включением и обозначается символом: МN.

Отметим следующие элементарные утверждения о понятиях подмножества и включения, прямо вытекающих из определения.

а) Каждое множество М является подмножеством самого себя: ММ. Любое подмножество N множества М, отличное от М, называется собственным подмножеством множества М; соответствующее включение также называется собственным и обозначается: МN. Принято считать, что пустое множествоявляется подмножеством любого множества М.

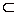
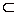
б) Отношение включения транзитивино, т. е. из NМ и РN следует, что РМ. Транзитивно также отношение собственного включения.

в) Очень важно не смешивать отношения принадлежностии включения: если <а>М, то аМ, и наоборот; но из М не следует <а>М. Так, например, если М = <1, 2>, то это означает, что 1М и 2М, но для всех других объектов х справедливо х М; для включения же правильны следующие утверждения:

М, <1>М, <2>М., <1, 2>М.

Другой пример. Пустое множествоне имеет элементов хM для любого объекта х. Между темсодержит одно подмножество, а именно само себя.

Введем несколько операций над множествами.

а) Пересечением множеств М и N называют множество тех объектов, которые принадлежат множествам М и N одновременно.

Обозначение: МN = <х|хМ и хN>.

б) Объединением множеств М и N называют множество тех элементов, которые содержатся по крайней мере в одном из множеств М или N. Обозначение: MN = <х | хМ или х N >.

в) Разностью множеств М и N называют множество тех элементов, которые принадлежат множеству М и не принадлежат множеству N. Обозначение: М \ N. = <х | хМ и хN>.

Обозначение: MN =< x | (xМ и хN) или (хN и хМ)>.

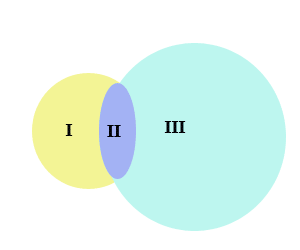
Введенные теоретико-множественные операции наглядно иллюстрируются рисунком 2, где множества М и N изобрансены пересекающимися кругами:

М N — точки области II;

М N — точки областей I, II, III;

М \ N — точки области I;

N \ М — точки области III;

M N — точки областей I и III.

д) В конкретных математических областях бывает полезно ввести в рассмотрение столь обширное множество U, что все рассматриваемые множества окажутся его подмножествами. Такое множество U принято называть универсальным множеством или универсумом. Отметим, что «универсальное множество» понятие относительное: оно выбирается для какого-нибудь определенного раздела науки и притом часто даже явно не определяется, а просто подразумевается.

Так, например, в элементарной планиметрии в качестве универсального множества принято рассматривать множество всех точек плоскости. Различные фигуры, изучаемые в планиметрии, можно считать множествами точек, т. е. подмножествами так выбранного универсального множества.

В элементарной арифметике универсальным множеством считается множество Z всех целых рациональных чисел и т. д.

М = <х | хU и xM>

Таким образом, дополнение — это частный случай разности:

M = U \ M,
все отличие здесь состоит в том, что разность берется относительно фиксированного множества, содержащего все множества, которые в данной связи рассматриваются.

Самостоятельный интерес представляет тот частный случай, когда множества А и В совпадают: А = В. Чтобы его рассмотреть, вы введем новый термин.

Упорядоченной парой элементов множества А будем называть объект (а₁, а₂), состоящий из двух (не обязательно различных) элементов а₁, а₂А, с указанием, какой из них следует считать первым, а какой — вторым. Так, например, если А = <1, 2, 3, 4., 5>, то упорядоченные пары (2, 3) и (3, 2) следует считать по определению различными. Упорядоченными парами элементов из А считаются также объекты (1, 1), (2, 2), (3, 3), (4, 4), (5, 5). Упорядоченные пары мы будем заключать в круглые скобки и обозначать жирными строчными латинскими буквами: a = (а₁ а₂), в отличие от неупорядоченных пар, которые, как и множества элементов, записываются в фигурных скобках: <а₁ а₂>.

Рассмотренные свойства множеств и операции над ними в неявном, виде присутствуют в начальном преподавании арифметики. Мы особенно подчеркиваем, что речь идет об их неявном присутствии: бессмысленно было бы в I или II классе давать явные определения арифметических действий. Само слово «действие» для арифметических операций указывает на то, что на начальном уровне развития детей сложение, вычитание, умножение и деление возникают как действия над конкретными множествами из мира, свойственного школьникам. Вековой опыт обучения на всех уровнях показывает, что человек обычно сначала делает нечто, а лишь затем задумывается над тем, какими же общими свойствами обладают его действия.

Теоретико-множественное обоснование арифметических действий над натуральными числами дается довольно элементарно, так как более строгое обоснование оказывается достаточно трудоемким и мы не имеем возможности провести его здесь со всей необходимой тщательностью. Как мы уже говорили, с точки зрения теории множеств натуральные кардинальные числа отвечают классам равнамощных конечных множеств, к ним, естественно, присоединяется и число нуль как кардинальное число, соответствующее пустому множеству. Тогда элементарные отношения и действия над натуральными числами вводятся следующим образом.

1.Отношение «равно», «больше», «меньше». Пусть m и n — два натуральных числа и пусть М и N — два множества, кардинальные числа которых суть соответственно m и n. Тогда m меньше n (а n больше m), если множество М равномощно некоторому собственному подмножеству множества N. Как видно из этого же определения, m = n означает, что множества М и N равномощны. Для оправдания такого определения необходимо, конечно, показать, что оно не зависит от выбранных множеств М и N. Иначе говоря, надо доказать, что если М’ и N’ — два других множества с числом элементов m и n соответственно и если при этом М равномощно собственному подмножеству множества N’, то и М’ равномощно собственному подмножеству множества N’, и наоборот. Это доказательство мы предоставим читателю. Отметим, что определение неравенства для бесконечных кардинальных чисел получается более сложным.

2.Сложение. Для определения суммы кардинальных чисел поступают так. Пусть m и n — два натуральных числа. Выбираем опять произвольно два непересекающихся множества М с m N с n элементами соответственно, и пусть S — их объединение: S = MN. Тогда по определению сумма s = m + n — это кардинальное число множества S. Покажем, что сумма s от выбора множеств M и N не зависит, а зависит только от их мощностей. Пусть М’ и N’— другие множества, равномощные множествам М и N соответственно, и пусть при этом также M’N’ =; тогда S’ = М’N’ равномощно множеству S = МN. Следует все время иметь в виду, что кардинальное число объединения есть сумма кардинальных чисел объединяемых множеств, только если последние не имеют общих элементов (имеют пустое пересечение). В случае пересекающихся множеств имеет место более общее, правило:

|M x N| = |M||N|

Источник

Что такое множество 👨‍🎓. Свойства и операции над множествами

В этой статье рассмотрим очень важную тему, как в математике, так и в информатике – множества. Ниже Вы найдете основные определения и понятия, свойства множеств, их виды и примеры. Материал изложен таким образом, что разберется даже полный чайник. Здесь приведены, только основы, которые обычно проходятся в рамках школьной программы. Читайте!

Основные положения и обозначения

Теория множеств появилась благодаря знаменитому немецкому математику Гео́рг Ка́нтор (3 марта 1845, Санкт-Петербург — 6 января 1918, Галле (Заале)) — немецкий математик, ученик Вейерштрасса. Наиболее известен как создатель теории множеств.

Итак, начнем с основных понятий. Основное определение имеет следующий вид:

Множества (м-ва – сокр.) – наборы элементов объединенных по какому либо признаку.

Обозначаются они с помощью заглавных латинских букв, а их элементы указываются в фигурных скобках.

Примеры

​ \( S = \left\ < а, б, в, г, д, …, ю, я \right\>\) – мн-во букв русского алфавита.
\( S = \left\ < Алексей, Анатолий, Галина, …, Александр, Ирина \right\>\) – мн-во имен студентов в группе.
\( S = \left\ < 🐵, 🙈, 🙉, 🙊 \right\>\) – мн-во смайликов с изображением обезьянок.

Также стоит обговорить про принадлежность элементов к множеству. Записать её можно с помощью специального значка «принадлежности» – ​ \( \in \) ​. Так запись вида \( x \in S \) обозначает, что элемент x принадлежит множеству S.

С основным понятием разобрались, перейдем к остальной теории.

Подмножества

Подмножество – множество S1 является подмножеством S, если каждый элемент из S1 содержится (включен) в S.

Обозначают подмножества при помощи специального значка «включения», который имеет вид ​ \( \subset \) \( (\ S_1 \subset S \ ) \) ​. Также их можно отобразить схематично, используя диаграммы Эйлера, которые отображают отношения между подмножествами.

Также Вы можете выделить подмножество мужских имен, или сделать любую выборку по какому-нибудь признаку.

Мощность

Следует также выделить такое понятие, как мощность. Имеет оно следующий вид:

Мощность – количество элементов, которое содержится в множестве.

Мн-ва называются равномощными тогда и только тогда, когда количество элементов одного из них равно количеству элементов другого.

Причем неважно, какие элементы будут в этих мн-ах. Так в одном из них могут содержаться 26 букв английского алфавита, а в другом 26 марок японских автомобилей, при этом они будут равномощными.

Мощность является одним из тех свойств, благодаря которому мы можем проводить сравнение двух (или более) м-в.​​

Равенство

Необходимо сказать и про равенство. Для чайников правило будет выглядеть так:

Два (или несколько) множеств равны только тогда, когда равны все их элементы.

Теперь изучим виды и другие свойства мн-в в математике.

Существует много критериев и свойств, по которым мы можем классифицировать множества. Например, мы можем разделить их по количеству элементов:

А можем поделить их на конечные (ограниченные) и бесконечные:

Теперь рассмотрим примеры множеств в математике.

Примеры

Натуральные числа

Натуральные числа в математике – это те числа, которые мы используем при счете (1, 2, 3 и т.д.). Сюда не относятся отрицательные величины и нуль. Запись: \( N = \left\ < 1, 2, 3, 4, 5, … \right\>\).

Целые числа

Получаются из множества натуральных чисел. К ним добавляются отрицательные числа и нуль. \( Z = \left\ < 0, \pm 1, \pm 2, \pm 3, \pm 4, \pm 5, … \right\>\).

Рациональные числа

Здесь множество задается следующим образом: ​ \( Q = \left\ < \ | \ m \in Z, \ n \in N\right\> \) ​. В формуле m представляет собой целый числитель, а n – натуральный знаменатель.

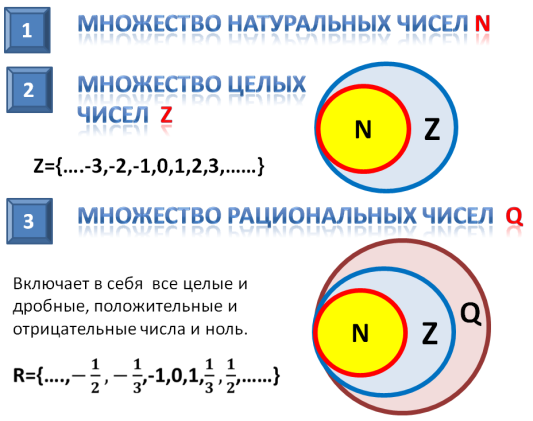
Так как любое число в математике можно представить в виде дроби (например, ​ \( 5 = <5 \over 1>\) ​), то целые числа являются подмножеством рациональных чисел. Натуральные же числа являются подмножеством целых чисел.

\[ N \subset Z \subset Q \]

Эту теорию Вам надо запомнить.

Операции

В этом разделе рассмотрим основные операции (действия) над множествами в математике.

Пересечение

Чтобы поняли даже чайники, вернемся к нашим «мартышкам»:

\( S_ <1>= \left\ < 🙉, 🙊 \right\>\) — обезьянки показывающие лапки и глаза

\( S_ <2>= \left\ < 🙈, 🙉 \right\>\) — мартышки показывающие лапы и рот

Надо найти \( S_ <1>\ \cap \ S_ <2>\). Для этого воспользуемся диаграммами Эйлера — Венна:

Решение: ​ \( S_ <1>\ \cap \ S_ <2>= \left\ < 🙉 \right\>\) т.к. 🙉 ​ входит и в S1 и в S2.​

Объединение

​Решение: ​ \( S_ <1>\ \cup \ S_ <2>= \left\ < 🙈, 🙉, 🙊 \right\>\) ​

Разность

Решение: ​ \( S_ <1>\ \setminus \ S_ <2>= \left\ < 🙊 \right\>\)

Следует отметить, что здесь приведены не все операции. Например, не написано про симметрическую разность и законы Моргана. Их проходят в рамках высшей математики.

Заключение

Теперь Вы знаете, что такое мн-ва, знаете их свойства и какие операции над ними можно выполнять. Надеюсь я объяснил всю теорию так, что понял даже полный чайник. Если же у Вас возникли вопросы, то задавайте их в комментариях. Также на нашем сайте Вы можете прочитать другие статьи, например про представления чисел в компьютере. Рассказывается как выполнять с ними такие действия, как перемножение, получение суммы и деление.

Источник

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками < >.

А = <а, в, с, у>– А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = , а Є N – элемент «а» принадлежит N.

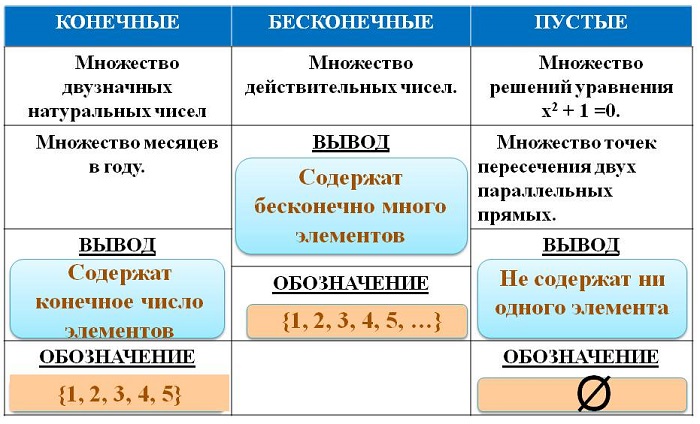
Выделяют три вида множеств:

пустые (обозначаются Ø) – не имеющие элементов.

Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

Множество натуральных чисел

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

Следовательно, N и Z являются подмножествами Q.

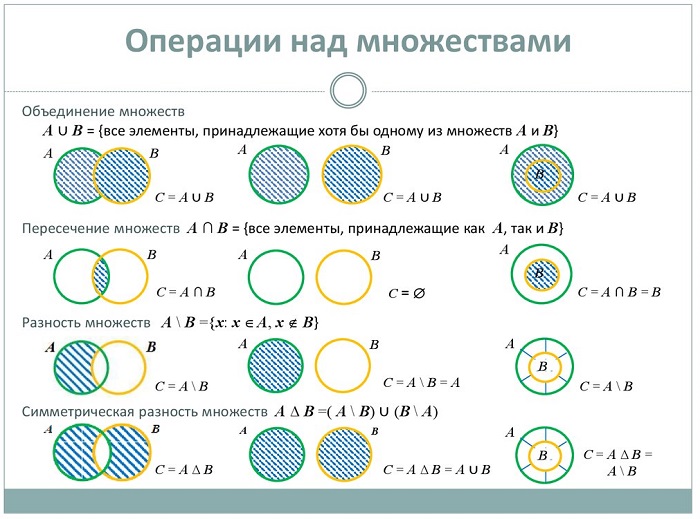
Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;

сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);

сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);

умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);

сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

если S ⊆ Fи F ⊆ J, то S ⊆ J;

если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

О других свойствах операций можно узнать из картинки:

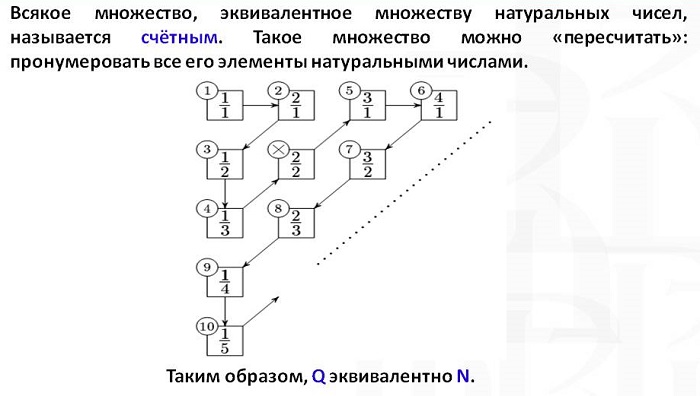
Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Источник