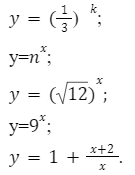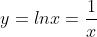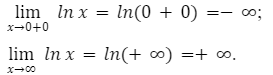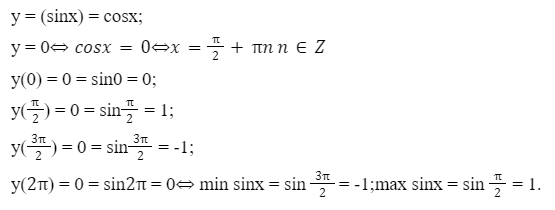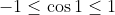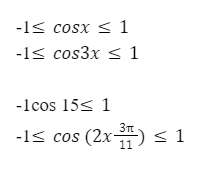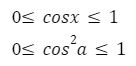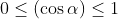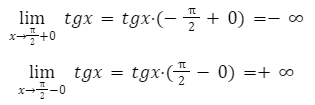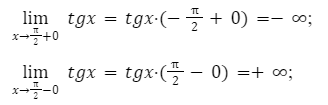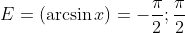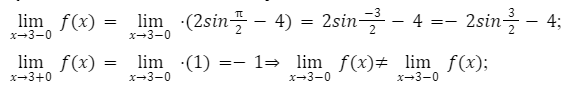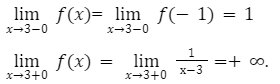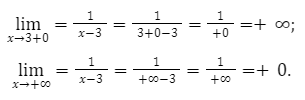Область значения функции что это
Область значений функции
Время чтения: 40 минут
Область значений функции, ее свойства и примеры решения
В данном материалы мы подробно рассмотрим значение функции. Определим основные методы ее вычисления. Изучим множество значений функции.
Подробно, разберем на примерах, методы нахождения функции. Прежде, чем начать изучение материала, охарактеризуем основное определение значению функции.
Функции удобно изображать в виде графических прямых или кривых.
Понятие области определения функции
Функция задается тогда, когда любому значению, например x соответствует любое значение y. Независимой переменной называют значение х или по другому аргументом. Числовое значение y, как правило является зависимой переменной.
Данная зависимость между x и y в алгебре называют функциональной. Записывают ее в виде функции y = f(x)
Другими словами, функция, это когда значения одной переменной зависят от значений другой переменной.
Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.
Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.
Например:
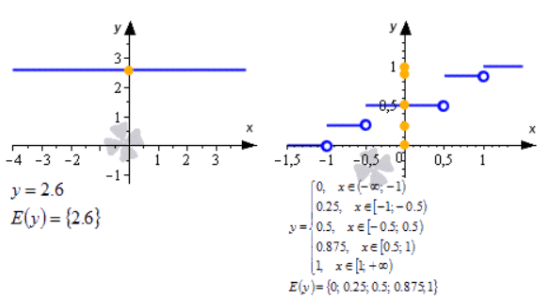
Область значений функции y = z 2 — это все значения, которые будут больше либо равные нулю. В виде записи это выглядит следующим образом: f(у): у ≥ 0. Не все функции обозначаются одинаковыми формулировками, в основном D(f). Но тригонометрические функции обозначаются немного иначе. D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус. Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = x. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1]. Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Для указания множества чисел в определенном промежутке, необходимо выполнить следующие действия:
Если у промежутка нет правой границы, записываем знак бесконечности или плюс бесконечности. Если отсутствует левая граница, записываем знак минус бесконечности.
В случае, если записывается множество, которое состоит из нескольких промежутков, ставится знак объединение.
Рассмотрим на примерах
Все действительные числа от 1 до 9, можно выразить в следующей записи. [1;9]
Все положительные числовые значения, имеют следующий вид: (0; +);
Так как ноль, не является положительным число, то возле него ставится круглая скобка.
Область значения и определения функции
Чаще всего область определения выражают как функцию D(y).
В математике существует две главных запрещенных (недопустимых) операции:
При определении области функции, вступают в силу два основных ограничения:
Область определения постоянной функции
Постоянная функция записывается обычной формулой y = N, а именно f(x) = N, где N — любое действительное число. Иными словами, принято называть константа.
Постоянная функция — это функция, при которой всегда наблюдается одно и то же числовое значение, независимо от того какое числовое значения имеет аргумент.
Область определения степенной функции
Область определения степенной функции, всегда имеет непосредственную зависимость, от значений показателя степени.
Рассмотрим основные моменты:
Если k — неотрицательное целое число, то областью определения данной функции является множество любых, обязательно, действительных чисел: (-∞, +∞).
Когда степенной показатель, является не целое число, то функция имеет следующий вид D(f) = [0, +∞).
Когда k — отрицательное целое число, то область определения функции представляет собой (-∞, 0) ∪ (0, +∞).
Для остальных действительных отрицательных, a область определения степенной функции — числовой промежуток (0, +∞).
Если k равно нулю, то функция определена для всех чисел, кроме нуля. Так как ноль нельзя возвести в степень, а любое другое число в нулевой степени равно 1.
То есть, при k = 0, y =x0 = 1, на заданной области определения (-∞, 0) ∪ (0, +∞).
Область определения показательной функции
Показательная функция записывается как: y=k x
где значение x — показатель степени;
k — число, которое обязательно больше нуля и не равно единице.
Область определения показательной функции — это множество значений R.
Основные примеры показательных функций:
Область определения, для этих функций, записывается следующим образом: (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выражается как: y=log n k
Рассмотрим на примере, характер решения задачи данной функции.
Пример №1
y=ln x, определить область определения натурального логарифма. D(y)=(0;+).
На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.
Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.
Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.
Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.
Ответ: множество всех действительных чисел, это и есть область значений функции ln.
Область определения и множество значений функций косинус, синус, тангенс, котангенс
Множество значений всех действительных чисел, будет являться областью определения функций синус и косинус, и записываться следующим образом.
Функции являются ограниченными, как сверху, так и снизу.
y = sin x и y = cos x
Промежуток их действия сводится к неравенству -1 ≤ y ≤ 1
Областью определения функции тангенс tg x, является выражение 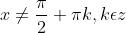
Областью определения функции y = сtg x является множество чисел 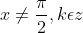
На нижеприведенных примерах подробно расписано решение задач, при определении области функции, при заданных промежутках значений.
Пример №1
Определить область значения функции sin x
Данный вид функции относится к категории периодической. Ее период равняется 2π
Определяем множество значений на следующем отрезке: (0;2π).
Пример №2
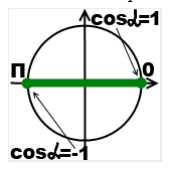
Необходимо определить область значения функции cos x.
Наименьшее значение равно -1;
Минимальное значение косинуса равняется -1, потому что наименьшее значение х, на окружности стремится к этому значению и, следовательно, равняется -1.
Максимальное значение косинуса будет соответственно 1. Поскольку значение на окружности х имеет число 1.
Область значение, следовательно, будет от минус одно до плюс одного. [-1;1].
Применяем двойное неравенство и записывает следующее выражение:
Область значения косинуса никогда не зависит от аргумента, только если сам аргумент выражен в виде сложного выражения. Где имеют место ограничения касающиеся области определения и области значения.
Таким образом, минимальное значение cos x, cos (15α), cos(5-11x) и так далее, будет однозначно равняться -1;
Самым максимальным значением cos x, cos(4φ), cos(5х+3) равняется 1.
Область значений функции y=cos x — также промежуток [-1;1].
Область значения квадрата косинуса, будет промежуток от нуля до единицы [0;1]. Потому что число в четной степени, является не отрицательным.
Аналогичным образом находим область значений модуля косинуса — промежуток [0;1]
Пример №3
y = tgx на определенном интервале 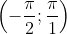
Решение:
Из правил алгебры, известно, что производная тангенса имеет положительное значение. Соответственно функция будет иметь возрастающую характеристику.
Далее необходимо определить поведение функции, в заданных пределах.
Выполнив решение, мы получаем рост значений от минус до плюс бесконечности. Решение будет сводится к следующему: множество решение заданной функции, будет множество всех действий функции.
Пример №4
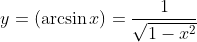
Решение:
Для всех значений x производная будет положительной, в пределах от -1;1
Следовательно, область значения арксинуса равняется:
Пример №5
Разберем функцию 2sinx2-4, где значение х меньше либо равно значению 3. Необходимо вычислить область значений.
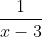
Функция является для всех значений x определенной.
Наблюдаем недопустимый вид при значении аргумента − 3.
При приближении к данному аргументу функция стремится к 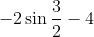
Наблюдается разрыв в точке 3. Когда функция стремится к данному разрыву ее числовые значения приближаются к -1. Минус бесконечность будет наблюдаться при стремлении к такой точке, но только с правой стороны.
Из этого следует вся область значений данной функции разбивается на три интервала. (-;−3], (−3 ;3], (3;+)(-;-3], (-3; 3], (3;+).
Первый интервал имеет функцию, следующего вида 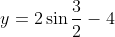
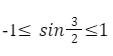
На промежутке -∞;-3, функция имеет следующие значения [-6;-2].
Функция y=-1, получается на полуинтервале (−3;3]. Следовательно, все значения будут сводится на данном интервале к одному числу, а именно -1.
Проанализируем второй промежуток (3;-+∞). Так как функция 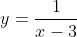

Если значение x больше значения 3, то большинство множеств функции будет в промежутке от нуля до +∞.
Определение числовой функции. Область определения функции. Область значения функции.
Что такое область определения функции? что такое область значения функции? Давайте, в этой статье разберемся в понятиях числовой функции и ее характеристиках и свойствах.
Определение функции.
Функция y=f(x) — это когда каждому допустимому значению переменной x соответствует единственное значение переменной y или другими словами такая зависимость переменной y от переменной x.
х — называется независимой переменной или аргументом.
y – называется зависимой переменной или значением функции.
Множество чисел, где x∈X или D(f) — называется областью определения функции. Это множество всех допустимых значений переменной х.
Область значений функций, когда задаем правило или функцию, которая позволяет по произвольно выбранному значению x∈D(f) вычислить соответствующее значение y.
Переменную х или аргумент мы придумываем сами и подставляем в правило, которое задали или функцию. Далее рассчитываем переменную y или значение функции.
В тех диапазонах в которых существует переменная х называется областью определения функции.
В тех диапазонах в которых существует переменная y называется областью значения функции.
Графиком функции y=f(x), x∈X называется множество точек (x; f(x)) координатной плоскости.
Разберём пример №1:
Найдите область определения и область значения числовой функции y=x 2
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.
А теперь рассмотрим переменную у. В таблице мы видим, что переменная y принимает положительные значение, так как и самое минимальное значение 0. Следовательно, y∈[0; +∞).
Если посмотрим на график, то увидим, что графика ниже нуля нет. Следовательно, область значения функции E(f) = [0; +∞).
Разберём пример №2:
Найдите область определения и область значения числовой функции y=x+1?
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.

Рассмотрим переменную у. В таблице мы видим, что переменная y также принимает значения как в положительном, так и в отрицательном направлении. Следовательно, ограничений у переменной y нет, y∈(−∞; +∞). Область значения функции E(f) = (−∞; +∞).
Область значения функции
Что такое функция в алгебре
Функция в алгебре — некое математическое выражение y=f(x), где каждому значению переменной x соответствует одно значение переменной y.
Из этого следует, что решений у функции может быть много. Для обозначения совокупностей таких решений вводятся особые термины.
Множество значений функции y=f(x) — совокупность значений переменной y, которые она принимает при переборе всех значений переменной x на заданном отрезке X.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Областью значений функции y=f(x) называется такое множество значений, которые функция y принимает при переборе всех значений аргумента x из области определения. Область значений обозначается как E(f).
Область допустимых значений (область определения) функции — такое множество всех значений переменных, при которых функция имеет смысл, то есть решается.
Область значений функции вместе с областью ее определения формирует границы для отображения данной функции в виде графика.
Виды функций
Для каждой функции, в зависимости от ее структуры, область значений будет своя. Рассмотрим основные виды элементарных математических функций.
Линейная
Область значений включает в себя все действительные числа: \(E(f)=(-\infty;\;+\infty).\)
Обратная пропорциональность
Квадратичная (квадратная)
Координата вершины \(y_0\) рассчитывается так:
Область значений зависит от коэффициента a:
Квадратную функцияю y=x^2 можно рассматривать как частный случай квадратичной или степенной функций. Так как при возведении числа в четную степень результат будет всегда положительным, область значений для нее следующая:
\(\mathrm E(\mathrm f)=\lbrack0;\;+\infty) \)
Степенная
Область значений степенной функции зависит от того, к какому числовому множеству относится показатель степени n:
Показательная
\(\mathrm E(\mathrm f)=(0;\;+\infty) \)
Логарифмическая
\(\mathrm y=\log_<\mathrm a>\left(\mathrm x\right)\)
По своим свойствам логарифмическая функция обратна показательной. Для данных функций область определения и область значений меняются местами соответственно. ОЗ логарифмической функции включает в себя все действительные числа:
\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)
Тригонометрические
Рассмотрим четыре базовые тригонометрические функции:
Область значения тангенса и котангенса включает в себя все действительные числа:
\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)
Типы функций
При определении области значений функции необходимо учитывать ее фундаментальные особенности. Обозначенная выше классификация — не единственная. У математических функций есть некоторые параметры, которые влияют как на саму область значений, так и на выбор методики ее нахождения.
Важные свойства
К наиболее важным для поиска области значений функции относят следующие ее свойства:
Методы нахождения
Поиск области значений функции несколько сложнее, чем определение ОДЗ. В зависимости от вида и типа функции, а также условий задачи для этого могут применяться различные методы.
Перебор значений
Графический метод
Как ясно из названия способа, для его реализации необходимо построить график исследуемой функции. По внешнему виду кривой уже можно делать некоторые выводы. Если линия графика соответствует одному из видов элементарных функций, например, является параболой, то в качестве области значений берется промежуток, соответствующий данному графику.
Если по условию задачи необходимо найти область значений функции на определенном промежутке значений переменной x, то на графике максимальные и минимальные точки становятся очевидными. Это могут быть как общие точки экстремума, так и локальные максимальные и минимальные значения.
Учет непрерывности и монотонности
Данный метод вытекает из предыдущего и позволяет делать некоторые прогнозы об области значений функции исходя из ее свойств. Если на графике видно, что функция не прерывается и монотонно убывает или возрастает на определенном промежутке, можно предположить, что эта тенденция сохранится и дальше.
Например, график квадратичной функции f(x)=x^2 имеет вид параболы с точкой перегиба с координатами (0, 0). Кривая непрерывна, то есть не имеет разрывов в области определения. Для того, чтобы определить область значений данной функции, достаточно построить ее график на ограниченном промежутке. Для примера возьмем \(x\in\lbrack-4;\;4\rbrack\) :
Рисунок 1. Значение непрерывности и монотонности функции для области определения
\(\mathrm E(\mathrm f)=\lbrack0;\;+\infty)\)
Производная, min и max
Описанные выше способы подходят не для всех ситуаций. В общем случае, задача по определению области значений функции всегда сводится к нахождению ее минимального и максимального значения или точек экстремума.
Согласно теореме Ферма, в точках локального экстремума производная исследуемой функции равняется нулю.
Важно понимать, что сами локальный экстремум не обязательно является максимумом или минимумом для функции в целом. Такие точки называются критическими или стационарными. Поэтому, кроме самих точек необходимо определять промежутки возрастания и убывания:
Кроме того, экстремумы функции можно определять по второй производной. Предположим, при исследовании функции обнаружилась некая критическая точка x_1. Для нее справедливы следующие неравенства:
Пример решения
Задача
Так как функция не относится к элементарным и по условию задачи область поиска не ограничена, воспользуемся методом нахождения точек минимума и максимума.
Найдем производную данной функции y’, воспользовавшись формулами из таблицы производных:
Согласно теореме Ферма, в точках экстремума производная равняется нулю.
Начнем решать полученное уравнение:
Так как уравнение равняется нулю, если хотя бы один из множителей равен нулю, разобьем его на три составляющие:
Получим следующие результаты:
Данные точки являются критическими. В итоге мы имеем четыре промежутка:
Чтобы понять, какие из точек являются минимальными и максимальными, необходимо взять по числу из каждого промежутка и решить производную \(y’=4\cdot x^3-4\cdot x \) относительно них. Сам результат вычислений не важен, учитывать нужно только знак: (+) или (-).
На первом и третьем промежутках производная принимает отрицательное значение, на втором и четвертом — положительное. Следовательно, найденные ранее точки \(x_1=-1\;и\;x_3=1\) являются точками минимума, а точка \(x_2=1\) — точкой максимума. Это еще не окончательный результат, так как необходимо понять, на каких промежутках функция возрастает, а на каких — убывает.
Область определения функции \(y=x^4-2\cdot x^2-5\) следующая: