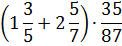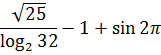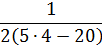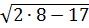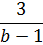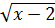О каких выражениях говорят что они не имеют смысла
Выражение, не имеющее смысла: примеры в математике
Выражение – это самый широкий математический термин. По существу, в этой науке из них состоит все, и все операции проводятся тоже над ними. Другой вопрос, что в зависимости от конкретного вида применяются совершенно разнообразные методы и приемы. Так, работа с тригонометрией, дробями или логарифмами – это три различных действия. Выражение, не имеющее смысла, может относится к одному из двух видов: числовому или алгебраическому. А вот что означает это понятие, как выглядит его пример и прочие моменты будут рассмотрены далее.
Числовые выражения
Если выражение состоит из чисел, скобок, плюсов-минусов и остальных знаков арифметических действий, его смело можно называть числовым. Что довольно логично: стоит только еще разок взглянуть на первый названный его компонент.
Числовым выражением может быть что угодно: главное, чтобы в нем не было букв. А под «чем угодно» в данном случае понимается все: от простой, стоящей одиноко, самой по себе, цифры, до огромного их перечня и знаков арифметических действий, требующих последующего вычисления конечного результата. Дробь – это тоже числовое выражение, если в ней нет всяких a, b, c, d и т.д., ведь тогда это совершенно другой вид, о котором будет рассказано чуть позже.
Условия для выражения, которое не имеет смысла
Когда задание начинается со слова «вычислить», можно говорить о преобразовании. Штука в том, что это действие не всегда целесообразно: в нем не то чтобы сильно нуждаются, если на передний план выходит выражение, не имеющее смысла. Примеры бесконечно удивительны: иногда, чтобы понять, что оно-то нас и настигло, приходится долго и нудно раскрывать скобки и считать-считать-считать.
Главное, что нужно запомнить: не имеет смысла то выражения, чей конечный результат сводится к запретному в математике действию. Если уж совсем по-честному, то тогда бессмысленным становится само преобразование, но для того, чтобы это выяснить, приходится его для начала выполнить. Такой вот парадокс!
Самое знаменитое, но от того не менее важное запретное математическое действие – это деление на ноль.
Потому вот, например, выражение, не имеющее смысла:
Если при помощи нехитрых вычислений свести вторую скобку к одной цифре, то она и будет нулем.
По такому же принципу «почетное звание» дается и этому выражению:
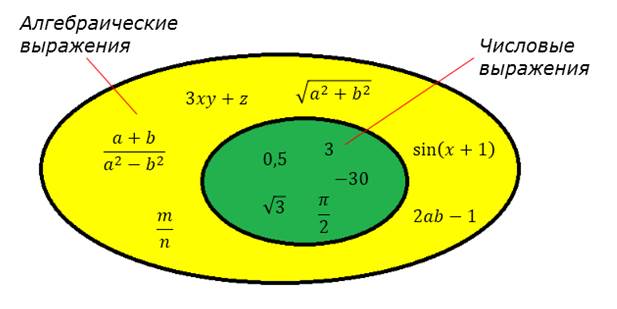
Алгебраические выражения
Это то же самое числовое выражение, если в него добавить запретные буквы. Тогда оно и становится полноценным алгебраическим. Оно также может быть всех размеров и форм. Алгебраическое выражение – понятие более широкое, включающее в себя предыдущее. Но был смысл начинать разговор не с него, а с числового, чтобы было понятнее и разобраться было легче. Ведь имеет ли смысл выражение алгебраическое – вопрос не то чтобы очень сложный, но имеющий больше уточнений.
Почему так?
Буквенное выражение, или выражение с переменными – это синонимы. Первый термин объяснить просто: ведь оно, в конце концов, содержит в себе буквы! Второй тоже не загадка века: вместо букв можно подставлять разные числа, вследствие чего значение выражения будет меняться. Нетрудно догадаться, что буквы в данном случае и есть переменные. По аналогии, числа – это постоянные.
И тут мы возвращаемся к основной тематике: что такое выражение, не имеющее смысла?
Примеры алгебраических выражений, не имеющих смысла
А вот насчет (a+3):(12-4-8) можно смело сказать, что это выражение, не имеющее смысла при любых a.
Типовые задачи по теме «Выражение, не имеющее смысла»
7 класс изучает эту тему по математике в числе прочих, и задания по ней встречаются нередко как непосредственно после соответствующего занятия, так и в качестве вопроса «с подвохом» на модулях и экзаменах.
Вот почему стоит рассмотреть типовые задачи и методы их решения.
Имеет ли смысл выражение:
Необходимо произвести все вычисление в скобках и привести выражение к виду:
Конечный результат содержит деление на ноль, следовательно, выражение не имеет смысла.
Какие выражения не имеют смысла?
Следует вычислить конечное значение для каждого из выражений.
Найти область допустимых значений для следующих выражений:
То есть задание звучит как: найти значения, при которых не будет деления на ноль.
Но на самом деле оно только выглядит страшным и громоздким, потому что на деле содержит в себе то, что уже давно известно: возведение чисел в квадрат и куб, некоторые арифметические действия, такие как деление, умножение, вычитание и сложения. Для удобства, между прочим, можно привести задачу к дробному виду.
Записываем ответ: 3 и 5.
В заключение
Как видно, эта тема очень интересная и не особо сложная. Разобраться в ней не составит труда. Но все-таки отработать пару примеров никогда не помешает!
Про какие числовые выражения говорят что они не имеют смысла?
про какие числовые выражения говорят что они не имеют смысла
Когда с таким числовым выражением делать ничего не надо, т.к. оно не имеет смысла, но что такое числовое выражение? В самом название говорится, что это выражение с числами. Числовое выражение составляется из чисел, знаков математического действия и скобок.
Где, если посчитать то во вторых скобках получается ноль, а на ноль делить нельзя. Это и есть числовое выражение которое не имеет смысла.
А что может не иметь числового значения? То, что мы пытаемся получить при делении на ноль.
Каждый школьник знает, что на ноль делить нельзя, ибо в таком примере не будет решения.
Ниже пример простенькой дроби, которая, как выяснилось, не имеет смысла (так как в знаменателе получается ноль):
Спать мертвым сном совсем не значит уснуть навеки. Это выражение используют тогда, когда хотят сказать, что человек спит так крепко, что его не тревожат посторонние звуки, шум, музыка, громкие разговоры, он спит и не замечает ничего, что происходит вокруг.
Как правило мертвым сном спят только очень уставшие люди, и про них еще говорят, что их не добудишься.
Конечно иметь крепкий сон это хорошо, но мертвый сон говорит о том, что человек исчерпал пределы своих сил.
Счастливая тоска соотносима только с любовью, когда человек тоскует о том, что дорого ему, о встрече с милой, об исполнении заветного желания, которое долго не исполняется. Прдеставьте, ребенок, находящийся долгое время в лагере или на море во сне увидел маму, он просыпается с улыбкой на лице в состоянии счастливой тоски, ему хочется побыстрее увидеть маму.Но счастливая тоска может быть и грустной, если человек знает, что он мечтает о том, что никогда не исполнится.Он увидел во сне маму, он рад этому, но дело в том, что мамы уже давно нет на свете, но всё равно, счастливо тоскуя об ушедшей или ушедшему, человек вспоминает всё лучшее, всё доброе, что было в его жизни связано с мамой. И это великолепно.
13 фраз, которые не запрещены, но очень портят русский язык
Получайте на почту один раз в сутки одну самую читаемую статью. Присоединяйтесь к нам в Facebook и ВКонтакте.
В языке среднестатистического современного человека достаточно много слов, которые не запрещены лингвистами, но раздражают слух. И чаще всего эти слова оказываются действительно неграмотными, а человек, который их употребляет, произнося их тоже выглядит таким. Итак, разбираемся с ошибками в устной речи.
Ещё один распространённый штамп, поработивший наш язык, пришёл из документов. Но только теперь его можно встретить чуть ли не в каждой статье, даже в переписках. «В данном случае» можно заменить на «в этом случае», а «в данном тексте допущена ошибка» написать «в этом тексте допущена ошибка». А лучше вообще обойтись без указательных слов: без них письменная речь выглядит чище.
Слово «касаемо» в русском языке есть, и его употребление не запрещено. Но эта форма считается устаревшей и просторечной. Вместо «касаемо» употребляем оборот «что касается» или «касательно».
«В настоящее время абонент не доступен» — первое, что приходит на ум. От этого выражения, если вы не автоответчик, лучше отказаться. Это слово вполне можно заменить наречием «сейчас», да и канцеляризмы никогда не украшали устную речь и тексты.
Слово «крайний» традиционно использовали в лексиконе люди, чья профессия была связана с риском для жизни. Космонавты, лётчики, альпинисты и подводники нарочито избегают слова «последний», опасаясь, чтобы «последний раз» действительно не стал последним. Их можно понять. Но в какой-то момент слово «крайний» стали употреблять все, кому не лень. Вот такая странная филологическая тенденция.
Итак, как же скучать правильно? В справочнике Розенталя можно встретить замечание о том, что с существительными и местоимениями третьего лица верно говорить: скучать по кому/чему. А вот в первом и втором лице будет «скучать по ком»: по нас, по вас. А вот «скучать за кем-то» или «скучать за чем-то» нельзя – такого словосочетания в русском языке нет.
В русском языке действительно есть глагол «порешать», но употребляться он может только в значении «решать в течение какого-то времени». Например, порешать задачу и бросить. Но сегодня всё чаше выражение «давай порешаем этот вопрос» используют в значении «решить вопрос». Так говорить неправильно. Это жаргонизм, как и «расскажи мне за него» в значении «расскажи мне о нём». В культурном обществе такие фразы употреблять не принято.
Ещё одна распространённая речевая ошибка – «оплатить за проезд». За проезд можно платить, а вот оплачивать только проезд – предлоги здесь недопустимы, поскольку по правилу при переходном глаголе предлог не нужен.
Понравилась статья? Тогда поддержи нас, жми:
Выражения в математике.
Числовые и алгебраические выражения и их преобразования.
Как работать с математическими выражениями?
Допустим, перед вами пример. Хоть простой, хоть суперсложный (уравнение, неравенство, интеграл, производная и т.д….). Допустими, вы не Витя Перестукин и с математикой на «ты». Сможете, глядя на пример, сразу дать ответ?
В 99% случаев — нет. Если вы не гений математической мысли, конечно.)
Почему? А потому, что вам, так или иначе, придётся решать этот пример. Что значит «решать»? Это значит, последовательно, шаг за шагом, этот пример упрощать, добираясь до окончательного ответа. Или, по-другому, преобразовывать. Естественно, все эти фокусы (т.е. преобразования) надо проделывать по определённым правилам математики. Вот насколько успешно вы проведёте эти самые преобразования, настолько вы и сильны в математике.)
Так вот, имейте в виду: если вы не умеете делать правильные преобразования выражений, в математике вы не сможете сделать НИЧЕГО. Вообще ничего. Грустная перспектива? Вот и я так думаю.
Чтобы нас с вами не постигла столь печальная участь, имеет смысл разобраться в этой теме. Тем более тема достаточно простая. Разберёмся?:)
Что такое выражение в математике?
2+3 — это математическое выражение. a 2 — b 2 — это математическое выражение. И здоровенная дробь, и интеграл, и даже одно число или одна буковка — это всё математические выражения.
состоит из двух математических выражений, соединённых знаком равенства «=» (равно).
x 2 -4x+4≤0 – это тоже два математических выражения, соединённых знаком «≤» (меньше либо равно).
Короче говоря, термин «математическое выражение» применяется, чаще всего, чтобы не мычать, как корова и не кукарекать, как петух…
Спросят у вас, к примеру, что такое разность квадратов двух выражений. Первый вариант ответа: «Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?»
А человек в теме уверенно и с блеском в глазах ответит: «Разность квадратов двух выражений — это математическое выражение, представляющее собой произведение разности этих выражений и их суммы»!
Или: что такое квадратный корень? Квадратный корень — это математическое выражение, состоящее из подкоренного выражения и знака корня (радикала).
Согласитесь, второй вариант ответа выглядит куда более солидно и научно.)
Вот в таких вопросах фраза «математическое выражение» очень и очень удобна. Чтобы не объясняться на пальцах, как иностранные туристы в экзотической стране.
Гораздо сложнее — это конкретные математические выражения и работа с ними. Это совершенно другое дело.
Дело всё в том, что у каждого вида математических выражений имеется свой набор правил и приёмов, которому необходимо следовать при работе с ними.
У чисел — свой набор, у буквенных выражений — свой, у дробей — свой, у всяких там синусов, логарифмов, производных, интегралов — свои наборы действий. В каких-то наборах эти правила похожи или даже совпадают, а где-то — кардинально отличаются. Но пугаться этих жутких слов не надо. Эти страшные понятия мы с вами обязательно освоим в соответствующих разделах. А здесь мы с вами поработаем только с двумя видами математических выражений. А именно — с числовыми выражениями и с алгебраическими выражениями.
Что такое числовое выражение?
Что такое числовое выражение? Всё проще пареной репы.) Числовое выражение — это какое-то выражение с числами. Да-да, всего-навсего. Математическое выражение, составленное из цифр, знаков действий, скобок, знаков равенства/неравенства — это всё числовые выражения.
10-6 — числовое выражение,
(3-2,1)·0,5 — числовое выражение.
Или даже вот эти монстры:
это всё числовые выражения.
Да, в последнем примере появились специальные математические символы — радикал, значок логарифма и значок синуса. Но в этом выражении тоже нет букв. Только числа! Это самое главное.
Короче говоря, любые числа, дроби, примеры на вычисление без иксов, игреков и прочих буковок — это всё числовые выражения. Намёк понятен?)
В чём главный признак числового выражения? В том, что в нём нет букв. Вообще никаких. Математические значки (если надо) — пожалуйста. А вот букв — нету. Это ключевой признак.)
Что же можно делать с числовыми выражениями? Числовые выражения, как правило, можно (и нужно) считать. Для этого, бывает, приходится менять знаки, раскрывать скобки (или наоборот, заключать в скобки), сокращать, выносить общий множитель, раскладывать на множители т.д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений — чуть позже. Терпение, друзья.)
А здесь мы с вами разберёмся с одним забавным случаем, когда с числовым выражением делать ничего не надо. Совсем! Эта приятная операция (ничего не делать)) производится, когда числовое выражение не имеет смысла.
Понятное дело, что если мы с вами напишем какую-то белиберду типа 4+)-(=), то делать ничего и не будем. Ибо непонятно, что с этим делать. Ну, разве посчитать количество скобочек.)
Однако, попадаются в математике и внешне вполне себе благопристойные выражения.
Однако это числовое выражение тоже не имеет смысла. Почему? А потому, что если выписать отдельно знаменатель дроби да посчитать, получается ноль. На который делить нельзя. Нет такой операции в математике!
И это выражение тоже не имеет смысла! Догадались? А вы посчитайте, что под корнем получится.) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике.
Конечно, чтобы сделать такое умозаключение, пришлось потрудиться и посчитать, что в знаменателе да под корнем получится. А в примерах может быть такого понаворочено, что… Тут уж ничего не поделаешь.)
Короче говоря, числовое выражение не имеет смысла тогда, когда в результате преобразований этого самого выражение получается запретное действие. Запретных действий в математике не так уж много: это деление на ноль, извлечение корня чётной степени из отрицательного числа, ограничения в логарифмах, в тригонометрии и в арках. Это обсуждается в соответствующих темах.
Итак, что такое числовое выражение — вникли (надеюсь).
Когда числовое выражение не имеет смысла — осознали.
Пора двигаться на следующий уровень.)
Что такое алгебраическое выражение?
Если в игру дополнительно вступают буквы, то выражение становится… Да! Оно становится алгебраическим выражением!
Понятие алгебраическое выражение — более широкое, чем числовое. Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение — это и алгебраическое выражение. Только без букв. Типа всякий русский — россиянин, но не всякий россиянин — русский.)
В выражении х+6, например, буква икс — переменная величина. Или коротко — переменная. В отличие от шестёрки, которая — величина постоянная. Или коротко — постоянная.
Что означает термин «алгебраическое выражение»? Он означает, что, в отличие от арифметики, (которая, как известно, работает только с числами), мы должны использовать законы и правила алгебры. Непонятно? Поясняю на несложном примере:
Что можно сделать? Посчитать и всего делов-то.) Слева шестёрка и справа тоже. А для каких-нибудь других чисел такое выполняется? Тоже можно посчитать и сравнить. Но чисел в математике — бесконечное количество. И что же? Каждый раз считать и сравнивать?!
А вот если мы шагнём из арифметики в алгебру и распишем данное равенство через алгебраические выражения:
то мы сразу решим все вопросы! Для всех чисел махом! Мощная штука — алгебра.)
А когда алгебраическое выражение не имеет смысла? Что такое ОДЗ?
С числовыми выражениями всё ясно. Там на ноль делить нельзя да корни извлекать из отрицательных чисел, ну и некоторые другие логарифмические/тригонометрические фишки. А тут как узнаешь, на что делим или из чего извлекаем…
Очень просто! Точно так же!
Возьмём, к примеру, алгебраическое выражение:
Имеет ли оно смысл? Бэ-то любое число… Любое-то любое… Но есть среди этого бесконечного набора чисел такое значение b, при котором это выражение точно не имеет смысла. Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят «подставить») на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички.
И вот этот самый весь остальной набор чисел, которые можно подставлять в данное выражение, и который не приводит к запретному действию, в математике называется областью допустимых значений (ОДЗ) выражения. В нашем примере областью допустимых значений (ОДЗ) служат все числа, кроме единички.
Видим квадратный корень. Сразу соображаем (из теории, т.е. основ), что корень квадратный извлекается только из положительных чисел и нуля. А вот из отрицательных — ни в какую!
Вот и обезопасим себя вот такой записью:
Таким образом, данный хитрое выражение имеет смысл лишь при иксах, больших (или равных) двойке. Число, скажем, 3, вполне себе прокатит, а вот ноль — никак нет: он меньше двойки. ОДЗ — штука жёсткая!
Уловили принцип? Внимательно смотрим на выражение с переменными, ищем опасные места и смотрим, при каких переменных получается запретная операция. И исключаем эти значения из ОДЗ.
А потом внимательно читаем задание. Чего хотят-то? Внимательное чтение никто не отменял, да… Если в задании спрашивают, при каких значениях переменной выражение имеет смысл, то ответом будут служить все значения, кроме запретных.
Или наоборот: при каких значениях переменных выражение не имеет смысла? Тогда найденные запретные значения и будут служить ответом к заданию. Почувствуйте разницу, что называется.)
А теперь вопрос к размышлению. А зачем нам смысл выражения? Есть он, нет его… Какая разница? Дело всё в том, что это понятие становится крайне важным в старших классах! Да и в ВУЗе тоже. Без этого важного понятия вы не сможете проделывать такие простые операции, как нахождение области определения функции, ОДЗ уравнений, неравенств. Что неизбежно будет приводить к полному провалу и непониманию всех этих серьёзных тем. Увы.)
Итак, самое главное из сегодняшнего урока:
1. Числовое выражение — это выражение с числами (т.е. без букв).
2. Если, помимо чисел, в выражении есть буквы, то оно называется алгебраическим выражением.
3. Как числовое, так и алгебраическое выражение, может иметь смысл, а может и не иметь. При встрече с алгебраическим выражением первым делом ищем его ОДЗ.
4. Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!
Ну а в различных видах преобразований выражений мы с вами подробненько разберёмся и плотно поработаем в следующих уроках этого раздела.)
Восемь крылатых фраз, которые мы не до конца понимаем
Однако существует много крылатых выражений, которые действительно были произнесены великими. Правда, знаем мы их в укороченном варианте или вырванными из контекста. Что они значат на самом деле?
«Цель оправдывает средства»
«О мертвых либо хорошо, либо ничего»
Изречение древнегреческого политика и поэта Хилона из Спарты (VI в. до н. э.), которое процитировал римский историк Диоген Лаэртский (III в. н. э.) в сочинении «Жизнь, учение и мнения прославленных философов». В оригинале фраза звучит так: «О мертвых либо хорошо, либо ничего, кроме правды». Есть разница, не так ли?
«Народ безмолвствует»
Цитата из Пушкина, которая считается символом смиренности и покорности русского народа. Но у Александра Сергеевича значение этой фразы совершенно обратное. Люди не боятся выразить протест новой власти и отказываются ее славить. Итак, в финале поэмы после кровавой расправы над Годуновыми народу представляют нового царя. И вот что происходит.
Народ в ужасе молчит.
Мосальский: Что ж вы молчите? Кричите: да здравствует царь Димитрий Иванович!
«Любви все возрасты покорны»
Отрывок из пушкинского «Евгения Онегина» можно использовать как визитную карточку пар, состоящих в неравном браке. Особенно, когда богатенький дядя в возрасте берет в жены юную прекрасную нимфу. Но классик имел в виду совсем другое. Открываем книгу:
Любви все возрасты покорны;
Но юным, девственным сердцам
Ее порывы благотворны,
Как бури вешние полям:
В дожде страстей они свежеют,
И жизнь могущая дает
И пышный цвет, и сладкий плод.
Но в возраст поздний и бесплодный,
На повороте наших лет,
Печален страсти мертвой след:
Так бури осени холодной
В болото обращают луг
И обнажают лес вокруг.
Седовласые поклонники молоденьких прелестниц, кажется, остались без красивых аргументов.
«Исключения подтверждают правила»
«Истина в вине»
Любимый афоризм алкоголиков. Мол, еще в Древнем Риме наливали и приговаривали! В действительности писатель Плиний Старший (I век н. э.) высказался так: «In vino veritas, in aqua sanitas», то есть «истина в вине, а здоровье в воде».
«В здоровом теле здоровый дух»
Неизвестно, кто и когда неправильно интерпретировал фразу римского поэта Ювенала, но в оригинале его цитата звучит так: «Надо молить богов, чтобы дух здоровый был в теле здоровом». Древний классик подразумевал, что тело и душа не связаны между собой. И что работать над недостатками своего поведения гораздо сложнее, чем над физической формой. Иными словами, если ты качок или девушка модельной внешности, совершенно необязательно, что у тебя ангельский характер.
Шопоголиком стал из-за фамилии?
Ученые рассказали, как имя влияет на судьбу
Исследователям из Соединенных Штатов удалось доказать, что имя, которое ребенок получает при рождении, способно серьезно повлиять на всю его жизнь. Речь идет прежде всего о таких моментах, как отношение к деньгам, любовь и трудоустройство с дальнейшим карьерным ростом.
Человеку с простым именем намного легче налаживать контакт с окружающими и находить работу. Он подсознательно вызывает у собеседника симпатию. (Подобное, к слову, распространяется и на названия компаний: чем проще звучит, тем больше у организации шансов на коммерческий успех).
Если верить еще одному исследованию, проведенному учеными из Шиппенбургского университета, редкие имена имеют серьезный недостаток: их обладатели значительно чаще уже в юном возрасте склонны нарушать закон. Скорее всего, это связано с тем, что такие дети с большим трудом находят себе друзей. Это делает их несколько асоциальными.