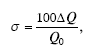О чем свидетельствует случайная погрешность

14. Виды погрешностей

14. Виды погрешностей

Выделяют следующие виды погрешностей:

1) абсолютная погрешность;

2) относительна погрешность;

3) приведенная погрешность;

4) основная погрешность;

5) дополнительная погрешность;

6) систематическая погрешность;

7) случайная погрешность;

8) инструментальная погрешность;

9) методическая погрешность;

10) личная погрешность;

11) статическая погрешность;

12) динамическая погрешность.

Погрешности измерений классифицируются по следующим признакам.

По способу математического выражения погрешности делятся на абсолютные погрешности и относительные погрешности.

По взаимодействию изменений во времени и входной величины погрешности делятся на статические погрешности и динамические погрешности.

По характеру появления погрешности делятся на систематические погрешности и случайные погрешности.

По характеру зависимости погрешности от влияющих величин погрешности делятся на основные и дополнительные.

По характеру зависимости погрешности от входной величины погрешности делятся на аддитивные и мультипликативные.

Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.

Абсолютная погрешность вычисляется по следующей формуле:

где AQ n – абсолютная погрешность;

Q n – значение некой величины, полученное в процессе измерения;

Q 0 – значение той же самой величины, принятое за базу сравнения (настоящее значение).

Абсолютная погрешность меры – это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины.

Относительная погрешность – это число, отражающее степень точности измерения.

Относительная погрешность вычисляется по следующей формуле:

Q 0 – настоящее (действительное) значение измеряемой величины.

Относительная погрешность выражается в процентах.

Приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.

Нормирующее значение определяется следующим образом:

1) для средств измерений, для которых утверждено номинальное значение, это номинальное значение принимается за нормирующее значение;

2) для средств измерений, у которых нулевое значение располагается на краю шкалы измерения или вне шкалы, нормирующее значение принимается равным конечному значению из диапазона измерений. Исключением являются средства измерений с существенно неравномерной шкалой измерения;

3) для средств измерений, у которых нулевая отметка располагается внутри диапазона измерений, нормирующее значение принимается равным сумме конечных численных значений диапазона измерений;

4) для средств измерения (измерительных приборов), у которых шкала неравномерна, нормирующее значение принимается равным целой длине шкалы измерения или длине той ее части, которая соответствует диапазону измерения. Абсолютная погрешность тогда выражается в единицах длины.

Погрешность измерения включает в себя инструментальную погрешность, методическую погрешность и погрешность отсчитывания. Причем погрешность отсчитывания возникает по причине неточности определения долей деления шкалы измерения.

Инструментальная погрешность – это погрешность, возникающая из—за допущенных в процессе изготовления функциональных частей средств измерения ошибок.

Методическая погрешность – это погрешность, возникающая по следующим причинам:

1) неточность построения модели физического процесса, на котором базируется средство измерения;

2) неверное применение средств измерений.

Субъективная погрешность – это погрешность возникающая из—за низкой степени квалификации оператора средства измерений, а также из—за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.

Погрешности по взаимодействию изменений во времени и входной величины делятся на статические и динамические погрешности.

Статическая погрешность – это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.

Динамическая погрешность – это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).

По характеру зависимости погрешности от влияющих величин погрешности делятся на основные и дополнительные.

Основная погрешность – это погрешность, полученная в нормальных условиях эксплуатации средства измерений (при нормальных значениях влияющих величин).

Дополнительная погрешность – это погрешность, которая возникает в условиях несоответствия значений влияющих величин их нормальным значениям, или если влияющая величина переходит границы области нормальных значений.

Нормальные условия – это условия, в которых все значения влияющих величин являются нормальными либо не выходят за границы области нормальных значений.

Рабочие условия – это условия, в которых изменение влияющих величин имеет более широкий диапазон (значения влияющих не выходят за границы рабочей области значений).

Рабочая область значений влияющей величины – это область значений, в которой проводится нормирование значений дополнительной погрешности.

По характеру зависимости погрешности от входной величины погрешности делятся на аддитивные и мультипликативные.

Аддитивная погрешность – это погрешность, возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (абсолютного).

Мультипликативная погрешность – это погрешность, изменяющаяся вместе с изменением значений величины, подвергающейся измерениям.

Надо заметить, что значение абсолютной аддитивной погрешности не связано со значением измеряемой величины и чувствительностью средства измерений. Абсолютные аддитивные погрешности неизменны на всем диапазоне измерений.

Значение абсолютной аддитивной погрешности определяет минимальное значение величины, которое может быть измерено средством измерений.

Значения мультипликативных погрешностей изменяются пропорционально изменениям значений измеряемой величины. Значения мультипликативных погрешностей также пропорциональны чувствительности средства измерений Мультипликативная погрешность возникает из—за воздействия влияющих величин на параметрические характеристики элементов прибора.

Погрешности, которые могут возникнуть в процессе измерений, классифицируют по характеру появления. Выделяют:

1) систематические погрешности;

2) случайные погрешности.

В процессе измерения могут также появиться грубые погрешности и промахи.

Систематическая погрешность – это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины. Обычно систематическую погрешность пытаются исключить возможными способами (например, применением методов измерения, снижающих вероятность ее возникновения), если же систематическую погрешность невозможно исключить, то ее просчитывают до начала измерений и в результат измерения вносятся соответствующие поправки. В процессе нормирования систематической погрешности определяются границы ее допустимых значений. Систематическая погрешность определяет правильность измерений средств измерения (метрологическое свойство).

Систематические погрешности в ряде случаев можно определить экспериментальным путем. Результат измерений тогда можно уточнить посредством введения поправки.

Способы исключения систематических погрешностей делятся на четыре вида:

1) ликвидация причин и источников погрешностей до начала проведения измерений;

2) устранение погрешностей в процессе уже начатого измерения способами замещения, компенсации погрешностей по знаку, противопоставлениям, симметричных наблюдений;

3) корректировка результатов измерения посредством внесения поправки (устранение погрешности путем вычислений);

4) определение пределов систематической погрешности в случае, если ее нельзя устранить.

Ликвидация причин и источников погрешностей до начала проведения измерений. Данный способ является самым оптимальным вариантом, так как его использование упрощает дальнейший ход измерений (нет необходимости исключать погрешности в процессе уже начатого измерения или вносить поправки в полученный результат).

Для устранения систематических погрешностей в процессе уже начатого измерения применяются различные способы

Способ введения поправок базируется на знании систематической погрешности и действующих закономерностей ее изменения. При использовании данного способа в результат измерения, полученный с систематическими погрешностями, вносят поправки, по величине равные этим погрешностям, но обратные по знаку.

Способ замещения состоит в том, что измеряемая величина заменяется мерой, помещенной в те же самые условия, в которых находился объект измерения. Способ замещения применяется при измерении следующих электрических параметров: сопротивления, емкости и индуктивности.

Способ компенсации погрешности по знаку состоит в том, что измерения выполняются два раза таким образом, чтобы погрешность, неизвестная по величине, включалась в результаты измерений с противоположным знаком.

Способ противопоставления похож на способ компенсации по знаку. Данный способ состоит в том, что измерения выполняют два раза таким образом, чтобы источник погрешности при первом измерении противоположным образом действовал на результат второго измерения.

Случайная погрешность – это составная часть погрешности результата измерения, изменяющаяся случайно, незакономерно при проведении повторных измерений одной и той же величины. Появление случайной погрешности нельзя предвидеть и предугадать. Случайную погрешность невозможно полностью устранить, она всегда в некоторой степени искажает конечные результаты измерений. Но можно сделать результат измерения более точным за счет проведения повторных измерений. Причиной случайной погрешности может стать, например, случайное изменение внешних факторов, воздействующих на процесс измерения. Случайная погрешность при проведении многократных измерений с достаточно большой степенью точности приводит к рассеянию результатов.

Промахи и грубые погрешности – это погрешности, намного превышающие предполагаемые в данных условиях проведения измерений систематические и случайные погрешности. Промахи и грубые погрешности могут появляться из—за грубых ошибок в процессе проведения измерения, технической неисправности средства измерения, неожиданного изменения внешних условий.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

Виды пиломатериалов

Виды пиломатериалов Чаще всего в магазинах и на лесобазах продается уже высушенная древесина, а сырая встречается довольно редко. В зависимости от того, что вы хотите сделать и на что вам понадобилась древесина, вы можете приобрести кряж (целые стволы дерева или длинные

Виды пиломатериалов

Виды пиломатериалов В зависимости от назначения элемента конструкции, для которого используется тот или иной пиломатериал, необходимо определять и его размеры:– для стропил, балок цокольных и междуэтажных перекрытий, а также проступей ступеней лестниц и наружных

Виды пиломатериалов

Виды пиломатериалов В зависимости от назначения элемента конструкции, для которого используется тот или иной пиломатериал, необходимо определять и его размеры:– для стропил, балок цокольных и междуэтажных перекрытий, а также проступей ступеней лестниц и наружных

Виды соединений

Виды соединений Все соединения, будь то плотничные или столярные, называются посадками, потому что в их основе лежит принцип насаживания детали с шипом на деталь с пазом. В зависимости от того, как плотно соприкасаются детали в креплении, все посадки разделяются на

5.4 Виды проборок

5.4 Виды проборок Проборки, применяемые в ткачестве очень разнообразны. Их разнообразие определяется соотношением трех величин: Ro переплетения, Rnp. и количеством ремизок К.Рассмотрим пример, когда Ro = К = Rnp. В этом случае нити основы подряд пробираются в каждую ремизку и

14. Виды погрешностей

14. Виды погрешностей Выделяют следующие виды погрешностей:1) абсолютная погрешность;2) относительна погрешность;3) приведенная погрешность;4) основная погрешность;5) дополнительная погрешность;6) систематическая погрешность;7) случайная

19. Методы определения и учета погрешностей

19. Методы определения и учета погрешностей Методы определения и учета погрешностей измерений используются для того, чтобы:1) на основании результатов измерений получить настоящее (действительное) значение измеряемой величины;2) определить точность полученных

6. Виды стандартов

6. Виды стандартов Выделяют несколько видов стандартов. Применение в конкретной ситуации того или иного стандарта определяется характерными чертами и спецификой объекта стандартизации.Основополагающие стандарты – нормативные документы, утвержденные для

19. Методы определения и учета погрешностей

19. Методы определения и учета погрешностей Методы определения и учета погрешностей измерений используются для того, чтобы:1) на основании результатов измерений получить настоящее (действительное) значение измеряемой величины;2) определить точность полученных

38. Виды стандартов

38. Виды стандартов Выделяют несколько видов стандартов.Основополагающие стандарты – нормативные документы, утвержденные для определенных областей науки, техники и производства, содержащие в себе общие положения, принципы, правила и нормы для данных областей. Этот тип

3. виды веревки

3. виды веревки Основная отличительная черта, определяющая вид данной веревки, ее динамические качества, которые в основном зависят от ее способности удлиняться под нагрузкой. Еще при конструировании веревки в зависимости от желаемых эксплуатационных свойств ее

6.1. Виды иллюстраций

6.1. Виды иллюстраций ОСТ 29.130—97 «Издания. Термины и определения» так опре–деляет термин «иллюстрация» – изображение, поясняющее или дополняющее основной текст, помещенное на страницах и других элементах материальной конструкции издания.По методу отображения

50. Причины начальных погрешностей

50. Причины начальных погрешностей Начальные погрешности в измерение могут вноситься по следующим причинам.1.Удельный вес:1) степень однородности среды нарушена вследствие нахождения в ней примесей (в том числе и растворимых газов; такие жидкостные среды в гидравлике

1.5. Виды искусства

1.5. Виды искусства В процессе исторического развития искусства сложились различные его виды. Эпохи наивысшего расцвета искусства свидетельствуют о том, что полнота отображения мира достигается одновременным расцветом всех искусств. Как известно. Виды искусства можно

Виды ремонта

Виды ремонта В результате работы автомобиля, детали и узлы постепенно изнашиваются, в результате чего меняются их технические характеристики: увеличиваются зазоры между сопряженными деталями, повышается расход эксплуатационных материалом (топлива, масла, воды и

Источник

Погрешность измерений. Классификация

Погрешность средств измерения и результатов измерения.

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Инструментальные и методические погрешности.

Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.

Систематическая и случайная погрешности.

Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Причинами возникновения систематических составляющих погрешности измерения являются:

Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.

Погрешности адекватности и градуировки.

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

Абсолютная, относительная и приведенная погрешности.

Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.

Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.

Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

Аддитивные и мультипликативные погрешности.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).

Источник

Глава 1 Измерения и погрешности

1.1 Результат измерения

Рассмотрим простейший пример: измерение длины стержня с помощью линейки. Линейка проградуирована производителем с помощью некоторого эталона длины — таким образом, сравнивая длину стержня с ценой деления линейки, мы выполняем косвенное сравнение с общепринятым стандартным эталоном.

Во-вторых, мы никак не можем быть уверенны, что длина стержня на самом деле такова хотя бы с точностью до ошибки округления. Действительно, мы могли приложить линейку не вполне ровно; сама линейка могла быть изготовлена не вполне точно; стержень может быть не идеально цилиндрическим и т.п.

И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной точности измерения, теряет смысл само понятие «длины стержня». Ведь на масштабах атомов у стержня нет чётких границ, а значит говорить о его геометрических размерах в таком случае крайне затруднительно!

Она показывает, насколько погрешность мала по сравнению с самой измеряемой величиной (её также можно выразить в процентах: ε = δ ⁢ x x ⋅ 100 % ).

О необходимости оценки погрешностей.

Измерим длины двух стержней x 1 и x 2 и сравним результаты. Можно ли сказать, что стержни одинаковы или различны?

В физическом эксперименте (в том числе лабораторном практикуме) оценка погрешностей должна проводиться всегда (даже когда составители задания забыли упомянуть об этом).

1.2 Многократные измерения

Проведём серию из n одинаковых ( однотипных ) измерений одной и той же физической величины (например, многократно приложим линейку к стержню) и получим ряд значений

Что можно сказать о данном наборе чисел и о длине стержня? И можно ли увеличивая число измерений улучшить конечный результат?

По набору результатов 𝐱 можно вычислить их среднее арифметическое:

Это значение, вычисленное по результатам конечного числа n измерений, принято называть выборочным средним. Здесь и далее для обозначения выборочных средних будем использовать угловые скобки.

Кроме среднего представляет интерес и то, насколько сильно варьируются результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как

Разброс данных относительно среднего принято характеризовать среднеквадратичным отклонением :

Будем увеличивать число измерений n ( n → ∞ ). Если объект измерения и методика достаточно стабильны, то отклонения от среднего Δ ⁢ x i будут, во-первых, относительно малы, а во-вторых, положительные и отрицательные отклонения будут встречаться примерно одинаково часто. Тогда при вычислении ( 1.1 ) почти все отклонения Δ ⁢ x i скомпенсируются и можно ожидать, что выборочное среднее при n ≫ 1 будет стремиться к некоторому пределу:

Тогда предельное значение x ¯ можно отождествить с «истинным» средним для исследуемой величины.

Предельную величину среднеквадратичного отклонения при n → ∞ обозначим как

Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр меняется во времени или в результате самого измерения, либо испытывает слишком большие случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не останавливаемся.

Многие случайные величины подчиняются так называемому нормальному закону распределения (подробнее см. Главу 2 ). Для таких величин могут быть строго доказаны следующие свойства:

1.3 Классификация погрешностей

Чтобы лучше разобраться в том, нужно ли многократно повторять измерения, и в каком случае это позволит улучшить результаты опыта, проанализируем источники и виды погрешностей.

В первую очередь, многократные измерения позволяют проверить воспроизводимость результатов: повторные измерения в одинаковых условиях, должны давать близкие результаты. В противном случае исследование будет существенно затруднено, если вообще возможно. Таким образом, многократные измерения необходимы для того, чтобы убедиться как в надёжности методики, так и в существовании измеряемой величины как таковой.

При любых измерениях возможны грубые ошибки — промахи ( англ. miss). Это «ошибки» в стандартном понимании этого слова — возникающие по вине экспериментатора или в силу других непредвиденных обстоятельств (например, из-за сбоя аппаратуры). Промахов, конечно, нужно избегать, а результаты таких измерений должны быть по возможности исключены из рассмотрения.

Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма непрост. В литературе существуют статистические критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем пользоваться (по крайней мере, без серьезного понимания последствий такого отбора). Отбрасывание аномальных данных может, во-первых, привести к тенденциозному искажению результата исследований, а во-вторых, так можно упустить открытие неизвестного эффекта. Поэтому при научных исследованиях необходимо максимально тщательно проанализировать причину каждого промаха, в частности, многократно повторив эксперимент. Лишь только если факт и причина промаха установлены вполне достоверно, соответствующий результат можно отбросить.

Кроме того, удобно разделять погрешности по их происхождению. Можно выделить

Замечание. Разделение погрешностей на систематические и случайные не является однозначным и зависит от постановки опыта. Например, производя измерения не одним, а несколькими однотипными приборами, мы переводим систематическую приборную ошибку, связанную с неточностью шкалы и калибровки, в случайную. Разделение по происхождению также условно, поскольку любой прибор подвержен воздействию «естественных» случайных и систематических ошибок (шумы и наводки, тряска, атмосферные условия и т. п.), а в основе работы прибора всегда лежит некоторое физическое явление, описываемое не вполне совершенной теорией.

1.3.1 Случайные погрешности

Случайный характер присущ большому количеству различных физических явлений, и в той или иной степени проявляется в работе всех без исключения приборов. Случайные погрешности обнаруживаются просто при многократном повторении опыта — в виде хаотичных изменений ( флуктуаций ) значений < x i >.

Если случайные отклонения от среднего в большую или меньшую стороны примерно равновероятны, можно рассчитывать, что при вычислении среднего арифметического ( 1.1 ) эти отклонения скомпенсируются, и погрешность результирующего значения » display=»inline»> ⟨ x ⟩ будем меньше, чем погрешность отдельного измерения.

Случайные погрешности бывают связаны, например,

с особенностями используемых приборов : техническими недостатками (люфт в механических приспособлениях, сухое трение в креплении стрелки прибора), с естественными (тепловой и дробовой шумы в электрических цепях, тепловые флуктуации и колебания измерительных устройств из-за хаотического движения молекул, космическое излучение) или техногенными факторами (тряска, электромагнитные помехи и наводки);

с особенностями и несовершенством методики измерения (ошибка при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером);

с несовершенством объекта измерений (неровная поверхность, неоднородность состава);

со случайным характером исследуемого явления (радиоактивный распад, броуновское движение).

1.3.2 Систематические погрешности

Систематические погрешности, в отличие от случайных, невозможно обнаружить, исключить или уменьшить просто многократным повторением измерений. Они могут быть обусловлены, во-первых, неправильной работой приборов ( инструментальная погрешность ), например, сдвигом нуля отсчёта по шкале, деформацией шкалы, неправильной калибровкой, искажениями из-за не нормативных условий эксплуатации, искажениями из-за износа или деформации деталей прибора, изменением параметров прибора во времени из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации результатов ( методическая погрешность ), например, из-за использования слишком идеализированной физической модели явления, которая не учитывает некоторые значимые факторы (так, при взвешивании тел малой плотности в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических цепях может быть необходим учет неидеальности амперметров и вольтметров и т. д.).

Систематические погрешности условно можно разделить на следующие категории.

Известные погрешности, которые могут быть достаточно точно вычислены или измерены. При необходимости они могут быть учтены непосредственно: внесением поправок в расчётные формулы или в результаты измерений. Если они малы, их можно отбросить, чтобы упростить вычисления.

Погрешности известной природы, конкретная величина которых неизвестна, но максимальное значение вносимой ошибки может быть оценено теоретически или экспериментально. Такие погрешности неизбежно присутствуют в любом опыте, и задача экспериментатора — свести их к минимуму, совершенствуя методики измерения и выбирая более совершенные приборы.

Чтобы оценить величину систематических погрешностей опыта, необходимо учесть паспортную точность приборов (производитель, как правило, гарантирует, что погрешность прибора не превосходит некоторой величины), проанализировать особенности методики измерения, и по возможности, провести контрольные опыты.

Погрешности известной природы, оценка величины которых по каким-либо причинам затруднена (например, сопротивление контактов при подключении электронных приборов). Такие погрешности должны быть обязательно исключены посредством модификации методики измерения или замены приборов.

Наконец, нельзя забывать о возможности существования ошибок, о которых мы не подозреваем, но которые могут существенно искажать результаты измерений. Такие погрешности самые опасные, а исключить их можно только многократной независимой проверкой измерений, разными методами и в разных условиях.

В учебном практикуме учёт систематических погрешностей ограничивается, как правило, паспортными погрешностями приборов и теоретическими поправками к упрощенной модели исследуемого явления.

Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.

Источник