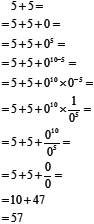Ноль в нулевой степени чему равно и почему

Ноль в степени ноль

Ноль — наверное самое загадочное число и самое контринтуитивное. Ведь его аналога в реальной жизни просто нет. Ноль — это отсутствие чего-то. Но почему ноль в степени ноль равняется единице? И главный вопрос, так ли это на самом деле? Можете проверить на своем калькуляторе до того, как прочтете…

Ноль «в степени» ноль

Как такое может быть? А вот как: 1 0 =1, 2 0 =1…. х 0 =1. Любое число при взведении в нулевую степени равняется единице. Чем сам ноль хуже? Но не все так просто.

Что означает возвести в степень? Например «два в квадрате». Что мы делаем, мы двойку умножаем на саму себя 2 раза (2*2=4), «два в кубе», двойку умножаем саму на себя 3 раза (2*2*2=8). А что если степень, это «ноль»? Нужно взять число и умножить само на себя…. ноль раз? Это странно.

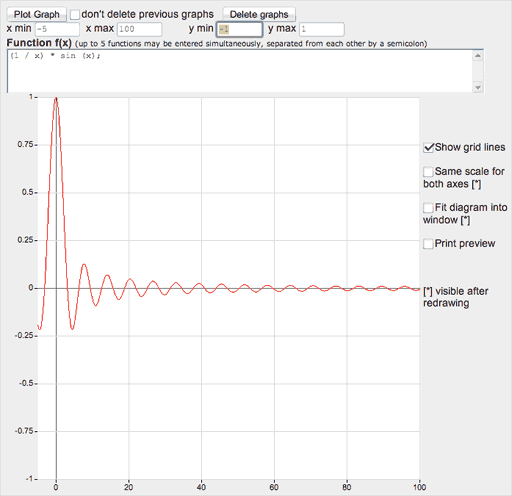
Вот как выглядит график функции y=x x

Видно, что при уменьшении значения Х значение У сначала снижается, а потом начинает расти и превращается… в единицу при условии очень маленьких (почти нулевых) значениях Х. Было бы логично предположить, что когда значение уменьшится до ноля, там тоже будет единица.

Еще раз, вернемся к простым цифрам:

Что означает эта запись? Чтобы получить девять, нужно тройку умножить два раза. Правда же?

Сколько раз нужно умножить тройку саму на себя, чтобы получить единицу? А если разделить 1 на 3? Простого ответа нет? Логично, что чем больше значение степени, тем больше результат, и чем меньше это значение, тем и результат меньше.

Но на графике выше показано, что кривая «упирается» в предел, в единицу. Точнее, значение функции становится равным 1, когда ноль еще даже не достигнут. И если уменьшать Х еще больше, все равно, дальше единицы не сдвинуться.

Контекст

Как получается, что при умножении ноля самого на себя получается что-то большее самого ноля?

Если мы в реальной жизни (а не в математике) съели все яблоки и их у нас 0, то сколько бы мы не умножали отсутствующие яблоки на такие же «нулевые» фрукты, как может у нас возникнуть целое яблоко? Если вам кажется такой вопрос простым, так и есть.

С одной точки зрения это странное выражение будет равняться единице, а вот с другой оно будет «не определено». То есть никакой единицы а результате умножения ноля на ноль и быть не может, да?

Математика говорит, что:

3 2 ×3 2 это тоже самое, что и 3 2+2 = 3 4 = 3 × 3 × 3 × 3= 81

4 5 ÷4 3 это тоже самое, что и 4 5–3 = 4 2 = 4 × 4 = 16

Тогда, если степени одинаковы:

3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 = Ой?!

Но ведь мы можем и не вычитать степени, а просто сделать две операции отдельно:

3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 , но 3 2 =9, тогда 3 2 ÷3 2 = 3 2-2 или 3 2 ÷3 2 =9÷9=1

А что будет если одно число поделить на самого себя? Единица!

Матанализ

С точки зрения математического анализа, все одновременно и сложно, и совсем просто. Ноль в степени ноль = неопределенность. Что, согласитесь, более логично. Ведь если у нас нет ничего и мы ничего умножим само на себя, не может же возникнуть что-то из этой пустоты?

Теория множеств

Давайте посмотрим с точки зрения теории множеств. Допустим, у нас есть два множества.

Первое множество, это количество символов пароля, которым закрыт доступ к вашей страничке в соцсети, или, еще лучше, PIN код банковской карты допустим — 4 символа.

Второе множество, это количество значений, корыте может принимать каждый символ. Предположим, что это только цифры, значит цифр — 10.

Вопрос, сколько вариантов комбинаций существует? Сколько раз нужно ввести случайную комбинацию, чтобы угадать пароль? Каждый символ:

10 4 =10 000 тысяч вариантов.

Можно сказать, что множество цифр (10) отображается на множестве возможных символов (4). Но есть и «пустые» множества. Например, вы не поставили пароль вовсе, у вас ноль символов, которые можно угадать, так сколько попыток понадобится, чтобы получить доступ к счету? Ровно одна.

То есть при 10 0 =1, но тоже самое случится, если пароля нет и значений тоже нет 0 0 =1. Простыми словами, ноль в степени ноль, означает, что пароль не установлен и каждое значение тоже 0. Тогда может существовать только одна такая «комбинация».

А на самом деле?

Практического применения это математическое выражение, как нетрудно догадаться, не имеет вовсе. Ни одном инженеру, ни одному экономисту не придет в голову умножать ноль на ноль ноль раз. Это просто не применимая конструкция. Так что вопрос остается в области математики, и может быть философии.

Это наверное единственный случай, когда оставаясь математиком можно для свободно для себя решать чему равно «0 в степени 0».

Источник

Better Explained: Как понять ноль в нулевой степени?

Как мы можем повторить ноль нулевое количество раз и получить единицу? Всё дело в том, что наш подход к степени числа как к многократному умножению неверен. Нам нужно сменить парадигму. Давайте посмотрим, как мы привыкли воспринимать арифметические действия, и что они на самом деле из себя представляют.

Сложение

Как мы привыкли думать: это повторяющийся счёт

Как на самом деле: перемещение

Умножение

Как мы привыкли думать: это многократное сложение

Как на самом деле: масштабирование

Степень

Как мы привыкли думать: многократное умножение

Как на самом деле: рост с течением времени

Смотрим на арифметику как на преобразование

Отойдём на шаг назад. Как мы изучаем арифметику? Нас учат, что числа — это некое количество единиц; сложение — это прибавление одного количества единиц к другому количеству единиц (3+4 = 7), а умножение — это многократное сложение (2*3 = 2+2+2 = 6).

Очевидно, что эта модель восприятия неполноценна. Числа — это не просто единицы чего-то; гораздо лучше представлять их как некие точки с определённым положением на линии. Положение может быть отрицательным (-1), либо между другими числами (2²), либо в другом измерении (i).

Таким образом арифметика предстаёт перед нами как способ преобразовывать число. Сложение становится перемещением (+3 — это перемещение на 3 единицы вправо); умножение становится масштабированием (*3 — это увеличить число в три раза).

А что же такое тогда степень числа?

Познакомьтесь с Экпандотроном™

Это Экспандотрон 3000. Он выглядит как достаточно потрёпанная микроволновка, но вместо подогрева пищи она занимается ростом чисел. Просто положите число внутрь и проделайте несколько простых операций.

Вуаля! После звукового сигнала достаём наше новенькое готовое число. Например, мы хотим изменить 1 на 9. Что нам нужно сделать?

Что мы видим? Мы видим, как число начинает преобразовываться: 1; 1,1; 1,2. По окончании первой секунды оно уже выглядит как 3 и продолжает меняться: 3,1; 3,5; 4,0; 6,0; 7,5. И по окончании второй секунды оно превратилось в 9.

В математическом представлении Экспандотрон (или показательная функция) делает для нас следующее:

Например, 3 2 = 9/1. Основанием является то количество раз, в которое нам нужно вырастить число (х3), а степенью — количество времени (2). Формула типа 2 n означает «Используйте свой Экспандотрон на мощности х2 в течение n секунд».

Работу Экспандотрона мы всегда начинаем с 1, чтобы посмотреть, как он меняет одну единицу. Если мы хотим посмотреть, что случится с 3 в Экспандотроне, мы просто масштабируем конечный результат. Например:

Начните с 1 и умножьте на двойку в третьей степени: 1*2 3 = 1 * 2 * 2 * 2 = 8

Начните с 3 и умножьте на двойку в третьей степени: 3*2 3 = 3 * 2 * 2 * 2 = 24

Каждый раз, когда вы видите простую степень, вы начинаете с 1.

Идём к пониманию масштабирующего множителя

При умножении мы можем просто указать конечный масштабирующий множитель. Хотите число в 8 раз больше? Умножаем на 8. Готово.

Степени более капризны в обращении. Вот как они работают:

Вы: Хочу вырастить вот это число.

Экспандотрон: Ок, давай его сюда.

Вы: И насколько большим оно станет?

Экспандотрон: Пффф, без понятия. Давай посмотрим.

Вы: Посмотрим? Я думал, ты зна.

Экспандотрон: Тихо! Оно растёт! Растёт!

Экспандотрон: Готово! Это шедевр!

Это может звучать раздражающе неопределённо, но знаете, что? Большинство явлений природы заканчиваются неизвестно чем!

Как думаете, бактерия действительно планирует делиться каждые 14 часов? Нет, она просто питается забытым вами в холодильнике хлебом и растёт так быстро, как только может. Чтобы предсказать поведение этой бактерии, мы можем лишь использовать значения темпа её роста и длительности роста — и только потом мы получим конечное значение.

Иными словами, степень числа — это такой способ сказать «Начинаем с таких условий, изменяем их и смотрим, к чему мы придём». Этим и занимается наш Экспандотрон.

Идём к пониманию дробных степеней

Очень легко запутаться, если мы думаем о двойке в полуторной степени привычным способом — как о многократном умножении. Но в Экспандотроне всё просто: 1,5 — это всего лишь проведённое в нём время.

2 1,5 означает 1,5 секунды в машине, значит, этот рост окажется где-то между двукратным и четырёхкратным.

Умножение степеней

Что если мы захотим прогнать два цикла роста один за другим? Ну, например, мы используем машину в течение 2 секунд, а потом ещё 3 секунды на той же мощности:

Представьте самую обычную микроволновку. Разве это не будет самый обычный цикл длительностью в 5 секунд? Будет. Здесь происходит то же самое — раз уже мощность (основание) остаётся одинаковой, мы просто складываем время:

Квадратные корни

Продолжим. Предположим, мы выбрали мощность а и устанавливаем рост в течение 3 секунд:

Неплохо. Как будет выглядеть рост в течение половины этого времени? Логично, что 1,5 секунды.

А если мы проделаем то же самое два раза?

частичный рост * частичный рост = полный рост

Смотрим на это уравнение и видим, что «частичный рост» — это квадратный корень из значения полного роста. А если мы разделим время на три части?

частичный рост * частичный рост * частичный рост = полный рост

А вот и кубический корень! Это даёт нам интуитивное понимание того, почему деление степеней даёт нам корни: мы разбиваем время на равные доли.

Отрицательные степени

А как быть с отрицательными степенями? Отрицательные степени для нас будут значить обратный отсчёт во времени. Если движение вперёд во времени приводит нас к росту, движение назад, скорее всего, выльется в уменьшение числа.

Это значит следующее: «Секунду назад у нас была половина от текущего количества (1/2 1 ). Любой график экспоненциального роста строится именно так.

Выберите точку на шкале времени, например, 3,5 секунды (2 3,5 = 11,3). Через секунду мы удвоим наше количество (2 4,5 = 22,5). А секунду назад у нас была всего лишь половина от текущего количества (2 2,5 = 5,65).

Приходим к нулевой степени

Значит, масштабирующий множитель равен единице, значит, никаких изменений с нашим числом не происходит. Новое число будет равняться исходному числу, то есть (вы же помните, что исходное число у нас единица?) единице. Масштабирования не происходит.

Приходим к нулевому основанию

Приходим к нулевому основанию в нулевой степени

0 в степени 0 означает рост х0 в течение 0 секунд. Хоть мы и планировали аннулировать число, мы так и не запустили машину. Новое число равно исходному числу (то есть в наш Экспандотрон мы положили единицу), масштабирующий множитель тоже равен единице.

Конечно, Экспандотрона на самом деле не существует (а жаль!). Конечно, числа на самом деле не выстраиваются в линейку — они всего лишь один из множества способов взглянуть на мир.

По материалам очаровательной статьи на Better Explained.

Источник

Почему 0 в степени 0 равно 1?

Ноль в степени ноль является неопределенным выражением.
Это выражение может быть равно чему угодно в зависимости от скорости направления предельного перехода к нулю.

Однако, некоторые авторы предлагают принять соглашение о том, что 0^0=1. В пользу подобного варианта приводятся несколько доводов. Например, разложение в ряд экспоненты и другие.

Дискуссия по поводу определения продолжается, по крайней мере, с начала XIX века и ДО СИХ ПОР. В начале 19-го века математики считали, что 0^0=1, но в 1821 году Коши причислил 0^0 к неопределённостям, таким, как, например, 0/0.

Сайт MathWorld считает, что 0^0 считается неопределённым, несмотря на то, что соглашение 0^0=1 позволяет в некоторых случаях упростить запись некоторых формул. В России Большая российская энциклопедия, Большая советская энциклопедия, Математический энциклопедический словарь, Справочник по элементарной математике Выгодского, школьные учебники и другие источники однозначно характеризуют 0^0 как выражение, не имеющее смысла (неопределённость).

Интересно, что в компьютерных языках программирования, при использовании функции возведения в целую степень, 0^0 всегда дает результат равный 1. Но такой же результат будет не только для нуля, но и для NaN и для бесконечность. То есть, это чисто так устроена функция возведения в целую степень.
А вот функция возведения в нецелую степень уже дает результат NaN, то есть неопределенность.
А в тех языках программирования, где нет разделения функции возведения в степень на функцию для целого и вещественного показателя, там всё по разному. Например, в C++ выдает единицу.

Источник

Ноль в нулевой степени чему равно и почему

Ноль в степени ноль равно нулю. Я знаком с методами как доказывают обратное. Все они не приемлемы. Вот внизу ролик поставили. Человек вычитывает степень числа которое приближается к нулю. Итог приближается к единице. Но во первых это не ноль, на самом деле это бесконечность. Ибо число приближается к нулю бесконечно. Значит тот число в его степени бесконечно приближается к единице. Но то число никогда не станет нулем, и степень ни когда не станет единицей. По этому такой подход не верный. Если использовать логарифму, получается то же самое. Ничего если возвести на степень ни чего, то ничего не будет происходить. Ибо нет какого либо числа, над чем можно работать. Ноль- на самом деле не число а дополнение, без которого математика просто не работает. А само по себе, это ни что. То есть нуля нет.

Любое число в нулевой степени это число деленное на само себя. Поэтому почти всегда это будет 1 так как x/x=1
С нулем немного другая история.
0^0=0/0. А 0/0 не обязательно единица, это неопределенность, ведь на 0 делить нельзя))) это работает для выражения «а в степени b, где a и b стремятся к 0».

Из всего, что нагуглила в интернете, самое доступное для нематематиков обьяснение нашла вот это: «отображение пустого множества в пустое, а оно единственно». Такое литературное выражение хоть как-то (с трудом), но можно переварить.

Математический парадокс,любое число в степени ноль,равно единице,в случае с нолем,ответ считается неочевидным.Просто математический закидон.

Значит так решили принять.
А вообще-то это одна из неопределённостей. Но всё зависит от того, что является этим нулём.

Известно, что абсолютно любое число в нулевой степени равно единице.Если правильно помню,класс 2-3.

Это чисто символически. В нуле эта функция разрывается и не имеет значения

Математики всего мира ещё не пришли к единому мнению по этому вопросу.

Любое число или выражение в нулевой степени равно 1(правило).

Потому что это не так. значение 0 в степени 0 – не определено

Источник

Ноль в нулевой

Предлагаю в таком случае обсудить тот факт, что 0 0 = 1.

*Вылезая из-под стула* Где мой попкорн? Кажется, с прошлого раза ещё должен был остаться

Предел x^x, x->0 есть, но ноль в нулевой — неопределённость.

Вот, что пишет Mathematica:

Однако, вот что она еще пишет:

In[2]:= 0^0
From In[2]:=Power::«indet» : Indeterminate expression 0^0 encountered. More.
Out[2]= Indeterminate

При чём тут предел?

Как это не получим? 0 2 — это ноль, так?

Делим его на ноль, получаем ноль (по определению, ведь найти частное значит найти такое число, которое при умножении на делитель даст делимое; так что ноль нас вполне устраивает: 0×0 = 0). Теперь делим на ноль второй раз, получаем один (снова по определению, так как 1×0 = 0).

Не вижу противоречия.

Опять расписываем, сокращаем. Получаем 1/1=1.

Расписываем аналогично первому. И опять получаем 1/1=1.

Грубо говоря: ноль нолевых ровно 1, так же как одна первая ровно 1.

Ноль нулевых — вот это как раз таки неопределённость. То есть, оно, конечно, равно 1, но оно в той же степени равно и 47. В этом — смысл неопределённости.

А вот 0 0 равно 1, с какой стороны не смотри на него 😉

0/0 и равно 1, и равно 47, безо всякого предела, просто по определению операции деления (найти частное — значит найти такое число, которое при умножении на делитель даст делимое; это и 1, и 47, и даже 920 тысяч). И, поскольку это так, то 0/0 — неопределённость; то есть, существует больше одного значения, которые подпадают под определение этого выражения.

Pardonne moi. Действительно, 0^0 = (47*0)^0 = (47^0)*(0^0) = 1*(0^0) и никаким образом не получить неопределенность (по аналогии с 0/0). Т. е. 0^0 — определенное число. Но чему принять его равным? Самое логичное — равным соответствующему пределу. И всё. Согласен с тобой полностью.

Ну, такую тему я поднять не возьмусь 😉

Кстати, чтобы было веселее, скажу, что 0 0 считал неопределённым не только Фихтенгольц, но и даже более именитые математики.

Илья, это уже провокация 😉

Твои рассуждения неверны. Ты пытаешься разными «махинациями» сделать определённое неопределённым. Иными словами, ты искусственно вводишь в своих преобразованиях неопределённость вида 0/0.

Таким способом можно любое выражение сделать неопределённым. Например, покажем, что 5+5 неопределено, домножив и разделив на ноль («мы же можем домножить и разделить на одно и то же число»):

5+5 = ((5+5)×0)/0 = (10×0)/0 = 0/0 = 47.

Однако это не показывает, что 5+5 неопределено.

Не передёргивай. Лучше ткни конкретно пальцем, где я вношу неопределённость. Нет там такого, неопределённость есть в 0^0 изначально.

Школьное правило математики, которым ты манипулируешь, полностью звучит так «мы можем домножить и разделить на любое одно и то же число, кроме нуля». И за его несоблюдение нам в школе ставили колы без разговоров.

Попробуй найти у меня такую же ошибку 😉

Update (всем): Я уже обнаружил ошибку в данном ответе, но не удаляю его для того, чтобы не сломать последовательность реплик в обсуждении. Ошибка во втором переходе: 0 –5 не равно нулю.

Конечно, ты тщательно замаскировала введение 0/0, но это не значит, что ты его не вводишь. До третьего знака равенства его не было, а после него оно появилось. Вот именно там ты его и вводишь.

5+5 =
= 5+5+0 =
= 5+5+(0 5 ×0 –5 ) =
= 5+5+(0 5 ×1/(0 5 )) =
= 5+5+(0 5 /0 5 ) =
= 5+5+0/0 =
= 5+5+47 =
= 10+47 =
= 57.

Я делаю всё то же, что и ты. Где у меня ошибка? Как только ты найдёшь её у меня, ты найдёшь её и у себя. Либо признай, что 5+5 = 57 😉

Математические выкладки Weasel выглядят убедительнее

Действительно, выкладки Weasel выглядят убедительнее, однако всё равно не являются «математическими», потому, что она занимается — хоть и маскируясь — домножением на неопределённость; не удивительно, что в результате получается неопределённость.

Ниже, кажется, я привёл более удачный пример «неопределённости выражения 5+5».

На самом деле ты уже почти нашёл ошибку 😉

Да, я вот как раз рисовал другую картинку:

Можно бесконечно спорить, используя возведение в целые степени, однако есть определение x^y через две вполне определенные функции: exp() и ln().

обе функции определены для 0 и

Отсюда и 0*ln(0) неопределен.
Кто знает, чему равен lim_x->+0 [ x * ln(x) ]?

Как следствие, 0 0 не определен, Гугл не прав 🙂

Мы оба использовали известные детерминистические методы вычисления x y для доказательства или опровержения 0 0 =1, однако ни один из них не определен для x=0. Следовательно, аргументов против у нас нет 🙂

Интересно, какие же будут аргументы за? Лимиты и выражения «если-то-иначе» — не аргументы ;-).

Я конечно со своим троешным дипломом математика ни на что не претендую, но.

Определение степени ноль скоре всего выводилось как: a^0=a^n*a^-n, а ноль под это определение не попадает!

«Скорее всего» — это не довод. Мне вот естественнее исходить из произведения нуля множителей, которое всегда равно 1.

Делить то, чего нет, очень просто: всем достаётся по «ничего». Или тот факт, что 0/5 = 0 у вас тоже вызывает сомнения?

Только это никакого отношения к вопросу нуля в нулевой не имеет.

В уже упоминавшейся статье после слов «From the power-series point of view, identities such as» идёт формула. Подставьте туда 47 и получите, что e 0 = 47, что неверно.

Кроме того, очевидно, что это не подходит под определение «произведения нуля нулей».

Предложив поменяться ролями, вы признали силу моей точки зрения и предложили мне найти слабость вашей, что, как видим, не составило мне труда.

Дело в том, что в этой формуле изначально полагают, что 0 0 = 1 (Книга Ильина, Позняка). Так что 0 0 все еще может быть равным 47.

Немного поясню. При выводе этой формулы в указаной мною книге делается следующий переход:
1+x/1!+(x^2)/2!+. +(x^n)/n!+. =Сумма от 1 до бесконечности по k (x^(k-1)/(k-1)!). Они говорят, что это верно для любого фиксированного числа х. Т. е. они предполагают (но не доказывают!) что 0 0 =1. Таким образом ничего не мешает мне сказать, что 0 0 =47, а формула верна для любого фиксированного х не равного 0.

Кроме того очевидно, что единица не попадает под определение«произведения нуля нулей».

Как видите у меня еще есть основания считать, что 0 0 =47, и их ровно столько же, сколько у вас считать, что 0 0 =1.

С нетерпением жду поледующих доводов.

П.С. Полностью согласен, что 0,(9)=1 🙂
Там все просто. Там все вытекает из определения.

Ваше высказывание про «очевидно» довольно странное. Мне вот совершенно очевидно, что произведение нуля нулей есть единица. Произведение нуля чего угодно есть единица, и какая разница чего именно, его ведь ноль?

Я пока не увидел на каком основании вы считаете, что 0 0 = 47. Если считать, что это так, то в огромном количестве формул и теорем придётся оговариваться, что «а в случае нуля получится в сорок семь раз меньше».

Мы можем также договориться, что 7 2 = 94, а потом во всех формулах, где используется возведение в степень, указывать, что «в случае 7 2 нужно брать 49, несмотря на то, что это 94». Но не проще ли сразу сказать, что 7 2 = 49, и потом не оговариваться, ведь это так естественно?

Вообще, какое утверждение в математике вы готовы назвать «истинным»?

А теперь перейдем к математическому анализу. Функция непрерывна в точке, если она непрерывна слева и справа от этой точки. (http://www.academiaxxi.ru/WWW_Books/HM/Ma/01/04/t.htm) Надеюсь это вы оспаривать не будете.

А вот теперь вам стоит внимательно почитать определение непрерывности сложной ф-ции. И еще раз прочитать статью (http://www.faqs.org/faqs/sci-math-faq/specialnumbers/0to0/). Там указано, что если взять определеныые функции, и устремить их к нулю слева и справа, то непрерывности в точке 0 не будет. А значит и брать значение функции, как предел в точке 0 нельзя.

А значит и брать значение функции, как предел в точке 0 нельзя.

Я не спорю, что если определить 0^0 как 1, то не придется делать оговорки в огромном количестве формул(а именно по этому в определенных случаях принято слитать 0^0=1), но это не мешает 0^0 равняться 47, и таки делать эти оговорки.

Однако, Google говорит, что Илья прав.

Я-то вам доказал. Если бы это было так, то e 0 было бы равно 47, что неверно.

А вот вы мне не доказали, что 2+2=4, а параллельные прямые не пересекаются.

Где Casio и где Google, нашли что сравнивать! Casio выдаёт ошику, потому, что считает, надо думать, через экспоненту (то есть использует способ выражения существующего через несуществующее).

Дело в том, что в этой формуле изначально полагают, что 0 0 = 1 (Книга Ильина, Позняка). Так что 0 0 все еще может быть равным 47.

Покажите мне хотя бы одну формулу хоть где-нибудь, в которой получался бы правильный результат, если «изначально предполагать», что 0 0 = 47. Как-то так получается, что во всех формулах всё становится хорошо, если изначально предполагать, что 0 0 = 1. Так может правильно предполагают-то, изначально?

Я так и не услышал от вас внятного критерия истины, либо доказательства того, что 2+2=4, а параллельные прямые не пересекаются.

Всё что вы тут трете, либо изъезженные вдоль и поперек факты (Илья Бирман), либо полный бред (Сковородкин).

Поразмышляйте лучше над другой формулой

Тута все 5 констант математических собрано.
===
То, что 2+2=4 можно доказать при определенных условиях, но для этого надо определить что мы подразумеваем под 2, +, = и 4.

По поводу параллельных прямых, которые не пересекаются — написанно криво, параллельность — свойство непересечения прямых, поэтому если прямые пересекаются, то они не параллельны.

Другое дело что существуют геометрии, в которых нельзя через точку вне прямой провести прямую параллельную данной (Риман), либо же их можно провести очень много (Лобачевский).

И зачем я всё это пишу :).

Очень интересными кажутся посты за номерами 11 и 14. Позволю себе тоже внести пять копеек.

Строго говоря, в школьной арифметике мы привыкли останавливать вычисления, если в выражении появляется неопределенность, в частности, вида a\0. Это означает, что при переходе от 0^(a-b) к 0^a*0^(-b) вычисления должны как бы прекращаться, то есть любая учительница здесь говорит: «На ноль делить нельзя».

На первых курсах институтов такие случаи попадаются обычно при рассмотрении функций, и тогда появляется либо предел, либо разрывы какого-нибудь там рода. В чистой арифметике проблема заключается, видимо, в том, что арифметические операции определены только в узких случаях, как например, бесконечные суммы не подчиняются тем же правилам, что и конечные.

Иначе говоря, у Ильи в выражении 0^5*0^(-5) умножение может как-то действовать, но не так, как классическое умножение, не определенное для 0^(-5). На первый взгляд это означает то, что значение (или неопределенность) выражения 0^0 не выводится путем обычных арифметических операций с использованием неопределенностей, поскольку для них арифметика недействительна. Отсюда вывод, что вопрос о том, равно 0^0 единице или нет, для арифметики вообще не важен, поскольку для арифметики он не стоит. Мне кажется, это можно строго доказать.

Анализ я не знаю настолько хорошо, чтобы говорить о задачах, где 0^0=1 удобнее, чем неопределенности. Видимо, это все сведется к доказательству существования предела x^y при x,y->(0,0) и равенства его повторным.

Не понимаю я предмета данного спора.

В математике вводятся новые объекты и правила действия с ними таким образом, чтобы рассуждения с использованием новых объектов давали те же результаты, что и рассуждения только со старыми.

Нулевая и отрицательная степень числа введены для того, чтобы формула a m /a n =a m-n работала не только тогда, когда m>n. Таким образом, по определению, 0 0 есть та же неопределенность, что и 0/0.

Правильным является комментарий номер 11.

По определению чего? Определение в студию.

На комментарий номер 11 я ответил, и позже его автор признала, что в её рассуждениях есть ошибка. Читайте внимательнее.

Переход осуществлялся по биному Ньютона для степени 0

Результат возведения суммы двух чисел в степень 0 равен сумме для i от 0 до 0 произведений количества сочетаний из 0 по i, первого слагаемого, возведенного в степень i и второго слагаемого, возведенного в степень (0-i). Этот ряд вырождается в единственное слагаемое:
(a — a) 0 = C 0 ₀ * a 0 * (-a) 0 = 0! / (0! * (0-0)!) * a 0 * (-1) 0 * a 0 = 1

Ладно. Школьное определение таково: «Нулевая степень любого ненулевого числа есть 1». Но я прекрасно понимаю, какой критике оно может быть подвергнуто. Поэтому предлагаю пока такой аргумент, на уровне матана первого курса 🙂

Таким образом, доопределить функцию по непрерывности нельзя.

Вы, конечно, имеете право утверждать, что 0 0 =1, но я имею точно такое же право утверждать, что 0 0 =0. Поэтому проще сказать, что это неопределенность.

Но это всё ладно. Мне кажется интуитивно понятным, что 0 0 =1, безо всяких пределов и прочей чепухи, и при этом никто из спорящий пока не показал мне никакого противоречия, которое при этом возникало бы.

Какой критике вы можете подвергнуть утверждение о том, что нулевая степень любого числа равна единице? Почему вы исключаете ноль из списка этих чисел? Какие конкретно проблемы возникают у вас с нулём? Каким образом вам удаётся их решить, сказав, что 0 0 неопределено?

Знаете, почему Вам никто не показал противоречия? Просто потому, что до того, как Вы сказали, что 0 0 =1, 0 0 было неопределено. Поэтому 0 0 =1 ничему не противоречит. Но и 0 0 =0 тоже ничему не противоречит.

Вы говорите, что x 0 =1, поэтому 0 0 =1. А я Вам отвечаю: 0 x =0, поэтому 0 0 =0.

А какие проблемы решаете Вы, сказав, что 0 0 =1?

В предпоследнем абзаце вы мне приписываете слова, которых я не говорил.

0 0 противоречит куче формул и теорем. Все эти проблемы исчезают разом, если 0 0 =1. Где-то в обсуждении выше есть ссылка на Википедию, где это подробнее описано. Но, на мой взгляд, намного важнее именно прочувствовать, почему 0 0 =1, потому, что иначе вам будет казаться, что, это значение было искусственно приписано, лишь бы теоремы работали. А на самом деле 0 0 =1 даже безо всяких там теорем 🙂

Я рад за Вас, что Вы это прочувствовали. Наверно, это правильно. Ведь до строгих доказательств математических теорем были наглядные рассуждения. Но математика остается математикой, строгое и формальное доказательство в любом случае необходимо.

Кстати, можете назвать хотя бы несколько теорем и формул, которым «противоречит 0 0 »?

Приведите мне строгое формальное доказательство того, что 2+2=4. На мой взгляд, достаточно того, что это интуитивно понятно, удобно для использования (у вас два яблока и у меня два яблока, если сложить в кучу — будет четыре) и ничему не противоречит. Чтобы что-то формально доказать, нужна какая-то аксиоматическая база, ведь от чего-то надо отталкиваться.

Cтрогое формальное доказательство того, что 2+2=4, можно провести через операцию инкремента (увеличения на 1) 🙂

Я процитировал Ваше «0 0 противоречит куче формул и теорем.» из 42 комментария.

На самом деле всё это несколько надуманные примеры. Уверен, что можно привести примеры, говорящие в пользу того, что 0 0 =0.

Хочу заметить другое. Что такое неопределенность? Если апеллировать к интуиции, то это такое «выражение», которое принимает разные значения в разных ситуациях. Так же есть понятие «раскрытие неопределенности». Например, sin(2x)/x в точке 0 — неопределенность вида 0/0, но вполне естественно считать, что в данном случае это выражение равно 2. Точно так же можно привести пример, где неопределенность 0/0 может быть равна любому числу, или даже бесконечности.

0 0 тоже можно считать неопределенностью, потому что пределы функций x 0 и 0 x в нуле различны.

Мне понятна Ваша позиция, я изложил свою. Полагаю, что на этом наш спор можно прекратить 🙂

Позвольте мне всё же ответить.

Ваш комментарий был бы более убедительным, если бы вы привели хотя бы один пример, говорящий в пользу того, что 0 0 =0, вместо того, чтобы выражать уверенность, что «можно привести такие примеры».

0/0 является неопределённостью по вполне внятному формальному критерию, а не потому, что его «тоже можно считать». А именно. Частным от деления называется такое число, умножение которого на делитель даст делимое. Под это определение подпадает и 47 (0×47=0), и 1024 (0×1024=0). Вот поэтому — неопределённость. Это первый этап — признание неопределённости исходя из определения. Далее делается попытка доопределить. Например, будем считать, что 0/0=1, так как x/x=1, и вроде бы удобно доопределить с помощью непрерывности. Однако быстро выясняется, что если принять 0/0=1, то можно доказать, что 2=3, то есть это нас приводит к противоречию. Противоречие может следовать только из ложного высказывание, значит 0/0=1 — ложь. Это второй этап — признание невозможности искусственно «удобно» доопределить.

Можно привести пример, где неопределённость вида 0/0 может быть равна любому числу, это не вызывает сомнения. Вы приведите пример, когда «неопределённость» вида 0 0 может быть равна числу иному, чем 1. Вы говорите: «Вот, есть же неопределённости, они ведь бывают? Вот значит это тоже неопределённость».

По крайней мере одна из функций x 0 и 0 x обязана иметь разрыв в точке ноль, это мы уже обсудили. Вы предлагаете для какого-то непонятного равновесия сделать так, чтобы разрыв был у обеих. Кому это нужно и зачем — загадка.

Источник