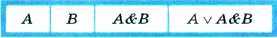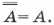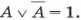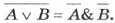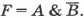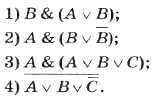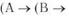Неверно что в логике знак
Неверно что в логике знак
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
СИМВОЛИКА ЛОГИЧЕСКАЯ
– система знаков (символов), используемая в логике для обозначения термов, предикатов, высказываний, логических функций, отношений между высказываниями. В разных логических системах могут использоваться различные системы обозначений, поэтому ниже мы приводим лишь наиболее употребительные символы из числа используемых в литературе по логике:
– начальные буквы латинского алфавита, обычно используются для обозначения индивидуальных константных выражений, термов;
– прописные начальные буквы латинского алфавита, обычно используются для обозначения конкретных высказываний;
– буквы, стоящие в конце латинского алфавита, обычно используются для обозначения индивидных переменных;
– знаки, служащие для обозначения отрицания; читаются: «не», «неверно что»;
– знаки для обозначения конъюнкции – логической связки и высказывания, содержащего такую связку в качестве главного знака; читаются: «и»;
– знак для обозначения неисключающей дизъюнкции – логической связки и высказывания, содержащего такую связку в качестве главного знака; читается: «или»;
– знак для обозначения строгой, или исключающей, дизъюнкции; читается: «либо, либо»;
– знаки для обозначения импликации – логической связки и высказывания, содержащего такую связку в качестве главного знака; читаются: «если, то»;
– знаки для обозначения эквивалентности высказываний; читаются: «если и только если»;
– знак, обозначающий выводимость одного высказывания из другого, из множества высказываний; читается: «выводимо» (если высказывание А выводимо из пустого множества посылок, что записывается как « A», то знак « » читается: «доказуемо»);
– истина (от англ. true – истина); – ложь (от англ. false – ложь);
– квантор общности; читается «для всякого», «всем»;
– квантор существования; читается: «существует», «имеется по крайней мере один»;
– знаки для обозначения модального оператора необходимости; читаются: «необходимо, что»;
– знаки для обозначения модального оператора возможности; читаются: «возможно, что».
Наряду с перечисленными в многозначных, временных, деонтических и других системах логики используются свои специфические символы, однако каждый раз разъясняется, что именно тот или иной символ обозначает и как он читается (см.: Знак логический).
Поделиться ссылкой на выделенное
Нажмите правой клавишей мыши и выберите «Копировать ссылку»
Алгебра логики знаки и их обозначения
Обозначения в логических операциях
Обозначения для логических связок:
отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);
конъюнкция (логическое умножение, логическое И) обозначается /
дизъюнкция (логическое сложение, логическое ИЛИ) обозначается /
следование (импликация) обозначается → (например, А → В);
тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);
символ 1 (единица) используется для обозначения истины (истинного высказывания);
символ 0 (ноль) используется для обозначения лжи (ложного высказывания).
Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) / В равносильны, а А / В и А / В – нет (значения выражений разные, например, при А = 1, В = 0).
Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А / В / С / D означает то же, что и
Возможна запись А / В / С вместо (А / В) / С. То же относится и к конъюнкции: возможна запись А / В / С вместо (А / В) / С.
Свойства логических операций
Общие свойства логических операций
Для набора из n логических переменных существует ровно 2n различных значений. Таблица истинности для логического выражения от n переменных содержит n+1 столбец и 2n строк.
Дизъюнкция
Если хоть одно из подвыражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.
Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже истинна.
Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.
Значение дизъюнкции не зависит от порядка записи подвыражений, к которым она применяется.
Конъюнкция
Если хоть одно из подвыражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.
Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.
Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то конъюнкция этих выражений тоже ложна.
Значение конъюнкции не зависит от порядка записи подвыражений, к которым она применяется.
Простые дизъюнкции и конъюнкции
Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.
Простая конъюнкция принимает значение 1 (истина) ровно на одном наборе значений переменных.
Простая дизъюнкция принимает значение (ложь) ровно на одном наборе значений переменных.
Импликация
Импликация A →B равносильна дизъюнкции (¬А) / В. Эту дизъюнкцию можно записать и так: ¬А / В.
Импликация A →B принимает значение 0 (ложь) только если A=1 и B=0. Если A=0, то импликация A →B истинна при любом значении B.
Ключевые слова:
1.3.1. Высказывание

Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.

Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six Is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.

Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.
Относительно предложения «Компьютерная графика — самая интересная тема в курсе школьной информатики» также нельзя однозначно сказать, истинно оно или ложно. Подумайте сами почему.

Например, не являются высказываниями такие предложения, как: «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл?».

Примерами высказываний могут служить:
Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:
Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «X n — 1;
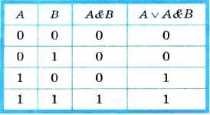
Построим таблицу истинности для логического выражения A ∨ А & В. В нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:
Наборы входных переменных — это целые числа от О до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11. Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение A ∨ А & Б равносильно логическому выражению А.
1.3.4. Свойства логических операций
Рассмотрим основные свойства (законы) алгебры логики.
- Переместительный (коммутативный) закон
- для логического умножения:
для логического сложения:
Сочетательный (ассоциативный) закон
- для логического умножения:
для логического сложения:
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
Распределительный (дистрибутивный) закон
- для логического умножения:
для логического сложения:
A ∨ (B & С) = (A ∨ В) & (A ∨ С).
Двойное отрицание исключает отрицание.
Закон исключения третьего
- для логического умножения:
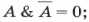
для логического сложения:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
Закон повторения
- для логического умножения:
для логического сложения:
Законы операций с 0 и 1
- для логического умножения:
для логического сложения:
Законы общей инверсии
- для логического умножения:
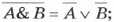
для логического сложения:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности.
Докажем распределительный закон для логическического сложения:
A ∨ (В & С) = (А ∨ В) & (A ∨ С).
Совпадение столбцов, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Пример 2. Найдём значение логического выражения 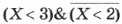
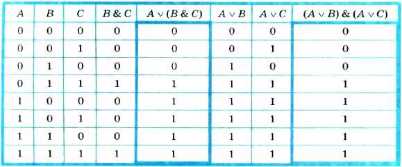
1 С учётом того, что ваза разбита одним внуком, можно было составлять не всю таблицу, а только её фрагмент, содержащий следуюнще наборы входных переменных: 001, 010, 100.
Исходя из того, что знает о внуках бабушка, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10). Таких строк в таблице оказалось две (они отмечены галочками). Согласно второй из них, вазу разбили Коля и Вася, что противоречит условию. Согласно первой из найденных строк, вазу разбил Серёжа, он же оказался хитрецом. Шутником оказался Вася. Имя правдивого внука — Коля.
Задача 2. В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах?
Решение. Рассмотрим простые высказывания:
C1 = «Сима заняла первое место»;
В2 = «Валя заняла второе место»;
С2 = «Сима заняла второе место»;
Д3 = «Даша заняла третье место»;
А2 = «Алла заняла второе место»;
Д4 = «Даша заняла четвёртое место».
Так как в каждом из трёх предположений одно из высказываний истинно, а другое ложно, то можно заключить следующее:
Логическое произведение истинных высказываний будет истинным:
На основании распределительного закона преобразуем левую часть этого выражения:
Высказывание С1 • С2 означает, что Сима заняла и первое, и второе места. Согласно условию задачи, это высказывание ложно. Ложным является и высказывание В2 • С2. Учитывая закон операций с константой 0, запишем:
Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных высказываний дают:
Из последнего равенства следует, что С1 = 1, Д3 = 1, А2 = 1. Это означает, что Сима заняла первое место, Алла — второе, Даша — третье. Следовательно, Валя заняла четвёртое место.
Познакомиться с другими способами решения логических задач, а также принять участие в Интернет-олимпиадах и конкурсах по их решению вы сможете на сайте «Математика для школьников» (http://www.kenqyry.com/).
На сайте http://www.kaser.com/ вы сможете скачать демонстрационную версию очень полезной, развивающей логику и умение рассуждать логической головоломки Шерлок.
1.3.6. Логические элементы
Алгебра логики — раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Вы уже знаете, что любая информация может быть представлена в дискретной форме — в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
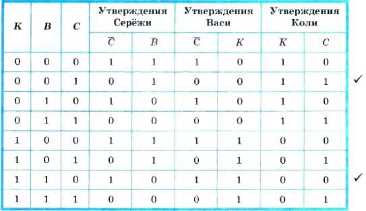
На рис. 1.5 приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.
Рис 1.5.
Логические элементы
Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 1.5, а). Единица на выходе этого элемента появится только тогда, когда на всех входах будут единицы.
Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рис. 1.5, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.
Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 1.5, в). Если на входе элемента О, то на выходе 1 и наоборот.
Компьютерные устройства, производящие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти вопросы будут раскрыты в курсе информатики 10-11 классов.
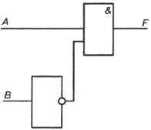
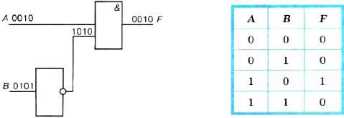
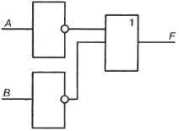
Пример 3. Проанализируем электронную схему, т. е. выясним, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах.
Решение. Все возможные комбинации сигналов на входах А к В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.
Таблицу истинности можно построить и по логическому выражению, соответствующему электронной схеме. Последний логический элемент в рассматриваемой схеме — конъюнктор. В него поступают сигналы от входа Л и от инвертора. В свою очередь, в инвертор поступает сигнал от входа В. Таким образом,
Составить более полное представление о логических элементах и электронных схемах вам поможет работа с тренажёром «Логика» (http://kpolyakov. narod. ru/prog/logic. htm).
Самое главное
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
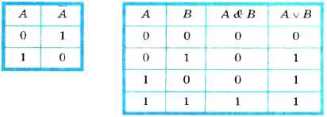
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.
Таблицы истинности для основных логических операций:
При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций:
Вопросы и задания
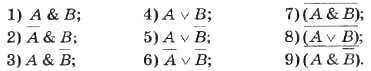
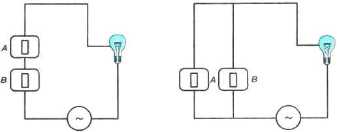
Рассмотрите представленные на рисунке электрические схемы:
На них изображены известные вам из курса физики параллельное и последовательное соединения переключателей. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателей. Попытайтесь самостоятельно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:

Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:
По запросу сомики & гуппи было найдено 0 сайтов, по запросу сомики & меченосцы — 20 сайтов, а по запросу меченосцы & гуппи — 10 сайтов.
Сколько сайтов будет найдено по запросу сомики | меченосцы | гуппи?
Для скольких сайтов рассматриваемого сегмента ложно высказывание «Сомики — ключевое слово сайта ИЛИ меченосцы — ключевое слово сайта ИЛИ гуппи — ключевое слово сайта»?
Постройте таблицы истинности для следующих логических выражений:
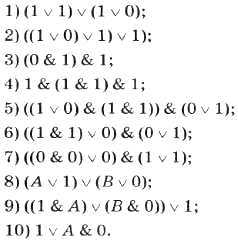
Найдите значение логического выражения 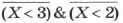
Пусть А = «Первая буква имени — гласная», В = «Четвёртая буква имени согласная». Найдите значение логического выражения 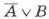
Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:
Смит: «Я не делал этого. Браун сделал это».
Джон: «Браун не виновен. Смит сделал это».
Браун: «Я не делал этого. Джон не делал этого».
Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду. Кто из подозреваемых должен быть оправдан?
Электронное приложение к уроку
 |  |  |
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
Специально созданный для целей логики язык получил название формализованного. Слова обычного языка заменяются в нем отдельными буквами и различными специальными символами. Формализованный язык — это «насквозь символический» язык, в котором нет ни одного слова обычного языка. В формализованном языке содержательные выражения заменяются буквами, а в качестве логических символов (логических постоянных) используются символы со строго определенным значением.
В логической литературе используются различные системы обозначений, поэтому ниже даются два и более вариантов символов.
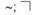
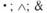
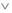

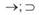
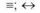
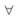
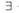
L, N, — знаки для обозначения модального оператора необходимости; читаются: «необходимо, что»;
М — знак для обозначения модального оператора возможности; читается: «возможно, что».
Наряду с перечисленными, в многообразных системах логики используются и другие специфические символы, при этом каждый раз разъясняется, что именно тот или иной символ обозначает и как он читается.
В качестве знаков препинания в искусственных языках логики используются, как и в языке математики, скобки.
А) «Тот, кто ясно мыслит, ясно говорит» — 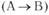
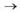
Б) «Он — образованный человек и неправда, что он не знаком с сонетами Шекспира» — 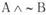
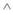
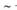
В) «Если свет имеет волновую природу, то, когда он представляется в виде потока частиц (корпускул), допускается ошибка» — 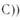
Г) «Если вы были в Париже, то вы видели Лувр или видели Эйфелеву башню» — 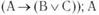
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10605 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно