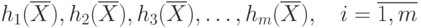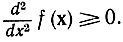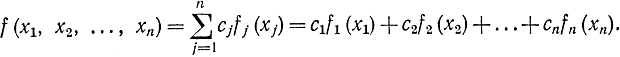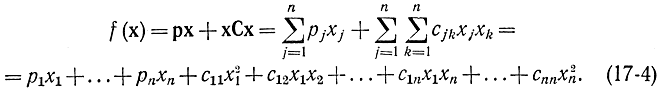Неверно что программирование относится к нелинейному программированию
Лекция 7: Нелинейное программирование. Классификация методов нелинейного программирования. Классический метод определения условного экстремума. Метод множителей Лагранжа
1. Понятие нелинейного программирования
Пусть в математической модели проектируемого объекта или процесса непрерывная функция 
Тогда задача нелинейного программирования может быть сформулирована следующим образом:
найти вектор 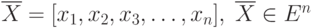

В течение последних двух десятилетий из нелинейного программирования выделились самостоятельные разделы:
Задачи выпуклого программирования – это задачи, в которых определяется минимум выпуклой функции (или максимум вогнутой), заданной на выпуклом замкнутом множестве. Эти задачи среди задач нелинейного программирования наиболее изучены.
Среди задач выпуклого программирования более подробно изучены задачи квадратичного программирования. В этих задачах целевая функция – квадратична, а ограничения – линейны.
В задачах целочисленного программирования неизвестные параметры могут принимать только целочисленные значения.
В задачах стохастического программирования в целевой функции или в функциях ограничений содержатся случайные величины, которые подчиняются законам теории вероятностей.
В задачах динамического программирования ограничения содержат как параметр время и при этом описываются дифференциальными уравнениями. Процесс нахождения решений в задачах динамического программирования является многоэтапным.
Неверно что программирование относится к нелинейному программированию
Глава семнадцатая. Нелинейное программирование
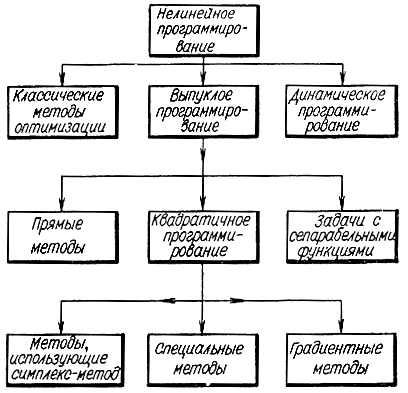
17-1. Классификация методов нелинейного программирования
Нелинейное программирование включает в себя методы определения минимума функции n переменных F(х), где х = || x1, x2, x3 || при m + n ограничивающих условиях
Соотношения (17-2) следует понимать таким образом, что каждая компонента векторов ψ и x них не менее нуля. Иногда сокращенно соотношения (17-1) и (17-2) записывают в виде
где область G задается условиями
В нелинейном программировании допускаются в общем случае любые соотношения между n и m, т. е. n>m, n = m, m 1 +(1-λ)x 2 >≤λf(x 1 )+(1-λ)f(x 2 ) (17-3)
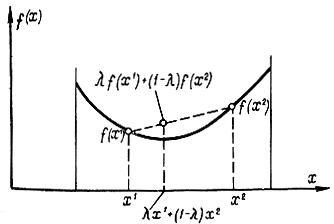
где 0 1 ) и f(х 2 ). На рис. 17-2 приведен пример выпуклой функции одной переменной.
Рис. 17-1. Классификация методов нелинейного программирования
Следует заметить, что определение вогнутости и выпуклости может показаться на первый взгляд неправильным. Например, тарелка, стоящая на столе, считается вогнутой, но если рассматривать ее с точки зрения нашего определения, т. е. при направлении третьей оси вверх, она выпукла. Дело в том, что обычное понятие выпуклости всегда совпадает с математическим, если смотреть по положительному, а не по отрицательному направлению оси, относительно которой определяется выпуклость. В примере с тарелкой на столе на нее следует смотреть снизу, стола, тогда она будет выпуклой. Заметим, что для выпуклых функций (см. рис. 17-2)
Рис. 17-2. К определению выпуклой функции
В общем случае эти функции не являются выпуклыми. Однако если каждая из функций fj(xj) выпуклая и коэффициенты cj неотрицательны, то функция f(х) тоже выпуклая. Методы решения задач с сепарабельными функциями, основанные на замене нелинейных функций ломаными кривыми, составленными из отрезков прямых, ищут локальный экстремум и не гарантируют отыскание глобального экстремума [Л. 89].
Теоретически наиболее широко и детально в нелинейном программировании разработан раздел выпуклого программирования, называемый Квадратичным, в котором функции представляются в виде суммы линейной и квадратичной форм и имеют вид:
Для выпуклости необходимо, чтобы матрица C = [| cjk || представляла собой симметричную положительную полуопределенную матрицу, т. е. чтобы для любых x выполнялись условия симметрии cjk = ckj и положительной полуопределенности хСх≥0.
Однако и этот достаточно узкий раздел не представляет единого целого, а состоит из набора методов, справедливых для более частных видов функции (17-5) и отличающихся разной эффективностью, для которой пока еще нет удобных способов сравнительной оценки.
Методы квадратичного программирования можно разделить на три группы: алгоритмы, использующие симплекс-метод; градиентные и прочие специальные методы (см. рис. 17-1).
Отличие градиентные методов, рассматриваемых в квадратичном программировании, от рассмотренных в разделе прямых методов заключается в том, что в первом случае благодаря заданию функций в виде (17-4) удается получить значительно больше результатов, характеризующих конкретный метод. В прямых методах поиска в градиентных и других алгоритмах, как правило, функция цели неизвестна (считается просто, что она выпукла), в традиционных руководствах по нелинейному программированию в большинстве случаев она задана аналитически, в виде таблиц или другим способом. Прямые методы по традиции много внимания уделяют аспектам поиска «вслепую» в условиях неопределенности, выбору оптимальной в каждом случае стратегии поиска.
Нелинейное программирование
1. Постановка задачи
2. Метод множителей Лагранжа
3. Теорема Куна-Таккера. Условие регулярности Слейтера
4. Выпуклое и вогнутое программирование
5. Квадратичное программирование
6.1 Постановка задачи
Задача нелинейного программирования в общем случае формулируется следующим образом:
при условиях
Задача нелинейного программирования называется также задачей на условный экстремум.
В отличие от задач линейного программирования для задач нелинейного программирования не существует универсального метода решения.
В задачах линейного программирования область допустимых решений R(x) всегда является выпуклым с конечным числом крайних точек. Перебрав только крайние точки, всегда за конечное число шагов можно найти оптимальное решение. В задачах нелинейного программирования нелинейность ограничений не всегда обеспечивает выпуклость области допустимых решений и конечность числа его крайних точек. Из-за этих особенностей и возникают основные трудности решения задач нелинейного программирования.
Пример 1. Область допустимых решений R(x) определена ограничениями:
Область допустимых решений имеет вид (Рисунок 6.1) и является не выпуклой.
Пример 2. Область допустимых решений R(x) определена ограничениями:
Область допустимых решений имеет вид (Рисунок 6.2), является выпуклой, но имеет бесконечное число крайних точек.
6.2 Метод множителей Лагранжа
Для того, чтобы вектор 


Таким образом, метод множителей Лагранжа состоит из следующих шагов:
1. Составляем функцию Лагранжа L(X, L).
2. Составляем систему уравнений.
3. Находим ее решение 
6.2.1 Исследование функции на экстремум
Для того, чтобы стационарная точка Х0 была экстремальной, достаточно чтобы матрица Гессе H в точке Х0 была:
Ø положительно определенной, тогда Х0 – точка min;
Ø отрицательно определенной, тогда Х0 – точка max.
Для двумерной функции f(x1, x2) матрица Гессе имеет вид
Для трехмерной функции f(x1, x2, x3) матрица Гессе имеет вид
Квадратичная форма Q(X) является положительно определенной, если значения всех угловых миноров определителя ½А½ положительны. В этом случае матрица А называется положительно определенной.
k-м угловым минором определителя матрицы A(n´n) называется определитель вида
Пример. Пусть точка 

Пусть матрица Гессе имеет вид

Определим k-е угловые миноры:
Так как матрица Гессе является отрицательно определенной, то точка 
6.3 Теорема Куна-Таккера. Условие регулярности Слейтера
Условие оптимальности решения задачи нелинейного программирования формулируется в теореме Куна-Таккера, имеющей важное значение для теории нелинейного программирования.
Определим функцию Лагранжа следующим образом
Тогда теорему Куна-Таккера можно записать:
6.4 Выпуклое и вогнутое программирование
Частным случаем задачи нелинейного программирования является задача выпуклого программирования, которая формулируется следующим образом: найти min<f(X)> при условиях
Применив теорему Куна-Таккера, получим следующие необходимые и достаточные условия оптимальности: если функции f(X), gi(X) дифференцируемы и выпуклы по Х, то вектор Х0 является оптимальным решением задачи выпуклого программирования тогда и только тогда, когда существует такой вектор 

Задачу выпуклого программирования решают следующим образом:
1. Составляют функцию Лагранжа
2. Записывают условие оптимальности в виде системы уравнений и неравенств.
3. Находят совместное решение 
Задача вогнутого программирования формулируется следующим образом: найти max<f(X)> при условиях
Покажем эквивалентность данной задачи задаче выпуклого программирования. Введем обозначения f*(X) = – f(X) и g*i(X) = – gi(X). Так как max< f(X)> = min<– f(X)>, то приходим к задаче:
Условия оптимальности формулируются аналогично задаче выпуклого программирования: Пусть функции f(X), gi(X) дифференцируемы и вогнуты по Х. Для того, чтобы вектор Х0 являлся оптимальным решением задачи вогнутого программирования необходимо существование такого вектора 

Таким образом, для решения задачи вогнутого программирования необходимо найти совместное решение 
6.5 Квадратичное программирование
Задачи квадратичного программирования представляют собой специальный класс задач нелинейного программирования, для которых целевая функция квадратичная, а все ограничения линейные.
Эта задача формулируется следующим образом:
найти max(min)< f(X)>= BтX + XтCX = 

где 
Матрица С будет отрицательно определенной в задаче максимизации и положительно определенной в задаче минимизации. Это означает, что функция f(X) является выпуклой по переменным Х в задаче минимизации и вогнутой в задаче максимизации. Ограничения в этой задаче предполагаются линейными, что гарантирует выпуклость области допустимых решений.
Применив теорему Куна-Таккера, получим следующие необходимые и достаточные условия оптимальности: вектор 



Первые два условия образуют систему из (n + m) линейных уравнений с 2(n + m) неизвестными (векторы X0, L0, V0, W0). Третье и четвертое – это условие дополняющей нежесткости, которые налагают дополнительные ограничения на переменные X0, L0, V0, W0, а именно:
В силу этих условий искомое решение задачи должно быть одним из допустимых базисных решений. Для его отыскания можно применить любой из методов линейного программирования, например, симплекс-метод.
Математическое программирование. Линейное и нелинейное программирование
Характеристика математического программирования как отдельной дисциплины. Понятие линейного, нелинейного и динамического программирования. Методы решения задач: графический, симплексный методы; постановка двойственной задачи; метод множителей Лагранжа.
| Рубрика | Математика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 15.08.2014 |
| Размер файла | 71,5 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Размещено на http://www.allbest.ru/
Линейное и нелинейное программирование
1. Понятие математического программирования
2. Понятие линейного программирования. Виды задач линейного программирования
3. Понятие нелинейного программирования
4. Динамическое программирование
Пример (задача линейного программирования)
Известно, что определенный вид продукции можно произвести, используя различные технологические способы; в некоторых производствах возможна взаимозаменяемость материалов; один и тот же тип оборудования может быть использован для производства различных видов продукции и т.п.
Как лучше организовать производство, по каким ценам выгодно производить продукцию, как лучше всего использовать производственные ресурсы, которые высвобождаются и т.п.?
На все эти вопросы позволяет получить ответ математическое программирование, являющееся действенным инструментом принятия решений.
Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения.
В зависимости от свойств функций f и gi математическое программирование можно рассматривать как ряд самостоятельных дисциплин, занимающихся изучением и разработкой методов решения определенных классов задач.
Прежде всего задачи математического программирования делятся на задачи линейного и нелинейного программирования. При этом если все функции f и gi линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования. Наиболее изученным разделом математического программирования является линейное программирование. Для решения задач линейного программирования разработан целый ряд эффективных методов, алгоритмов и программ. Среди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования. Это задачи, в результате решения которых определяется минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
В свою очередь, среди задач выпуклого программирования более подробно исследованы задачи квадратичного программирования. В результате решения таких задач требуется в общем случае найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных неравенств или линейных уравнений либо некоторой системе, содержащей как линейные неравенства, так и линейные уравнения.
В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения.
Задача, процесс нахождения решения которой является многоэтапным, относится к задаче динамического программирования.
математический программирование динамический лагранж
1. Понятие математического программирования
Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.
Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ.
Математическое программирование можно рассматривать как совокупность самостоятельных разделов, занимающихся изучением и разработкой методов решения определенных классов задач.
В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса:
· задачи линейного программирования,
· задачи нелинейного программирования;
· задачи динамического программирования.
2. Понятие линейного программирования. Виды задач линейного программирования
Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности.
Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного представления реального мира.
Линейное программирование применяется при решении экономических задач, в таких задачах как управление и планирование производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определения оптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д.
Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.
Существует несколько методов решения задач ЛП:
Ш Графический метод решения задачи ЛП;
Ш Симплексный метод;
Ш Решение задачи ЛП средствами табличного процессора Excel;
3. Понятие нелинейного программирования
В большинстве инженерных задач построение математической модели не удается свести к задаче линейного программирования.
В данной работе будет рассматриваться такой метод решения задач НП, как метод множителей Лагранжа.
Метод множителей Лагранжа позволяет отыскивать максимум (или минимум) функции при ограничениях-равенствах. Основная идея метода состоит в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой построенной функции Лагранжа.
4. Динамическое программирование
Динамическое программирование представляет собой математические аппарат, позволяющий быстро находить оптимальное решение в случаях, когда анализируемая ситуация не содержит факторов неопределенности, но имеется большое количество вариантов поведения, приносящих различные результаты, среди которых необходимо выбрать наилучший. Динамическое программирование подходит к решению некоторого класса задач путем разложения на части, небольшие и менее сложные задачи. В принципе, задачи такого рода могут быть решены путем перебора всех возможных вариантов и выбора среди них наилучшего, однако часто такой перебор весьма затруднен. В этих случаях процесс принятия оптимального решения может быть разбит на шаги (этапы) и исследован с помощью метода динамического программирования.
Решение задач методами динамического программирования проводится на основе сформулированного Р.Э.Беллманом принципа оптимальности: оптимальное поведение обладает тем свойством, что каким бы ни было первоначальное состояние системы и первоначальное решение, последующее решение должно определять оптимальное поведение относительно состояния, полученного в результате первоначального решения.
Таким образом, планирование каждого шага должно проводится с учетом общей выгоды, получаемой по завершении всего процесса, что и позволяет оптимизировать конечный результат по выбранному критерию.
Вместе с тем динамическое программирование не является универсальным методом решения. Практически каждая задача, решаемая этим методом, характеризуется своими особенностями и требует проведения поиска наиболее приемлемой совокупности методов для ее решения. Кроме того, большие объемы и трудоемкость решения многошаговых задач, имеющих множество состояний, приводят к необходимости отбора задач малой размерности либо использования сжатой информации.
Динамическое программирование применяется для решения таких задач, как: распределение дефицитных капитальных вложений между новыми направлениями их использования; разработка правил управления спросом и запасами; составление календарных планов текущего и капитального ремонтов оборудования и его замены; поиск кратчайших расстояний на транспортной сети и т.д.
Все решения задачи разбиваются на два этапа. На первом этапе, который называют условной оптимизацией, отыскиваются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего.
После того, как функция Беллмана и соответствующие оптимальные управления найдены для всех шагов с n-го по первый, производится второй этап решения задачи, который называется безусловной оптимизацией.
В общем виде задача динамического программирования формулируется следующим образом: требуется определить такое управление X*, переводящее систему из начального состояния S0 в конечное состояние Sn, при котором целевая функция F(S0,X*) принимает наибольшее (наименьшее) значение.
Особенности математической модели динамического программирования заключаются в следующем:
задача оптимизации формулируется как конечный многошаговый процесс управления;
целевая функция является аддитивной и равна сумме целевых функций каждого шага
выбор управления Xk на каждом шаге зависит только от состояния системы к этому шагу Sk-1 и не влияет на предшествующие шаги (нет обратной связи);
состояние системы Sk после каждого шага управления зависит только от предшествующего состояния системы Sk-1 и этого управляющего воздействия Xk (отсутствие последействия) и может быть записано в виде уравнения состояния:
на каждом шаге управление Xk зависит от конечного числа управляющих переменных, а состояние системы Sk зависит от конечного числа переменных;
оптимальное управление X* представляет собой вектор, определяемый последовательностью оптимальных пошаговых управлений:
число которых и определяет количество шагов задачи.
Условная оптимизация. Как уже отмечалось выше, на данном этапе отыскиваются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего в соответствии с алгоритмом обратной прогонки. На последнем n-м шаге найти оптимальное управление X*n и значение функции Беллмана Fn(S) не сложно, так как
где максимум ищется по всем возможным значениям Xn.
Дальнейшие вычисления производятся согласно рекуррентному соотношению, связывающему функцию Беллмана на каждом шаге с этой же функцией, но вычисленной на предыдущем шаге:
Этот максимум (или минимум) определяется по всем возможным для k и S значениям переменной управления X.
Безусловная оптимизация. После того, как функция Беллмана и соответствующие оптимальные управления найдены для всех шагов с n-го по первый (на первом шаге k=1 состояние системы равно ее начальному состоянию S0), осуществляется второй этап решения задачи. Находится оптимальное управление на первом шаге X1, применение которого приведет систему в состояние S1(S,x1*), зная которое можно, пользуясь результатами условной оптимизации, найти оптимальное управление на втором шаге, и так далее до последнего n-го шага.
Для заданной математической постановки задачи ЛП, приняв дополнительно условие неотрицательности переменных, выполнить следующие действия:
Решить задачу графическим методом;
Привести задачу к канонической форме записи;
Составить симплексную таблицу;
Произвести решение задачи симплексным методом ручным способом или с использование компьютера;
Осуществить постановку двойственной задачи ЛП;
Получить решение двойственной задачи из полученной ранее симплексной таблицы и произвести анализ полученных результатов;
Проверить результаты решения в табличном процессоре Excel;
Составить отчет с приведение результатов по каждому пункту.