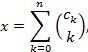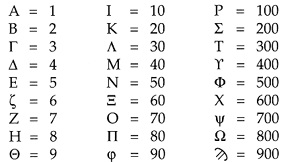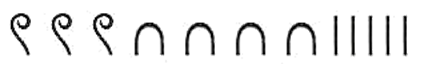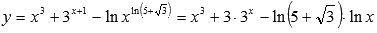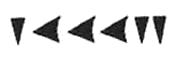Непозиционная система счисления что это
Какие системы счисления называются непозиционными
Что таоке непозиционная система счисления в информатике
В информатике используют позиционный и непозиционный метод записи чисел. Позиционный способ предполагает представление числовых обозначений в определенной последовательности для сохранения величины числа.
Непозиционная система счисления – это способ записи числа с помощью символов, в котором изменение положения знаков не влияет на значение величины числа.
Разновидности непозиционных систем счисления с примерами
Существует несколько видов непозиционной системы исчисления.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Биномиальная
В данном методе для записи чисел применяются биноминальные коэффициенты.
Биноминальные коэффициенты – это объединение количества сочетаний, определенное лишь для неотрицательных целых чисел. Такие обобщения зачастую возникают в задачах, требующих перебора всех возможных вариантов ответов, а также в теории вероятности.
Число x в рассматриваемой системе представляет собой сумму биноминальных коэффициентов:
Биноминальные числа бывают:
Пример преобразования матричной формы в линейную:
Каждой составляющей матрицы соответствует один биноминальный коэффициент. При сложении коэффициентов, соответствующих единицам в матрице, получится количественный эквивалент.
Применение биноминальных чисел:
Греческая
Греческая система счисления – это метод представления числа с помощью букв греческого алфавита и некоторых знаков доклассического периода. Другие названия данного способа – ионийская, новогреческая.
В Греции рассматриваемый алфавитный способ записи чисел стал применяться в III веке до н.э. Буквы греческого алфавита соответствуют следующим числам:
С помощью ионийской системы можно записать лишь числа от 1 до 999.
Римская
Римская система исчисления – это метод числовой записи посредством использования символов латинского алфавита.
Соответствие букв латиницы числовому значению:
Для представления чисел десятичной системы счисления в виде римских букв работают следующие правила:
При переводе числа 67 в римскую систему счисления получаем следующий набор латинских букв: LXVII = (50 + 10) + (5 + 2) = 60 + 7.
Применение данной системы исчисления:
Древнеегипетская
Способ записи чисел, используемый в Древнем Египте, основывался на иероглифах. С помощью этих символов записывались основные числа 1, 10, 100 и т.д. Другие числовые значения получались с помощью сложения ключевых чисел.
Действие производилось в следующей последовательности:
Вавилонская
Вавилонская система исчисления – это позиционный метод записи чисел с основанием 60, применявшийся в Древнем Вавилоне. Это первая известная шестидесятеричная система.
В данной системе счисления числа записываются справа налево в порядке убывания: сотни, десятки, единицы. Досчитав до 60, отмечают новый числовой ряд, запись чисел вновь начинается с 1.
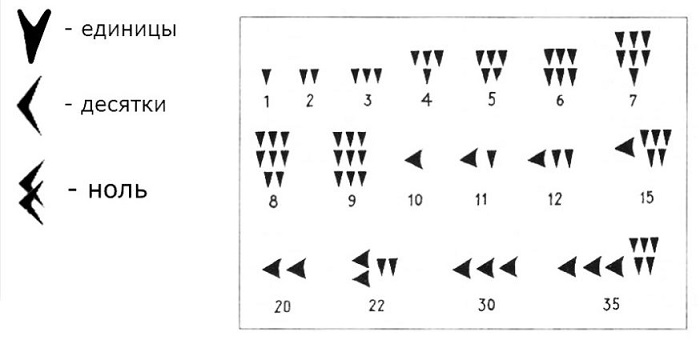
Цифрами вавилонского числового метода считались клинья, разные для записи единиц, десятков и нуля.
В измерении времени: час состоит из 60 минут, а минуты – из 60 секунд.
В измерении углов: градус равен 60 минутам, а минута – 60 секундам.
Система счисления майя
Цифры майя – это позиционная запись чисел с основанием 20, используемая племенами майя.
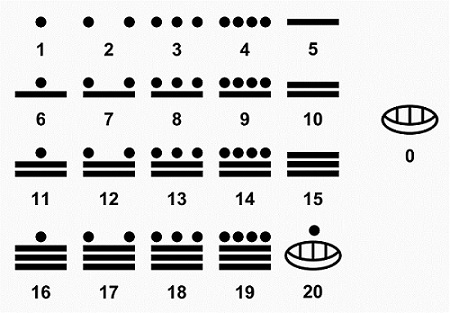
Рассматриваемый способ исчисления состоял из нуля и 19 сложных цифр. Ноль имел обозначение пустой ракушки. Цифры составлялись из точки и горизонтальной черточки. Точка означала единицу, черта – пятерку.
Цифры майя применялась в календарных расчетах. В бытовых целях использовали непозиционный метод записи. Об этом свидетельствует то, что в позиционной системе счисления цивилизации майя имеется больше чисел, чем необходимые 12.
Системы счисления
Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).
Системы счисления бывают:
Непозиционные системы счисления
Примеры: унарная, римская, древнерусская и др.
Позиционные системы счисления
Основание системы счисления —
количество различных цифр, используемых в этой системе.
отношение количественного эквивалента цифры в этом разряде к количественному эквиваленту той же цифры в нулевом разряде
где i — номер разряда, а s — основание системы счисления.
Разряды числа нумеруются справа налево, причем младший разряд целой части (стоящий перед разделителем — запятой или точкой) имеет номер ноль. Разряды дробной части имеют отрицательные номера:
По определению веса разряда
где i — номер разряда, а s — основание системы счисления.
Тогда, обозначив цифры числа как ai, любое число, записанное в позиционной системе счисления, можем представить в виде:
Например, для системы счисления с основанием 4:
Выполнив вычисления, мы получим значение исходного числа, записанное в десятичной системе счисления (точнее, в той, в которой производим вычисления). В данном случае:
= 1⋅64 + 3⋅16 + 0⋅4 + 2⋅1 + 2⋅0,25 =
= 64 + 48 + 2 + 0,5 = 114,5
Таким образом, для перевода числа из любой системы счисления в десятичную следует:
Вспомним пример перевода из системы счисления с основанием 4 в десятичную:
13024 = 1⋅4 3 + 3⋅4 2 + 0⋅4 1 + 2⋅4 0 = 114
Иначе это можно записать так:
114 = ((1 ⋅ 4 + 3) ⋅ 4 + 0) ⋅ 4 + 2 = 13024
Отсюда видно, что при делении 114 на 4 нацело в остатке должно остаться 2 — это младшая цифра при записи в четверичной системе. Частное же будет равно
Деление его на 4 даст остаток — следующую цифру (0) и частное 1 ⋅ 4 + 3. Продолжая действия, получим аналогичным образом и оставшиеся цифры.
В общем случае для перевода целой части числа из десятичной системы счисления в систему с каким-либо другим основанием необходимо:
Непозиционные системы счисления
Непозиционной называется система, в которой число представляется совокупностью узловых и алгебраических чисел. Положение цифры в записи при этом не имеет значения.
Немного истории
Непозиционная система была одной из первых, которую стали использовать люди. Самой древней из них является египетская (2,5-3 тыс. лет до нашей эры). Числа в ней записывались с помощью иероглифов, которые подчинялись «принципу сложения». Аналогичный принцип был у греческой, римской и других систем счисления древности.
Древнеегипетская система
В древнеегипетской системе счисления в качестве цифр использовались единица и десятичные разряды: 10, 100, 1000 и так далее.
Поэтому запись чисел в данной системе была еще более длинной, по сравнению с римской:
Римская система
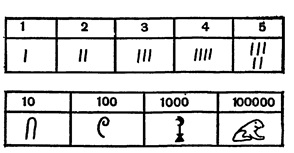
Римские числа знакомы всем еще со школы. Алфавит этой системы счисления состоит из цифр 1, 5 и ряда десятичных разрядов:
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
| I | V | X | L | C | D | M |
Данные основные (узловые) числа используются для записи других чисел путем сложения ли вычитания меньшего числа из большего. При этом числа I, X, C, M не повторяются более трех раз, а V, L, D не могут идти друг за другом вовсе.
Запись больших чисел в такой системе выглядит громоздко:
2589 = 2000 + 500 + 80 + 9 = MM + D + LXXX + IX = MMDLXXXIX
И правильно прочитать его, следует мысленно разбить его на разряды.
Древнегреческая система
В основе данного вида счисления Древней Греции лежал алфавит, схожий с римским:
| 1 | 5 | 10 | 100 | 1000 | 10000 |
| I | Г | Δ | H | X | M |
Затем ему на смену пришел ионийский, который предполагал использование букв греческого алфавита.
Чтобы записать какое-либо число, греки использовали принцип совокупности используемых цифр. Из прочих непозиционных систем греческая является наиболее упрощенной.
Минусы непозиционных систем
Основная сложность работы с данными системами счисления состоит в записи больших чисел. Их написание может быть слишком объемным и сложным для чтения. Если же упрощать запись за счет введения новых цифр, как в греческой системе, требуется создавать большой алфавит, что тоже неудобно.
Непозиционные системы счисления
Здравствуйте, на этой странице рассмотрим одну из важных тем в информатике – а именно непозиционные системы счисления. Здесь вы узнаете, что является непозиционными системами, и познакомитесь с основными определениями, которые относятся к этой теме. Также затронем их отличия от позиционных нумераций и приведем достоинства и недостатки.
Определение непозиционной системы счисления
Непозиционными являются нумерации, где положение цифры в числе (разряд) не влияет на её значение.
Чтобы разобраться конкретно в том, что здесь написано, выберем самое популярное исчисление, которое называется десятичным. Вы все с ним знакомы. Им пользуются люди в большинстве стран мира. Алфавит десятичной нумерации состоит из арабских знаков – чисел от 0 до 9. Данный вид записи является позиционным. Почему, спросите вы? Всё просто. В качестве примера приведем два числа – 1000 и 10. Смотрите на цифру один – в зависимости от того, какое место она занимает в числе, меняется значение, которое она обозначает. В числе 1000 – тысячи, а 10 – десятки.
В непозиционных представлениях все обстоит совсем иначе. Давайте приведем в пример Римскую нотацию. Её вы тоже видели и с ней знакомы. Вспомните – в книгах по истории с помощью неё представляются века и номера монархов. Как пример, Петр I или Иван IV Грозный. Обратите внимание на I и IV, которые в арабском виде запишутся как 1 и 4. Здесь значение единицы не изменяется от того, какое место она занимает. На первом месте она стоит или на втором – неважно.
Историками считается, что исчисления, которые называются непозиционными, ведут свои корни от глубокой древности – это первые формы для счета, которые использовал человек. Поговорим дальше про их виды и разберем недостатки.
Примеры непозиционных систем счисления
Унарная непозиционная
Еще называется непозиционной единичной. Скорее всего, вы уже догадались, почему она так называется. Дело в том, что в этой форме записи используется только один знак. Это представление применяли древнейшие люди. Для записи значений использовались насечки на костях животных или стенах пещеры. Также в обиходе были зарубки на дереве. Используется до сих пор. Вспомните сериалы, где заключенные отсчитывают свои дни в неволе. Также применяется для обучения детей счету – так называемый пальцевый метод.
Унарная сс – отметки на кости
Римская непозиционная
Её мы уже привели выше. Используется до сих пор. В качестве алфавита здесь применяются латинские буквы, такие как V, I, D, M, C, X, L. Всё остальное же получается с помощью различного написания этих символов – здесь используются принципы вычитания и сложения. Так если младший разряд записывается перед старшим, то он вычитается. Если же наоборот, то складывается. Есть у неё и еще одна особенность – нет 0, который является отсутствием числа. Ниже приведена небольшая табличка с расшифровкой римских цифр.
Римское непозиционное счисление появилось в Риме на самом пике процветания империи. Однако и после того как империя распалась этим счислением пользовались еще очень долго. Она использовалась в Европе до 1200х годов, пока великий математик Леонардо Фибоначчи не издал трактат – “Книга Абака”. В нем ученый показывал превосходство позиционных систем над непозиционными.
Египетская непозиционная
Возникла в третьем тысячелетии до нашей эры. Все значения записывались здесь с помощью иероглифов. Каких-то особых правил здесь не существовало – все числовые значения просто складывались. Также не было и правил, которые относятся к записи – последовательность могла быть записана, как слева на право, так и справа налево. Иероглифы могли занимать любой разряд. Ниже приведена табличка со значениями некоторых из них.
Алфавитные системы счисления
Стоит отметить эти формы записи. Здесь все очень просто – каждой букве алфавита сопоставлялась цифра. Стоит отметить, что эти непозиционные системы являются более совершенными, чем все предыдущие, поскольку имелись обозначения десятков и сотен. К недостаткам можно отнести их сложность. Здесь можно выбрать два популярных примера.
Славянская
Использовалась нашими предками во времена древней Руси. Первые записи о ней в летописи временных лет появляются с начала десятого века. Каждой букве глаголицы соответствовало некоторое число. Полностью вышла из использования во времена Российской Империи в восемнадцатом веке, её место заняло десятичное исчисление. Пользуемся мы им, и посей день.
Греческая
Она же называется непозиционной новогреческой или ионийской. Упоминания о ней датируются третьим веком до нашей эры. Здесь счет велся буквами, которые употреблялись в римской письменности. Пришла на смену старогреческому формату. По сути, непозиционное кириллическое представление является её копией.
Достоинства и недостатки. Возможность использования в информатике и других науках.
К достоинствам можно отнести только их простоту. Как мы уже говорили выше, та же унарная непозиционная система применяется для обучения детей. Однако недостатков у них гораздо больше и они очень существенные:
Всё эти недостатки делают их использование в математике и информатике непрактичным.
Заключение
В качестве итогов можно сказать, что после прочтения этого материала вы имеете полное представление о том, что называется непозиционными системами счисления, овладели нужным определением. Знаете виды, которые использовали разные народы в различных частях земного шара. Теперь вы имеете представление о том, как считали люди в Риме, Египте, Греции и древней Руси. Знаете их плюсы и минусы. Понимаете, почему нельзя использовать их в информатике. Как по мне тема достаточно легкая, но очень интересная. При возникновении вопросов задайте их в комментариях к этой записи. Буду рад на них ответить. Также вы можете почитать другие материалы, которые затрагивают информатику на нашем сайте.
Системы счисления. Непозиционные системы счисления.
В непозиционных системах счисления величина, обозначающая цифру, не зависит от положения в числе. К тому же, система может накладывать ограничения на расстановку цифр, например, чтобы цифры располагались по убыванию.
Существуют такие непозиционные системы счисления:
— Единичная система счисления,
— Пятеричная система счисления (Счёт на пятки́),
— Древнеегипетская система счисления,
— Вавилонская система счисления,
— Алфавитные системы счисления,
— Еврейская система счисления,
— Греческая система счисления,
— Римская система счисления,
— Система счисления майя,
Рассмотрим некоторые из, приведенных выше, систем счисления.
Единичная система счисления.
С первых попыток научиться считать у людей возникла необходимость записи чисел. Сначала это было легко — зарубка либо черточка на любой поверхности отвечала за один предмет. Таким образом возникла первая система счисления — единичная.
Число в единичной системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
В более позднее время для упрощения восприятия больших чисел, эти знаки стали группировать по три или по пять. Далее равнообъёмные группы знаков начали заменять новым знаком — так возникли прообразы современных цифр.
У данной системы есть значительные недостатки — чем больше число, тем длиннее строка из палочек. Кроме того, существует большая вероятность в записи числа, пропустив или случайно дописав палочку.
Изначально в счете использовали пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система счисления.
В Древнем Египте использовали свои символы (цифры) для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Вот некоторые из них:
Почему мы ее называем десятичной? Как указано выше — люди начали группировать символы. В Египте — решили группировать по 10, оставив без изменений цифру “1”. Здесь, число 10 называется основанием десятичной системы счисления, а все символы — представление числа 10 в определенной степени.
Числа в древнеегипетской системе счисления записывали, в виде комбинаций таких символов, и все они повторялись не больше 9 раз. Результатом было сумма элементов числа. Этот метод получения значения свойственен каждой непозиционной системе счисления. Для примера посмотрите на запись числа 345:
Вавилонская шестидесятеричная система счисления.
В вавилонской системе счисления использовали только 2 символа: “прямой” клин — для единиц и “лежащий” — для десятков. Для определения значения числа нужно изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. Для примера посмотрим на число 32:
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной системы счисления.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а значения больше 59 — в позиционной с основанием 60. Например, число 92:
Запись числа была не конкретной, так как не было цифры, которая обозначала бы нуль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа они ввели новый символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:
Значит, число 3632 записывают так:
Шестидесятеричная вавилонская система — первая система счисления, которая частично основана на позиционном принципе. Эту систему счисления используют и сейчас, например, для определения времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система счисления.
Римская система счисления немного похожа с египетской. Здесь для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используют заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Способы определения значения числа: