Нелинейная динамика что это

Нелинейная динамика

Нелинейная динамика — междисциплинарная наука, в которой изучаются свойства нелинейных динамических систем. Нелинейная динамика использует для описания систем нелинейные модели, обычно описываемые дифференциальными уравнениями и дискретными отображениями. Нелинейная динамика включает в себя теорию устойчивости, теорию динамического хаоса, эргодическую теорию, теорию интегрируемых систем.

Литература

См. также

Ссылки

Полезное

Смотреть что такое «Нелинейная динамика» в других словарях:

нелинейная динамика — netiesinė dinamika statusas T sritis fizika atitikmenys: angl. non linear dynamics vok. nichtlineare Dynamik, f rus. нелинейная динамика, f pranc. dynamique non linéaire, f … Fizikos terminų žodynas

НЕЛИНЕЙНАЯ ОПТИКА — раздел оптики, охватывающий исследования распространения мощных световых пучков в тв. телах, жидкостях и газах и их вз ствия с в вом. Сильное световое поле изменяет оптич. хар ки среды (показатель преломления, коэфф. поглощения), к рые становятся … Физическая энциклопедия

Динамика — (Dynamics) Содержание Содержание 1. в разных науках В физике В астрономии В науках о Земле В биологии В технике В музыке 2. Динамика в физике 3. Ряды динамики 4. Газовая динамика Динамика – это состояние движения, ход развития, изменение… … Энциклопедия инвестора

Динамика (значения) — Динамика (от греч. δύναμις сила, мощь): Состояние движения, ход развития, изменение какого либо явления под влиянием действующих на него факторов. Системная динамика направление в изучении сложных систем. Содержание 1 В физике … Википедия

Динамика — (от греч. δύναμις сила, мощь): Состояние движения, ход развития, изменение какого либо явления под влиянием действующих на него факторов. Системная динамика направление в изучении сложных систем. Содержание 1 В физике … Википедия

Дробная динамика — Дробная динамика область исследований в физике, механике, математике и экономике, изучающая поведение систем и объектов, для описания которых используются методы интегрирования и дифференцирования дробных порядков, методы дробного… … Википедия

Вольмир — Вольмир, Арнольд Сергеевич Связать? Арнольд Сергеевич Вольмир Место рождени … Википедия

Вольмир, Арнольд Сергеевич — Арнольд Сергеевич Вольмир Место рождения … Википедия

Фурсов Андрей Серафимович — Андрей Серафимович Фурсов Дата рождения: 19 марта 1968(1968 03 19) (43 года) Место рождения: г. Москва Гражданство: РФ … Википедия

Малинецкий, Георгий Геннадиевич — Георгий Геннадиевич Малинецкий Дата рождения: 1956 год(1956) Место рождения: Уфа, БАССР, СССР Страна … Википедия

Источник

Нелинейная динамика и анализ временных рядов – обзор метода Recurrence plots

Всем привет. В этом топике я хотел бы провести обзор относительно нового и довольно мощного метода нелинейной динамики – метода Recurrence plots или рекуррентного анализа в приложении к анализу временных рядов. А, кроме того, поделится кодом короткой программы на языке Matlab, которая реализует все нижеописанное.

Итак, начнем. По долгу службы я занимаюсь нелинейной динамикой, обработкой видео и изображений, я бы даже сказал, довольно узкой частью нелинейной динамики – нелинейными колебаниями роторов. Как известно, вибросигнал представляет собой ничто иное, как временной ряд, где в качестве сигнала выступает значение амплитуды отклонения, ну например, ротора турбины самолета. Как известно, не только колебания ротора можно представить в таком виде. Колебания биржевых котировок, активность Солнца и множество других процессов описываются простым вектором чисел, выстроенным по времени. Скажу даже больше, все эти процессы объединяет один важный фактор – они нелинейны, а некоторые даже хаотичны, что означает на практике невозможность предсказать состояние в системе на сколь угодно большой отрезок времени даже зная точно закон ее движения в виде дифференциальных уравнений. А самое главное, в большинстве случаев мы не можем даже записать эти самые уравнения в каком-либо виде. И тут на помощь приходит эксперимент и нелинейная динамика.

Нелинейная динамика

Снимая показания с датчика (скачивая файл с котировкой валют), мы имеем на выходе одномерный сигнал, как правило, сложной формы. Хорошо еще если сигнал периодический. А если нет? В противном случае мы имеем дело со сложной системой, которая к тому же, может находиться в режиме нелинейных и хаотических колебаний. Под сложной системой в данном случае понимают систему с большим числом степеней свободы. Но мы-то получаем с датчика одномерный сигнал. Как узнать о других степенях свободы этой системы?

Прежде чем мы переедем к главному, стоит упомянуть о еще одном мощном методе анализа нелинейной динамики, который плавно перекочевал в методы анализа временных рядов. Это так называемое восстановление траектории системы по сигналу от всего лишь одной степени свободы. К примеру, вращается по кругу шарик на нити, и если мы смотрим в одной плоскости на это процесс, то сможем снимать сигнал лишь с по одной оси, для нас шарик будет бегать туда-сюда. И вот, выяснилось, что можно полностью восстановить N – мерный сигнал всей системы. Но не в полном объеме, а лишь с сохранением топологических свойств системы (проще говоря ее геометрии). В данном случае, если шарик движется по периодической траектории, то и восстановленная траектория будет периодической. Сам метод основан на простой формуле (в случае двумерной системы):

Y(i) = X(t), Y1(i) = X(t+n), где n – это временная задержка, а Y, Y1 это уже восстановленный сигнал. Доказывается это все в теореме Такенса. В примере пространство двумерно, а в реальности оно может представлять из себя пространство сколь угодно большего числа измерений. Метод оценки размерности пространства не входит в тему данного топика, упомяну лишь о том, что это может быть, к примеру, метод ложных соседей.

Метод Recurrence plots

Итак, мы получили траекторию системы, в которой сохранены топологические свойства реальной физической системы, что очень важно. Теперь мы можем натравить на нее целый арсенал методов распознавания образов для выявления закономерностей. Но все они так или иначе имеют свои недостатки вычислительные или просто сложны в реализации. И вот в 1987 году Экман с коллегами разработали новый метод, суть которого сводиться к следующему. Полученная выше траектория, представляющая собой набор векторов размерности N отображается на двумерную плоскость по формулам:

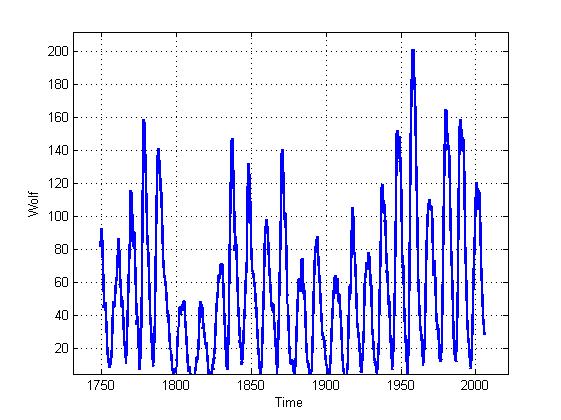
R[i,j,m,e] = O(e[i], — ||S[i] – S[j] ||), где i,j – индексы точки на плоскости, m – размерность пространства вложения, O – функция Хевисайда ||…|| — норма или расстояние (например евклидово). Внешний вид полученной и визуализированной матрицы и даст нам представление о динамике системы, изначально представленной в виде временного ряда. Все вышесказанное проиллюстрируем в виде эксперимента с числами Вольфа, которые описывают активность Солнца (вместо этого ряда легко можно взять котировки валют).

Результаты

Это собственно сам сигнал:

Это восстановленная траектория в двумерном пространстве (мы берем двумерное пространство для простоты, хотя на самом оно содержит большее число измерений, но как показывает практика этого вполне достаточно для качественной оценки)

Это так называемая матрица расстояний (по смыслу всего лишь расстояния от i-ой точки доя j-ой). Часто эти диаграммы имеют замысловатый рисунок, что может быть использовано (и используется) в дизайне.

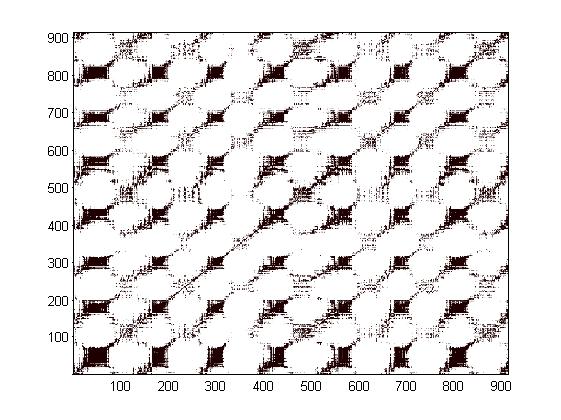
Ну вот собственно и сама рекуррентная диаграмма. Для описания всех методов анализа такой диаграммы не хватит и 400 страниц. Помимо качественного анализа, данный метод допускает и количественные показатели, что может с успехом использоваться в случае использования нейронных сетей. Ну а самое важное, это то, что уже бросив беглый взгляд на эту диаграмму, мы можем сказать о ней многое. Во-первых наличие полос, которые перпендикулярны главной диагонали говорит о наличии хаотического или стохастического процессов в системе (что бы сказать точно необходимы дополнительные исследования). Наличие неравномерно заполненных черными точками зон говорит о нестационарных процессах и позволяет точно определить границы этих процессов во времени.

Код в Matlab

PS. Это всего лишь элементарный пример, который, естественно, не охватывает всю мощь этого метода. В простейшем случае для автоматизации процесса вы можете использовать алгоритмы поиска фигур на плоскости. Такие системы могут быть актуальны в системах мониторинга турбин самолета, а так же системах мониторинга различных финансовых процессов. Я не затронул самую интересную часть данной тематики — вычисление количественных показателей этих диаграмм, что постараюсь компенсировать в ближайших топиках.

Источник

Нелинейная динамика что это

Первоначально понимание сложных систем (например таких, как биологические) было связано с представлением о том, что их невозможно описать при помощи математических моделей. Более того, долгое время жизнь рассматривалась как антипод неорганической природы. Сегодня, однако, происходит все более активное проникновение физических методов и подходов в биологию. Оказывается также, что основные формы кооперативного поведения, свойственные живым организмам, имеют свои аналоги среди неорганических систем. Любой живой организм представляет собой иерархию достаточно автономных подсистем, в которой исходящие от верхнего уровня сигналы управления не имеют характера жестких команд, подчиняющих себе активность всех индивидуальных элементов более низких уровней. Вместо этого от высших уровней иерархии поступают сигналы, которые предопределяют переходы подсистем от одного режима функционирования к другому.

Самоорганизация

Первоначально понимание сложных систем (например таких, как биологические) было связано с представлением о том, что их невозможно описать при помощи математических моделей. Более того, долгое время жизнь рассматривалась как антипод неорганической природы. Сегодня, однако, происходит все более активное проникновение физических методов и подходов в биологию. Оказывается также, что основные формы кооперативного поведения, свойственные живым организмам, имеют свои аналоги среди неорганических систем. Любой живой организм представляет собой иерархию достаточно автономных подсистем, в которой исходящие от верхнего уровня сигналы управления не имеют характера жестких команд, подчиняющих себе активность всех индивидуальных элементов более низких уровней. Вместо этого от высших уровней иерархии поступают сигналы, которые предопределяют переходы подсистем от одного режима функционирования к другому. Иерархическое устройство сложных живых систем, представляющих собой ансамбль связанных подсистем более простого строения, позволяет избежать неустойчивостей и нежелательной динамики, которые неизбежно возникают в сложных системах с жестким централизованным управлением.

Наиболее очевидная особенность биологических систем заключается в том, что они способны к самоорганизации, то есть спонтанному образованию и развитию сложных упорядоченных структур. Это не противоречит законам термодинамики, поскольку все живые биологические системы не являются замкнутыми и обмениваются энергией с окружающей средой. Энтропия, служащая мерой беспорядка, может уменьшаться в открытых системах с течением времени. Необходимая предпосылка эффектов самоорганизации заключается, кроме того, в наличии потока энергии, поступающего в систему от внешнего источника и диссипируемого ею. Именно благодаря этому потоку система становится активной, то есть приобретает способность к автономному образованию структур. Очевидно, что эффекты самоорганизации не могут быть исключительным свойством биологических объектов и должны наблюдаться в той или иной форме также в системах неорганического происхождения.

Большой интерес представляют распределенные среды, которые построены из дискретных элементов, локально взаимодействующих друг с другом и, таким образом, представляющих приближение естественных пространственно протяженных систем. Хотя разнообразие таких сред чрезвычайно велико, число математических моделей, используюемых для описания процессов образования и развития структур в таких системах, не столь значительно. По-видимому, даже когда отдельные элементы системы (например, живые клетки) обладают сложной внутренней структурой, вся их сложность не проявляется во взаимодействиях между ними, и с точки зрения макросистемы они функционируют как достаточно простые объекты с малым числом эффективных степеней свободы. В противном случае никаких упорядоченных структур в системе обычно не возникает.

Задача нелинейной динамики и синергетики состоит в нахождении и подробном исследовании тех базовых математических моделей, которые исходят из наиболее типичных предположений о свойствах отдельных элементов, составляющих систему, и законах взаимодействия между ними. Поскольку главным отличительным свойством изучаемых сред являются протекающие в них процессы самоорганизации, синергетику можно также рассматривать как общую теорию самоорганизации в средах различной природы. Термин «синергетика» (от греч. synergeia — совместное действие, сотрудничество) был предложен в начале 70-х годов немецким физиком Г. Хакеном.

Динамический хаос

Где лежит граница между регулярной, но сложно организованной структурой (то есть порядком) и беспорядком? Часто под беспорядком подразумевается проявление системой качественно нового режима — хаоса. Критерием появления такого режима может служить устойчивость возникающих в системе образований по отношению к малым возмущениям. Если такая устойчивость отсутствует, детерминированное описание теряет смысл, и необходимо использовать статистические методы.

Однако, как показали многочисленные исследования, статистические законы, а вместе с ними и статистическое описание относятся не только к очень сложным системам с большим числом степеней свободы. Дело здесь не в сложности исследуемой системы и не во внешних шумах, а в появлении при некоторых значениях параметров экспоненциальной неустойчивости движения.

Впервые эта концепция получила строгое обоснование на простейшей модели статистической механики — бильярде (рис. 1). Хорошо известно, что к системам, отвечающим бильярдам, сводится ряд задач статистической физики. По существу, математический плоский бильярд представляет собой обычный бильярд, только с произвольной конфигурацией стола и без луз. Оказывается, что в зависимости от формы границы даже чисто детерминированная система из двух шаров (!) может обладать свойством хаотичности

Какие же законы управляют хаосом? Возможно ли создать математический аппарат, позволяющий непротиворечиво описывать хаотическую динамику и предсказывать появление хаоса в тех или иных системах? Наконец, можно ли найти методы предсказания поведения хаотических систем? Ответами на эти и ряд других вопросов занимается так называемая теория динамического (или детерминированного) хаоса, являющаяся одним из разделов нелинейной динамики. К настоящему времени разработаны методы классификации различных типов хаоса, найдены закономерности его развития, созданы техники, позволяющие отличить (например, в эксперименте) хаос от белого шума, и т. п. Более того, было обнаружено и строго обосновано, что сложное пространственно-временное поведение распределенных сред с громадным числом степеней свободы может быть адекватно описано нелинейными системами небольшой размерности.

Как известно, математическим образом установившихся периодических колебаний является предельный цикл. Простым примером здесь может служить обычный часовой маятник.

Циклы могут быть устойчивыми и неустойчивыми. Устойчивые циклы являются примерами аттракторов, поскольку они «притягивают» все близкие траектории. Физически это означает, что при отклонении от таких колебаний система спустя некоторое время вновь возвращается к ним. Колебания маятника — устойчивый цикл.

Если же система проявляет хаотические свойства, это соответствует наличию в ее фазовом пространстве более сложного, чем цикл, образования: странного (иногда говорят: хаотического) аттрактора. Странный аттрактор — это множество очень сложной геометрии, к которому притягиваются проходящие вблизи от него траектории. Данное понятие впервые было введено в известной работе Д. Рюэля и Ф. Такенса «О природе турбулентности» в 1971 году.

Исследования нелинейных динамических процессов в математике и физике показали, что хаотическое поведение в системах с небольшим числом степеней свободы весьма типично. Таким образом, проблема предсказуемости стала общей для многих направлений современной науки. В связи с этим в последнее время стало интенсивно развиваться новое направление в нелинейной динамике и синергетике, посвященное проблемам предсказуемости поведения хаотических систем, управления их динамикой и возможности подавления хаоса. На этом пути удается найти подходы к таким приложениям, как обработка информации, скрытая связь (то есть пересылка зашифрованных сообщений), стабилизация неупорядоченных сокращений сердечной мышцы и дефибрилляция, прогноз динамики финансовых рынков и др.

Стабилизация хаотических колебаний и обработка информации

Хаотические динамические системы имеют замечательное свойство: они весьма податливы и чрезвычайно чувствительны к внешним воздействиям. Более того, динамикой хаотических систем можно управлять, то есть посредством слабых воздействий переводить такие системы из режима хаотических колебаний на требуемый динамический режим (тем самым, стабилизируя их поведение). Существует два основных способа стабилизации: без обратной связи и с обратной связью. Первый способ называется подавлением хаоса, второй — контролированием хаоса (controlling chaos).

Методы хаотической динамики дают возможность при относительно малых энергетических затратах создать устройства принципиально нового типа, способные запоминать, шифровать и обрабатывать заданную информацию. Один из подходов к этому основан на том, что хаотические аттракторы содержат, как правило, бесконечное множество неустойчивых циклов. Для ряда систем разработаны методы, позволяющие либо стабилизировать эти циклы, либо создавать новые. Это является ключом к решению проблемы обработки информации и организации динамической памяти на основе использования систем с подавленным хаосом.

Рассмотрим динамическую систему с хаотическим аттрактором. В такой системе предельные циклы будут неустойчивыми. Каждому элементу алфавита поставим в соответствие один из циклов. В типичном хаотическом аттракторе имеется неограниченное число неустойчивых циклов. Значит, в принципе (без учета шума) таким способом может быть закодировано неограниченное число слов, причем записанная информация будет скрыта, ибо неустойчивые циклы практически ненаблюдаемы. Однако систему можно возмутить так, что нужный нам цикл станет устойчивым. Это позволяет извлечь закодированную информацию.

Опишем одну из реализаций этой идеи. Возьмем какую-либо динамическую систему с хаотическим аттрактором. Поставим в соответствие каждому стабилизированному (с помощью некоторого возмущения) циклу определенный символ алфавита. Вместо символа мы передаем на приемник стабилизирующее возмущение. Приняв возмущение, приемник применяет его к «зашитой» в нем той же самой динамической системе, и «смотрит», какой цикл при этом возник. А возникнет, разумеется, тот самый цикл, который обозначен переданным символом.

Но какая разница — передать сам символ или возмущение, стабилизирующее соответствующий ему цикл? Во-первых, для многих хаотических систем можно разработать эффективный сценарий поиска возмущений, приводящих к стабилизации цикла, проходящего через заданные точки. Эти точки можно выбрать случайным образом — тогда и стабилизирующее возмущение будет выглядеть как случайная последовательность параметров. Во-вторых, в ряде систем одному и тому же циклу (то есть символу) соответствует не одно, а целая область стабилизирующих возмущений. При каждой передаче этого символа можно выбирать параметры из этой области тоже случайным образом! Поэтому в передаваемой последовательности не будет повторений, связанных с кодированием идентичных символов алфавита, и отличить этот сигнал от шума будет невозможно; к тому же «противнику» для расшифровки необходимо знать конкретный вид динамической системы, который в данном случае является ключом.

Предлагаемый метод был реализован на компьютере на основе квадратичной дискретной динамической системы, действие которой состоит в итеративном применении отображения

(параметр a принадлежит интервалу (0,4]). Он позволил создать экспериментальную систему шифрования символов, вводимых с клавиатуры персонального компьютера. Кратко опишем эту систему.

При использовании компьютера типа IBM PC с операционной системой MS-DOS каждый символ, вводимый с клавиатуры, кодируется целым числом (ASCII-кодом), принадлежащим отрезку [0,255]. Каждому символу можно поставить в соответствие последовательность из трех целых чисел — десятичных цифр ASCII-кода n1, n2, n3. Например, символу A с ASCII-кодом 65 отвечает тройка чисел n1 = 0, n2 = 6, n3 = 5. Каждому из этих трех чисел ставится в соответствие последовательность параметров, стабилизирующая цикл периода ni + 2. Полученная в результате такого кодирования последовательность транслируется на приемник, в котором находится дешифратор. На дешифраторе последовательность параметров преобразуется в последовательность целых чисел, соответствующих периодам циклов. Из каждого полученного целого числа необходимо вычесть 2. Теперь, сгруппировав эти числа по три, легко получить ASCII-код символа и, таким образом, сам символ.

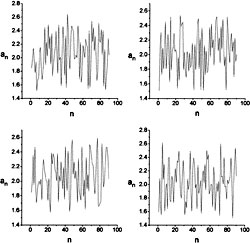
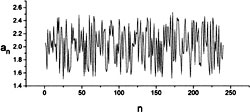
Результаты работы кодирующей программы представлены на рис. 2. и 3. На рис. 2 изображены четыре различных варианта кодирующих последовательностей параметров для слова CHAOS. На рис. 3 графически представлена последовательность параметров, кодирующая строку из десяти одинаковых символов «c».

Временные ряды

Наиболее интригующим и заманчивым приложением теории нелинейных систем с хаотическим поведением является прогнозирование динамики порождаемых ими временных рядов. Как известно, большинство систем (природных, таких, например, как атмосфера, или искусственных, таких, например, как биржа), в силу их сложности, не могут быть смоделированы с достаточной точностью. Однако их можно описать на основе наблюдения за ними. Наблюдаемая (сигнал, реализация) — это функция от времени, по которой судят о процессе в исследуемой системе. Иными словами, наблюдаемая — это временной ряд. Например, для атмосферы в качестве наблюдаемой может выступать изменение температуры, для биржи — ежедневный курс ценных бумаг и т. п. Если такую наблюдаемую определенным образом обработать, при некоторых условиях возможно с большой точностью произвести оценку будущего значения временного ряда, зная только (!) предыдущие значения. Наблюдаемой может быть курс доллара, сейсмозапись или динамика солнечной активности. При этом оказывается, что методы теории вероятностей зачастую работают хуже, чем методы теории динамических систем.

При каких условиях возможен такой прогноз? В рамках современной теории размерности и теории динамических систем можно, в принципе, отличить шум (случайный процесс) от детерминированного поведения. Опираясь на некоторые дополнительные определения, для наблюдаемой можно определить так называемую размерность (емкость). Если окажется, что емкость — величина конечная, то (при выполнении еще ряда условий) наблюдаемая описывается конечномерной системой обыкновенных дифференциальных уравнений. Если далее удается (хотя бы частично) восстановить явный вид этих уравнений, то прогнозирование становится возможным. Таким образом, по единственной наблюдаемой, в принципе, возможно восстановить многие свойства поведения динамической системы и получить представление о ее аттракторе.

Динамическое моделирование финансовых временных рядов

В последнее время все большее внимание уделяется исследованию и прогнозированию финансовых временных рядов с использованием теории динамических систем. Это достаточно новая область, которая представляет собой популярный и активно развивающийся раздел математических методов экономики.

Финансовый временной ряд — это последовательность, описывающая поведение определенного рыночного процесса, например, курс ценных бумаг или соотношение валют. В ряде работ был проведен анализ некоторых финансовых рядов и показано, что многие из них имеют конечную емкость. Таким образом, эти ряды могут быть описаны обыкновенным дифференциальным уравнением конечного порядка. Для прогнозирования динамики временного ряда нужно восстановить «правую часть» этого уравнения. В некоторых работах проводились оценки длины временного ряда, необходимой для такого восстановления. Оценки показывают, что в большинстве случаев имеющихся данных недостаточно.

Для решения этой проблемы можно предложить несколько подходов. Остановимся на одном из них, который использует модели формирования цен финансовых активов, созданные в теории финансов. Это в ряде случаев может дать вид искомых уравнений. После этого остается определить значения нескольких параметров, которые ищутся из условия оптимального приближения решения уравнения к имеющимся данным. Такая методика иногда позволяет сократить объем необходимых для прогнозирования данных на порядки.

Восстановленные дифференциальные уравнения определяются на основе следующих допущений.

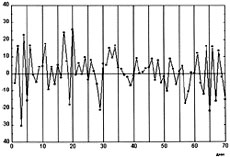
Инвесторы имеют разный горизонт инвестирования. Иными словами, некоторые инвесторы (спекулянты) оценивают активы с точки зрения их краткосрочной (несколько дней) доходности; другие (стратегические инвесторы) ориентированы на получение дохода в долгосрочной перспективе (несколько лет). Между этими крайними случаями также существует непрерывный спектр инвесторов. Кроме того, необходимо сделать еще несколько (вполне реалистических) допущений о конкретном виде ряда зависимостей: как инвесторы определяют доходность своих активов, как меняются со временем финансовые возможности инвесторов и т. д. В совокупности, все эти допущения позволяют довести моделирование до замкнутого дифференциального уравнения и неплохо прогнозировать некоторые временные ряды. В качестве примера рассмотрим курс акций компании IBM. На рис. 4 показана разность между значениями этого ряда и рассчитанными из построенной модели величинами. Прогнозируемое значение ряда отличается от реального не более чем на 35 процентов. Следует учесть, что, во-первых, выбранный временной ряд является очень коротким, то есть фактически имеются сильно ограниченные сведения о его динамике; во-вторых, влияние начальных условий весьма велико; в-третьих, на торги могут влиять какие-то внешние условия, не включенные в модель.

Рис. 4.

Таким образом, при выполнении определенных предпосылок можно предложить достаточно эффективный механизм описания коротких финансовых временных рядов. Существуют и другие подходы к моделированию и прогнозированию таких рядов, использующие более тонкие методы теории динамических систем, но объем статьи не позволяет их здесь рассмотреть.

Подавление хаоса и сердечная аритмия

Знание закономерностей самоорганизации дает возможность управлять динамикой реальных биосистем. Недавно открыты принципиально новые методы стабилизации работы сердца при появлении аритмий, а также смертельно опасных фибрилляций.

Сердечная мышца (как и любая другая мышечная ткань) относится к так называемым возбудимым системам. При подаче импульса в такую систему от места его приложения начинает распространяться возмущение — волна возбуждения: поступивший импульс передается от элемента к элементу. Обычно после возбуждения каждый элемент не способен сразу же возбудиться вновь. Как правило, существует определенное «время релаксации», называемое периодом рефрактерности, во время которого элемент как бы восстанавливается. Это приводит, с одной стороны, к упорядоченному пространственному распространению волны возбуждения, а с другой стороны, при частой подаче импульсов (или при большом периоде рефрактерности) часть из них окажется блокированной.

При описании ряда возбудимых сред часто прибегают к аппроксимации исходной системы совокупностью отдельных возбудимых элементов, локально взаимодействующих друг с другом. Каждый такой элемент способен находиться в одном из трех состояний — покоя, возбуждения и рефрактерности. Из состояния покоя элемент может перейти в возбужденное состояние, в котором будет находиться определенное время. Затем он переходит в состояние рефрактерности и только потом вновь в состояние покоя. Таким образом, переход в возбужденное состояние оказывается возможным лишь из состояния покоя. Хотя такая модель является определенным приближением, она очень хорошо воспроизводит основные явления в возбудимых средах, в том числе и тканях сердца.

Предположим, что имеется однородная возбудимая среда, в которой все элементы обладают идентичными свойствами. Тогда частота возбуждения всех таких элементов будет одинаковой. Если некоторую область такой среды начать периодически возмущать, то в этой области возникнет источник концентрически расходящихся волн возбуждения. Такой источник называют ведущим центром, или пейсмекером (рис. 5). Если в возбудимой среде есть два или несколько пейсмекеров, то пейсмекер меньшей частоты генерации с течением времени подавляется пейсмекером большей частоты. Иными словами, имеет место конкуренция между пейсмекерами. В идеальном случае через определенное время во всей среде останется только один пейсмекер. Кроме пейсмекеров, в возбудимых средах возможно появление иных источников возбуждения — спиральных волн, которые представляют собой «вращающиеся» спирали (рис. 6). Все спиральные волны имеют одинаковую частоту. Поэтому они всегда сосуществуют между собой, но гасят ведущий центр, являющийся более медленным автоволновым источником. Кроме того, спиральные волны представляют собой главный тип элементарных самоподдерживающихся структур в однородных возбудимых средах. Подобно вихрям в сверхпроводнике или сверхтекучем гелии, они чрезвычайно устойчивы. Появление нескольких источников возбуждения в сердечной мышце в настоящее время связывается с опасными нарушениями нормальной работы сердца — аритмией. При большом числе аномальных источников наступает фибрилляция.

Допустим, что в некоторой среде имеются только основной и дополнительные ведущие центры. Даже такая простая ситуация в зависимости от частоты поступления импульсов и времени рефрактерности может привести к очень сложному поведению среды. В частности, может возникать хаотическая динамика.

Причиной некоторых нарушений нормальной работы сердца может служить взаимодействие и конкуренция между нормальным («естественным») ведущим центром и аномальным (то есть дополнительным) центром, который по тем или иным причинам может возникать в сердечной ткани. Нормальный ведущий центр называется синусным центром (узлом), а аномальный — смещенным. Нормальный центр находится в правом предсердии, а смещенный — в желудочке. Эти два центра участвуют в работе сердца, и их взаимодействие приводит к нарушению ритмичных сокращений.

Как показывают исследования, такого рода аритмии могут быть эффективно описаны относительно несложными динамическими системами. Методы управления такими системами, о которых речь шла выше, позволяют ожидать, что вполне возможно практически воплотить идею вывода сердечной мышцы с данной патологией на требуемый режим. По-видимому, необходимо лишь подобрать внешние возмущения небольшой амплитуды и соответствующей частоты.

Много более опасное нарушение сердечного ритма — фибрилляции — обусловлено появлением, вследствие различных причин, множества небольших волн в сердечной ткани. Например, могут возникать спиральные волны, вращающиеся в противоположных направлениях.

Современные методы выведения сердца из состояния фибрилляции являются очень жесткими (подача короткого электрического импульса громадного напряжения и большого тока). Развитие нелинейной динамики и синергетики позволило понять, что такое силовое воздействие вовсе не обязательно. Часто вполне достаточно слабых электрических воздействий непосредственно на сердечную мышцу. Именно, если в среде имеются спиральные волны с противоположными направлениями вращения, то, подбирая фазу и частоту внешнего воздействия, можно добиться движения центров двух волн навстречу друг другу и их аннигиляции. Недавно эта задача была математически исследована достаточно полно. Теперь слово за тщательными экспериментальными исследованиями.

Литература
[1] Лоскутов А. Ю., Михайлов А. С. Введение в синергетику. — М.: «Наука», 1990.

[2] Jackson E. A. Perspectives of Nonlinear Dynamics. Vol. I, II. — Cambridge Univ. Press, Cambridge, 1989, 1990.

[3] Manneville P. Dissipative Structures and Weak Turbulence. — Academic Press, London, 1990.

[4] Шустер Г. Детерминированный хаос. Введение. — М.: «Мир», 1988.

[5] Берже П., Помо И., Видаль К. Порядок в хаосе. — М.: «Мир», 1991.

[6] Ахромеева Т. С., Курдюмов С. П., Малинецкий Г. Г., Самарский А. А.. Нестационарные структуры и диффузионный хаос. — М.: «Наука», 1992.

[7] Loskutov A. Chaotic dynamics of chemical systems. — In: Mathematical Methods in Contemporary Chemistry. Ed. S. I. Kuchanov. — Gordon and Breach, USA, 1995, p. 181-265.

[8] Mikhailov A. S., Loskutov A. Yu. Chaos and Noise. — Springer, Berlin, 1996.

[9] Гласс Л., МэкиМ. От часов к хаосу. Ритмы жизни. — М.: «Мир», 1991.

[10] Журнал «Физическая мысль России». 1997, т. 2/3, стр. 1-112.

Автор: АЛЕКСАНДР ЛОСКУТОВ биография и другие статьи автора
Рубрика: «ТЕМА НОМЕРА» еще статьи из рубрики

Источник