О чем говорит теорема бабине
Принцип Бабине
Вы будете перенаправлены на Автор24
Принцип или теорема Бабине является следствием гипотезы Френеля. Он связывает дифракционные поля для некоторого экрана с полями для дополнительного экрана.
Описанные выше экраны называют дополнительными если:
Например, подобными экранами могут быть два непрозрачных экрана, имеющие отверстия. Отверстия одного экрана не совпадают с отверстиями другого. Или говорят, что отверстия одного экрана совпадают с непрозрачными частями другого экрана. Так, дополнительным экраном называют экран, который получают заменой отверстий на экран, а экрана на отверстия.
Сложим выражения (4), учитывая (3), имеем:
Применение принципа Бабине к случаю дифракции Фраунгофера
Допустим, что мы наблюдаем фраунгоферовскую дифракционную картину в фокальной плоскости линзы. Если на пути параллельных лучей нет препятствия, то световое поле в данной плоскости везде равно нулю за исключением фокуса линзы. Так, в соответствии с формулой (6) в любой точке фокальной плоскости за исключением фокуса мы имеем:
Готовые работы на аналогичную тему
Для наблюдения доступна интенсивность поля света, а не его фаза, получаем, что фраунгоферовы дифракционные картины от дополнительных экранов, которые получаются в фокальной плоскости линзы, везде одинаковы, исключение составляет фокус.
Принцип Бабине выполняется не точно, в некотором приближении, но нарушение считают существенным только около границ диафрагм.
Задание: Покажите, что количество энергии рассеяния равно энергии, которая поглощается черным экраном, если на него падает плоская волна света. В результате дифракции за экраном вместе с неотклонённой волной возникает рассеянный свет. Считайте, что размеры экрана велики в сравнении с длиной волны.
Решение:
В соответствии с законами геометрической оптики при освещении черного экрана светом за ним должна образоваться область геометрической тени, площадь этой тени должна быть равна площади экрана в направлении перпендикулярном к направлению падения света. Однако существование явления дифракции ведет к частичному отклонению света от первоначального направления распространения. Так, на большом расстоянии, позади экрана тень отсутствует. Вместе со светом, который распространялся в начальном направлении, присутствует некоторое количество света под малыми углами к первоначальному направлению (рассеянного света).
Проведем замену исходного экрана дополнительным, то есть отверстием той же величины и формы. В результате такой замены по теореме Бабине интенсивность поля света в бесконечности не изменится во всех направлениях, исключение составит направление первичной волны. Однако следует заметить, что на любое жестко фиксированное направление за отверстием приходит нулевая интенсивность света, так отверстие рассеивает весь свет, который на него падает. С другой стороны, экран по условию поглощает полностью весь падающий на него свет, так как является черным. Получаем, что полное количество рассеянного света на черном теле равно количеству света, которое падает на его поверхность и поглощенного им. Следовательно, мы получили, что требовалось показать.
Решение:
Если источником плоской волны является лазер, размеры пучка излучения много меньше ширины щели, то без препятствий на экране будем иметь яркое световое пятно. В остальной области экрана поле световой волны монжо принять равным нулю. Для этой области (без пятна), можно записать:
Соответственно для интенсивностей:
В области основного пятна имеем:
\[I_
Получаем, что для щели и проволоки, обладающих одинаковыми размерами, распределение интенсивностей на экране одинаково везде, кроме места, где попадает исходный пучок лазера, если препятствия нет. Если толщина проволоки равна размеру первого максимума дифракции для щели (помним, что их размеры одинаковы), то для обоих объектов исследования совпадают координаты всех минимумов и максимумов картины дифракции.
При дифракции на проволоке помимо минимумов, которые соответствуют минимумам дифракции на щели, можно увидеть еще два резких минимума в области уменьшения интенсивности лазерного пучка. Это объяснимо при использовании принципа Бабине. Так, в области пучка лазера выполняется соотношение:
Данная точка ($
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 18 03 2021
Принцип Бабине
Принцип (теорема) Бабине
Принцип (теорема) Бабине о свойствах дополнительных экранов является следствием гипотезы Френеля.
Выше названные экраны называют дополнительными, если выполняется условие:
Примером дополнительных экранов могут служить два экрана, имеющих отверстия, если отверстия на одном экране совпадают с непрозрачными участками второго экрана.
При суммировании выражений (3) и (4) получаем:
Выражение (6) принцип Бабине в скалярном виде.
Рассмотри дифракцию Фраунгофера. Пусть на пути распространения параллельных лучей отсутствуют любые препятствия, тогда световое поле в фокальной плоскости линзы будет равно нулю всюду, за исключением фокуса. В таком случае по теореме Бабине (6) мы получим в каждой точке рассматриваемой плоскости (не в фокусе линзы) равенство:
Равенство (8) означает, что картины дифракции при рассматриваемом явлении в фокальной плоскости линзы всюду одинаковые, исключением является фокус.
Теорема Бабине не является строгим утверждением, но ее нарушения являются существенными только у границ, рядом с которыми происходит дифракция. Представленная формулировка теоремы не всегда является удовлетворительной, так как она относится к скалярным полям и основана на приближении Кирхгофа.
Примеры задач с решением
Решение. Следуя условиям задачи и согласно принципу Бабине можно записать следующие соотношения между полями, приведенными в условиях:
Данные соотношения являются векторным аналогом скалярного принципа Бабине. Для плоской волны, которая падает на дифракционный экран, получаем, что в направлениях, которые не совпадают с направлениями падения волны, интенсивности поля дифракции для экрана и его дополнений одинаковы. При этом сами поля связывают соотношения:
Задание. Приведите пример, в котором следует использовать строгую векторную формулировку принципа Бабине.
Принцип Бабине не по зубам? Тебе ответит эксперт через 10 минут!
О чем говорит теорема бабине
Прежде чем переходить к рассмотрению отдельных примеров дифракции, установим одно полезное соотношение, так называемый принцип Бабине. Принцип Бабинё связывает дифракционные поля для некоторого экрана с полями для дополнительного экрана.
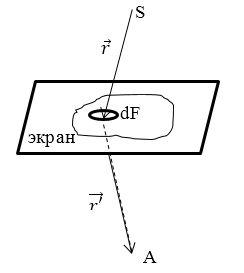
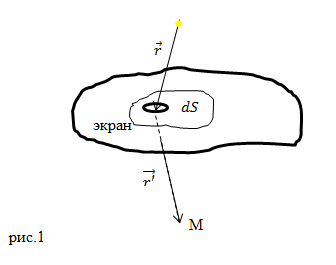
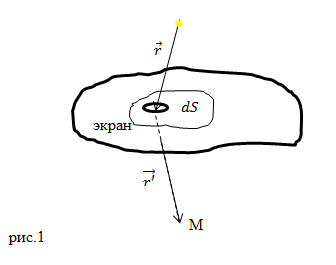
Фиг. 9.7. Дифракционный экран 
и дополнительный к нему экран 
Рассмотрим сначала этот принцип, ограничиваясь скалярным приближением Кирхгофа. Дифракционный экран предполагается расположенным на некоторой поверхности S, разделяющей пространство на области I и II так же, как и в § 5. Пусть экран занимает всю поверхность S, за исключением некоторых отверстий. Дополнительным экраном называется экран, получающийся из первоначального заменой отверстий на экран, а экрана на отверстия. Обозначим поверхность исходного экрана через 
а дополнительного — через 
тогда 
как схематически показано на фиг. 9.7.
Если внутри S (в области I) имеются источники поля 
то в отсутствие каких-либо экранов это поле в области II дается интегралом Кирхгофа (9.65), где интегрирование производится по всей поверхности S. Если же на поверхности S расположен экран 
то поле 
в области II в приближении Кирхгофа дается интегралом (9.65), в подынтегральном выражении которого стоит
то же поле 
но интеграл берется только по 
(по отверстиям). Аналогично для дополнительного экрана поле 
в том же приближении дается интегралом по 
Отсюда очевидно следующее соотношение между дифрагированными полями 
Это и есть принцип Бабине, как его обычно формулируют в оптике. Если, например, 
представляет собой падающую плоскую волну, то, согласно принципу Бабине, дифракционная картина в направлениях, отличных от направления прямого падения, одинакова для взаимно дополнительных экранов.
Полученная формулировка принципа Бабине неудовлетворительна в двух отношениях: во-первых, она относится к скалярным полям и, во-вторых, основана на приближении Кирхгофа. Второй недостаток можно устранить, если мы обобщим определение дополнительности и при замене экрана на дополнительный экран введем и дополнительные граничные условия (т. е. условия Дирихле заменим на условия Неймана, и наоборот) для скалярных полей. Однако, поскольку нас в основном интересуют электромагнитные поля, мы не будем больше останавливаться на скалярной задаче.
Строгую формулировку принципа Бабине для электромагнитных волн можно получить для случая тонкого плоского идеально проводящего экрана и дополнительного к нему экрана. Пусть поля 
падают на экран с металлической поверхностью 
(см. фиг. 9.7), расположенный в свободном пространстве. Вследствие наличия экрана образуются проходящие и отраженные волны, как показано на фиг. 9.4. В дальнейшем в тех случаях, когда нам не потребуется более детального разделения, мы будем объединять проходящие и отраженные волны под общим названием рассеянных волн 
. В случае идеально проводящего экрана поверхностный ток К, индуцируемый падающей волной, должен быть таким, чтобы во всех точках поверхности экрана 
выполнялось равенство 
Для тонкой плоской поверхности из симметрии задачи следует, что тангенциальные составляющие рассеянных магнитных полей на поверхности должны быть равны и противоположно направлены. Согласно (5.90), имеем
где нормаль 
направлена в сторону области 
. С помощью тех же рассуждений, что и при выводе (9.80) из (9.79), можно показать,
что для любой точки 
в области II и ее зеркального изображения 
в области 
рассеянные поля удовлетворяют следующим условиям симметрии:
Заметим, что эти соотношения отличаются от (9.80) заменой знаков 
на обратные. Как показано в книге Смайта [100], поля (9.80) соответствуют двойному токовому слою, тогда как поля (9.85) обладают симметрией, характерной для простого плоского токового слоя, излучающего в обоих направлениях.
Мы можем написать выражение для рассеянного магнитного поля в виде интеграла по поверхностным токам К. Поскольку В есть ротор векторного потенциала, то
где G — функция Грина (9.66), а интегрирование производится по металлической поверхности экрана 
Подставляя К из (9.84), мы можем записать магнитное поле в области II в виде
Этот результат аналогичен (9.82) с той разницей, что
1) поля Е и В поменялись местами;
2) здесь интегрирование производится только по поверхности экрана, тогда как в (9.82) — только по площади отверстий;
3) в выражение (9.82) входит полное электрическое поле, тогда как в (9.87) входит только рассеянное поле.
Сопоставление (9.87) с (9.82) позволяет сформулировать принцип Бабине. Запишем соотношение (9.82) для экрана, дополнительного к рассматриваемому экрану с металлической поверхностью
Здесь интеграл берется только по поверхности 
поскольку она соответствует отверстиям в дополнительном экране. В области II поле Е представляется суммой
где 
падающее электрическое поле в дополнительной дифракционной задаче, 
соответствующее проходящее, или дифрагированное, поле. Очевидно, выражения (9.87) и (9.88) переходят одно в другое при замене
Легко показать, что справедливо также соотношение
Отличие в знаках объясняется тем, что в обоих случаях поля должны представлять собой уходящие волны. Поскольку мы могли принять в качестве исходного дополнительный экран, то соотношения (9.90) и (9.91) должны быть справедливы и при замене штрихованных величин на нештрихованные и наоборот. Сравнение получающейся системы равенств с первоначальной показывает, что падающие поля в исходной и дополнительной дифракционных задачах должны быть связаны соотношениями
Дополнительная задача соответствует не только дополнительному экрану, но также и дополнительным падающим полям, в которых Е и В меняются местами.
Таким образом, принцип Бабине формулируется следующим образом: пусть дифракционная система состоит из источников, создающих поля 
падающие на тонкий плоский идеально проводящий экран с отверстиями. Дополнительная к ней дифракционная система состоит из источников, дающих поля 
падающие на дополнительный экран. Если проходящие (дифрагированные) поля за экраном (со стороны, противоположной источникам) равны Е, В для основной системы и 
для дополнительной, то имеют место следующие соотношения:
Эти соотношения являются векторным аналогом скалярного принципа Бабине (9.83). Для плоской волны, падающей на дифракционный экран, из принципа Бабине следует, что в направлениях, отличных от направления падения, интенсивности дифракционного поля для экрана и его дополнения одинаковы, а сами поля связаны соотношениями
Поляризация падающей волны для дополнительного экрана должна быть, конечно, изменена согласно (9.92).
Строгая векторная формулировка принципа Бабине очень полезна для микроволновых задач. Рассмотрим, например, узкую щель, прорезанную в бесконечной плоской проводящей пластине, на которую падает волна с магнитным полем, направленным вдоль щели, и с электрическим полем, перпендикулярным щели, как показано на фиг. 9.8.
Фиг. 9.8. Эквивалентные излучающие системы в соответствии с принципом Бабине.
Диаграмма излучения этой щели будет такая же, как и для тонкой линейной антенны, электрическое поле в которой направлено вдоль антенны (см. § 2 и 4). Поляризация излучения в этих двух системах будет различной: электрическому вектору в одной системе будет соответствовать магнитный вектор в другой. Таким путем можно рассчитать антенную решетку типа волновода со щелями на его боковых сторонах 
Принцип Бабине
Принцип Бабине (также теорема Бабине ) является предложением оптики и утверждает, что дифракционные изображения двух взаимодополняющих диафрагм ( например, щелевой диафрагмы и проволоки одинаковой толщины) находятся за пределами области, на которую попадает геометрическо-оптическое изображение (т. Е. рисунок без дифракционных эффектов), то же самое. Например, дифракционная картина отдельной щели практически не отличается от дифракционной картины от проволоки, а дифракционная картина круглого диска не отличается от дифракционной картины по размеру круга.
Название восходит к французскому физику Жаку Бабине (1794–1872), который сформулировал теорему в 1837 году.
Оглавление
Объяснение и применение
Принцип, установленный Бабине в 1837 году, теперь гласит, что взаимно дополняющие апертуры, то есть апертуры, в которых отверстия и непрозрачные области меняются местами, создают одинаковые дифракционные явления за пределами области, которую занимало бы геометрическо-оптическое изображение.
Применение в электродинамике
По аналогии с оптикой, принцип Бабине можно использовать и в электродинамике, так что получаются полезные соотношения. Например, электромагнитные эффекты могут быть рассчитаны через отверстия в проводящих плоскостях. Знания касательных к поверхности электрических полей достаточно для расчета полей, прошедших через отверстие. Например, его можно использовать для определения электромагнитного поля отверстия на бесконечно протяженной проводящей поверхности, в которой невозможно рассчитать распределение тока. По принципу Бабине отверстие становится проводящей поверхностью. В этом случае поверхностные токи должны быть рассчитаны только по отверстию, и обратное преобразование, наконец, дает результат для отверстия на бесконечно большой проводящей поверхности.
Вывод
Однако и точечное отверстие, и непрозрачное препятствие естественным образом создают дифракционную картину. Для этих дифракционных картин от точечного отверстия и препятствия амплитуда, падающая на экран, может быть разбита на геометрическую и дифракционную составляющие:
(3) Э. отверстие ( Икс ) + Э. задняя ( Икс ) знак равно Э. 0 ( Икс ) <\ displaystyle E _ <\ text 
(4) Э. Лохгео ( Икс ) + Э. индеец ( Икс ) знак равно Э. 0 ( Икс ) <\ displaystyle E _ <\ text
Если теперь установить уравнение. (1) и (2) в уравнении. (3) получаем:
(5) Э. отверстие ( Икс ) + Э. задняя ( Икс ) знак равно Э. Лохгео ( Икс ) + Э. изгиб отверстий ( Икс ) + Э. индеец ( Икс ) + Э. задница ( Икс ) знак равно Э. 0 ( Икс ) <\ displaystyle E _ <\ text
С формулой. (4) приводит к:
Фраунгофера дифракция
Расширение до размеров векторного поля
Описанные выше дифракционные явления относятся к величине электрических полей или распределению интенсивности дифрагированного электромагнитного излучения. Они получены (как и выше) в рамках приближений дифракционного интеграла Кирхгофа для размеров скалярного поля. Если кто-то хочет сделать выводы о комплексных электрических и магнитных полях и свойствах поляризации, он обычно ограничивается случаем диафрагм, сделанных из бесконечно тонких и идеально электропроводящих материалов. В случае, если компоненты электрического и магнитного поля падают перпендикулярно диафрагмам, следует отметить, что при переключении между дополнительными диафрагмами векторы поля должны быть повернуты на 90 ° вокруг нормали к поверхности. Для получения информации о направлении вращения и других подробностях см. Данные ссылки и учебник « Классическая электродинамика » Дж. Д. Джексона. Электрические дипольные моменты одной диафрагмы становятся магнитными дипольными моментами дополнительной диафрагмы и наоборот.
Принцип Бабине
Принцип (теорема) Бабине
Принцип (теорема) Бабине о свойствах дополнительных экранов является следствием гипотезы Френеля.
Выше названные экраны называют дополнительными, если выполняется условие:
Примером дополнительных экранов могут служить два экрана, имеющих отверстия, если отверстия на одном экране совпадают с непрозрачными участками второго экрана.
При суммировании выражений (3) и (4) получаем:
Выражение (6) принцип Бабине в скалярном виде.
Рассмотри дифракцию Фраунгофера. Пусть на пути распространения параллельных лучей отсутствуют любые препятствия, тогда световое поле в фокальной плоскости линзы будет равно нулю всюду, за исключением фокуса. В таком случае по теореме Бабине (6) мы получим в каждой точке рассматриваемой плоскости (не в фокусе линзы) равенство:
Равенство (8) означает, что картины дифракции при рассматриваемом явлении в фокальной плоскости линзы всюду одинаковые, исключением является фокус.
Теорема Бабине не является строгим утверждением, но ее нарушения являются существенными только у границ, рядом с которыми происходит дифракция. Представленная формулировка теоремы не всегда является удовлетворительной, так как она относится к скалярным полям и основана на приближении Кирхгофа.
Примеры задач с решением
Решение. Следуя условиям задачи и согласно принципу Бабине можно записать следующие соотношения между полями, приведенными в условиях:
Данные соотношения являются векторным аналогом скалярного принципа Бабине. Для плоской волны, которая падает на дифракционный экран, получаем, что в направлениях, которые не совпадают с направлениями падения волны, интенсивности поля дифракции для экрана и его дополнений одинаковы. При этом сами поля связывают соотношения:
Задание. Приведите пример, в котором следует использовать строгую векторную формулировку принципа Бабине.