Нечетная функция такова что 0 принадлежит d f

Четные и нечетные функции

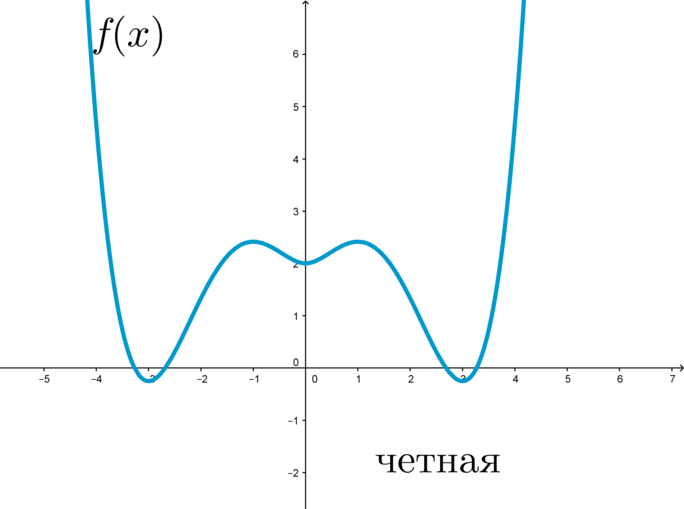
График четной функции симметричен относительно оси \(y\) :

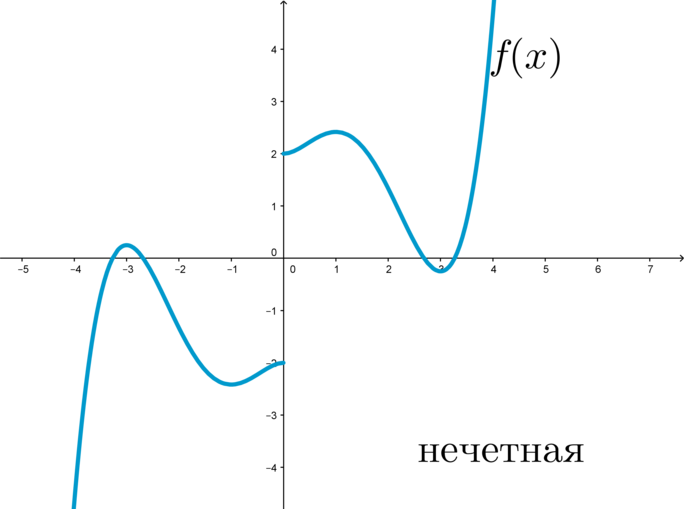
График нечетной функции симметричен относительно начала координат:

\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.

\(\blacktriangleright\) Некоторые свойства:

1) Произведение и частное двух функций одинаковой четности — четная функция.

2) Произведение и частное двух функций разной четности — нечетная функция.

3) Сумма и разность четных функций — четная функция.

4) Сумма и разность нечетных функций — нечетная функция.

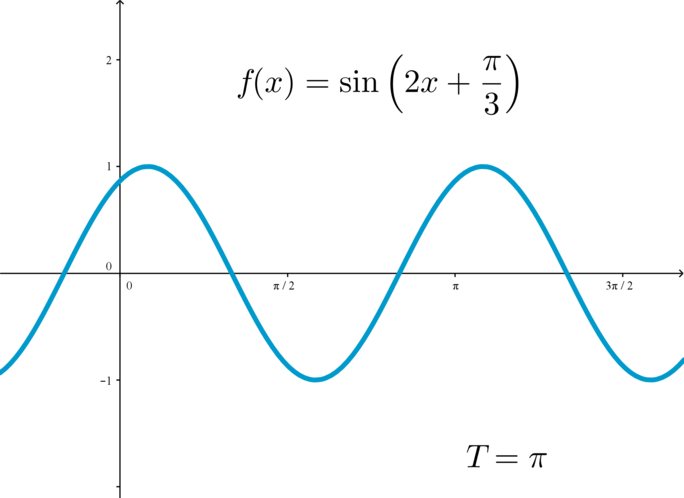
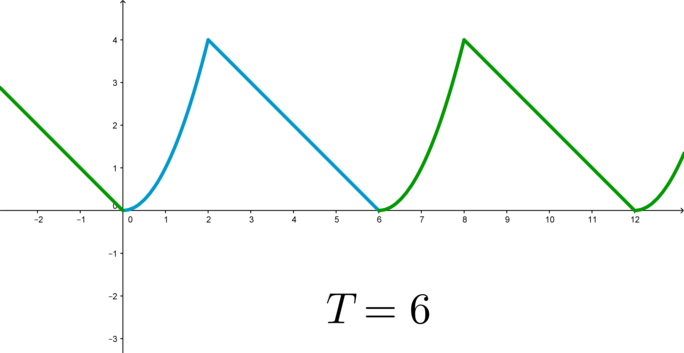
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:

При каких значениях параметра \(a\) уравнение

имеет единственное решение?

\[2\cdot 0+a\mathrm\,(\cos 0)+a^2=0 \quad \Rightarrow \quad a^2+a\mathrm\,1=0 \quad \Rightarrow \quad \left[ \begin\begin &a=0\\ &a=-\mathrm\,1 \end \end\right.\]

симметричен относительно начала координат.

Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)

\(\dfrac n2, n\in\mathbb\)

(Задача от подписчиков)

имеет хотя бы один корень.

(Задача от подписчиков)

имеет шесть различных решений.

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]

2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin 12-a>0\\-(a-10)>0\end\quad\Leftrightarrow\quad a

Источник

Нечетная функция имеет 4 нуля. Четность и нечетность функций

Способы задания функции

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Четная и нечетная функция

Исследуем на четность нижеприведенную функцию:

Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.

Периодическая функция

f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty)

Промежутки, где функция отрицательная, то есть f(x) (-\infty; x_<1>) \cup (x_<2>; x_<3>)

Ограниченность функции

Возрастающая и убывающая функция

Точкой максимума функции y=f(x) принято называть такую точку x=x_ <0>, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_ <0>), и для них тогда будет выполняется неравенство f(x)

Источник

Функция f(X) называется четной, если для каждого Х из области определения Df функции f(X) выполняется равенство f(-X) = f(X)

Главная > Документ

Четность, нечетность, периодичность функции

Функция f ( x ) называется четной, если для каждого х из области определения D f функции f ( x ) выполняется равенство f (- x ) = f ( x );

Из равенств f (- x )= f ( x ) или f (- x )=- f ( x ) следует:

Значения функции f ( x ) в симметричных точках совпадают или противоположны.

Понятия четной или нечетной функции можно вводить, и исходя из геометрических представлений о симметрии:

функция f ( x ), график которой симметричен относительно оси ординат, называется четной;

функция f ( x ), график которой симметричен относительно начала координат, называется нечетной.

При ответе на вопрос данной темы очень полезно иметь перед глазами картинку, изображающую схематично график функции. Задание может быть так же на вычисление значения четной или нечетной функции по какому-то уже известному значению.

Сформулируйте правила для определения четности (нечетности) различных функций ; композиций двух функций: а) четных; б) нечетных; в) четной и нечетной. Приведите примеры, иллюстрирующие правила.

На приведенных рисунках (из части А вариантов ЕГЭ) найдите четные и нечетные функции.

Нарисуйте график функции, заданной на множестве неотрицательных чисел, достройте его так, чтобы получился график функции: четной, нечетной, общего вида; сделайте это упражнение для множества неположительных чисел.

Исследуйте функцию на четность нечетность:

а) ƒ( х ) = х 3 – sin х; б) ƒ( х ) = х 5 tg х.

Так как ƒ(– х ) = – ƒ( х )  ƒ( х ) = х 3 – sin х является нечетной.

б) ƒ(- х ) = (- х ) 5 tg (- х ) =- х 5 (-tg х ) = х 5 tg х

ƒ(- х ) = ƒ( х )= > ƒ( х ) = х 5 tg х является четной.

Найдите f(-x) для следующих функций:

.

Найдите значение функции у=3f (-x)-g(-x)f(x) в точке х 0 0, если известно, что функция у=f(x)-четная, а у=g(x)-нечетная; f(x 0 )=1, g(x 0 )=3.

Функция у=f(x), определена на R, нечетная, f(x)=g(x),где

g(x)=x(2x+1)(x-3)(x+2). Найти значение h(-1), если

Параметры а и b таковы, что функция — нечетная, — четная. Найдите значение выражения af(-2)+bg(-2).

Решение : 1. D(f)=R, симметричное множество, и f(-x)=- f(x) по условию

и т.к. f(-x)=- f(x), то

=

=

 а=3  . Итак, f(x)=x 3

2. D(g)=R, симметричное множество, и g(-x)= g(x) по условию

=

Значения а и b таковы, что f(x)= нечетная, g(x)= четная. Найти af 2 (-5)+bg(-5)

При х0, f (x)+g (x)=2 (x 2 +8x)=18, х 2 +8х-9=0, х 1 =-9, х 2 =1- не удовлетворяет условию х0. Т. е. при х0 уравнение f (x)+g (x)=18 имеет один корень, х=-9.

Решение. У четной функции корни симметричны относительно точки 0. Найдем положительные корни уравнения g(x)=0. Это единственный корень х 1 =х 2 =--корень уравнения f(x)=0. х 0 =0- корень g(x)=0 х 0 =0 –корень f(x)=0.

y=f(x) четная функция и определена на -6;6. Для неотрицательных чисел f(x)=g(x), где g(x)= (х+2)(х-1)(х-2)(2х-13). Сколько корней имеет уравнение f(x)=0?

Решение: Найдем количество корней на 0;6. Так как функция четная, т.е. её график симметричен относительно оси Оу, то столько же корней и на -6;0. Если х0;6, то f(x)=g(x), а значит (х+2)(х-1)(х-2)(2х-13)=0

х=-2, х=1, х=2, х ==6,5. Итак, если х0;6, то два корня, следовательно на -6;0 тоже два корня.

Для четной функции f(x) и нечетной функции g(x) для всех действительных значений аргумента выполнено равенство f(x)+g(x)=x 2 +3x-2. Найдите значение выражения f(2)-4g(3).

Четная функция y=f(x) определена на всей числовой прямой. Её график на отрезке [2;5] совпадает с графиком функции y=g(x). Вычислите

Четная функция y=f(x) и нечетная функция y=g(x) определены на всей числовой прямой. Для функции h(x)=8 x +f(x)sinx-g(x) вычислите сумму h(-1)+h(0)+h(1).

Решение: h(x)=8 x +f(x)sinx-g(x)

Так как y= f(x) четная функция, то f(-x)= f(x).

Так как y=g(x) нечетная функция, то g(-x)=- g(x)

h(-1)=+f(-1)sin(-1)-g(-1)= — f(1)sin1+g(1)

h(0)=8 0 + f(0) sin0-g(0)=1+0-0=1, т.к. g(x)- нечетная, то g(0)=0

h(-1)+h(0)+h(1)= — f(1)sin1+g(1)+1+8+f(1)sin1-g(1)= +1+8=

Ответ:

При каких значениях параметра a функция является четной.

Решение. 1-й случай. Предположим, что при всех значениях аргумента хR. 2 х +а≠0. В этом случае данная функция определена на всей числовой прямой и при всех значениях х f(x) + f(-x) = 0. В частности, должно выполняться равенство f(0) = 0,то есть =0. Отсюда находим единственное возможное значение: а =-3.

Рассмотрим теперь функ­цию f(x) = . При , f(x). Если же , то .

Следовательно, эта функция не является нечетной.

2-й случай. Пусть при некоторых значениях аргу­мента знаменатель обращается в нуль. Такое значе­ние — единственное и равно log 2 (—а). Область опре­деления нечетной функции симметрична относитель­но точки х (х= 0). Следовательно, знаменатель может равняться нулю только при х = 0. Отсюда находим единственное возможное значение параметра: а =- 1.

В результате приходим к функции f(x). Эта функция является нечетной:

.

Найдите все значения параметра а при которых функция

f(x)= (a-1)x 2 +(a 2 +2a-3)x+1 является четной функцией.

Решение: D(f x )=R, т.е. область определения симметрична относительно 0, а значит для любого х выполняется условие f(-x)=f(x)/

Докажем, что при этих а нет других корней.

Если а=0, то х 2 =0 или х=0, и это единственный корень

х 2 +4sin 2 1=4 sin1sin(cosх) (*)

Оценим левую и правую часть:

х 2 +4sin 2 1 4sin 2 1

-1 cosx  1, на -1;1 функция возрастает, тогда наибольшее значение функция достигает когда cosx=1, т.е 4 sin1sin(cosх) 4 sin1sin1= 4sin 2 1.

Итак, условие (*) выполняется, если левая и правая части равны 4sin 2 1

это верно.

Ответ: а = 0, а = 2sin1

х=0, х=1,х=-1, т.е. три корня.

Ответ:

Если Т>0 период функции f(x), то и nT- тоже период, nZ

Если Т>0 период функции f(x), то функция f(kx+b) имеет период . Если Т 0 – основной период f(x), то основной период функции f(kx+b)

Если Т 1 >0 основной период f(x), Т 2 >0 основной период g(x), и является рациональным числом (mZ, nN), то для любой комбинации kf(x)+ pg(x) основным периодом является Т=НОК(Т 1 ; Т 2 )

Периодическая функция не может иметь конечное число разрывов, их бесконечно много

Если х 0 D(f(x)) периодической функции, то x 0 +nT (nZ) тоже принадлежит D(f(x)).

Периодическая функция каждое свое значение принимает в бесконечном числе точек.

На предложенных рисунках найдите периодические функции, определите основной период.

а) f(1) и f(31); б) f(11) и f(110); в) f(-17) и f(831); г) f(6+) и f(-6).

Функция у= f(x) – периодическая, с периодом Т=2. Известно, что

f(0)=-5. Вычислите: f(2), f(-22), f(12k+8), f(4-8k), где k – некоторое целое число.

Функция у= f(x) – периодическая, с периодом Т=3. Известно, что

f(5)=1, f(-8)=3, а на отрезке [1;2] эта функция совпадает с y=ax+b.

На отрезке [1;2] f(x) =ax+b, тогда или , тогда

Функция y=f(x) c T=4 на (-1;3] совпадает с функцией y=x-a . Известно, что f(-7)=3, f(10)=2. Найти f(13,5).

На (-1;3] y=f(x) совпадает с функцией y=x-a .

или или Итак, а=4, получим функцию y=x-4.

Источник