Нечетная функция имеет 4 нуля докажите что 0 не принадлежит d f

Нечетная функция имеет 4 нуля. Четность и нечетность функций

Способы задания функции

x	−2	−1	0	1	2	3
y	−4	−3	−2	−1	0	1

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Четная и нечетная функция

Исследуем на четность нижеприведенную функцию:

Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.

Периодическая функция

f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty)

Промежутки, где функция отрицательная, то есть f(x) (-\infty; x_<1>) \cup (x_<2>; x_<3>)

Ограниченность функции

Возрастающая и убывающая функция

Точкой максимума функции y=f(x) принято называть такую точку x=x_ <0>, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_ <0>), и для них тогда будет выполняется неравенство f(x)

Источник

Нечетная функция имеет 4 нуля. Четность и нечетность функций

Читайте также

Способы задания функции

x	−2	−1	0	1	2	3
y	−4	−3	−2	−1	0	1

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Четная и нечетная функция

Исследуем на четность нижеприведенную функцию:

Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.

Периодическая функция

f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty)

Промежутки, где функция отрицательная, то есть f(x) (-\infty; x_<1>) \cup (x_<2>; x_<3>)

Ограниченность функции

Возрастающая и убывающая функция

Точкой максимума функции y=f(x) принято называть такую точку x=x_ <0>, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_ <0>), и для них тогда будет выполняется неравенство f(x) 0 при х > 0,4 ; f (х ) –1

– Выполняя данную работу, ребята мы выявили ещё одно свойство функции, незнакомое вам, но не менее важное, чем остальные – это чётность и нечетность функции. Запишите тему урока: «Чётные и нечётные функции», наша задача – научиться определять чётность и нечётность функции, выяснить значимость этого свойства в исследовании функций и построении графиков.
Итак, найдём определения в учебнике и прочитаем (стр. 110). Слайд

Изучение вопроса о том, является ли функция чётной или нечётной называют исследованием функции на чётность. Слайд

Опр 3. Если числовое множество вместе с каждым своим элементом х содержит и противоположный элемент –х, то множество Х называют симметричным множеством.

– У чётных функций область определения – симметричное множество? У нечётных?
– Если же D(f ) – несимметричное множество, то функция какая?
– Таким образом, если функция у = f (х ) – чётная или нечётная, то её область определения D(f ) – симметричное множество. А верно ли обратное утверждение, если область определения функции симметричное множество, то она чётна, либо нечётна?
– Значит наличие симметричного множества области определения – это необходимое условие, но недостаточное.
– Так как же исследовать функцию на четность? Давайте попробуем составить алгоритм.

Алгоритм исследования функции на чётность

1. Установить, симметрична ли область определения функции. Если нет, то функция не является ни чётной, ни нечётной. Если да, то перейти к шагу 2 алгоритма.

2. Составить выражение для f (– х ).

1) D(h) = (–∞; 0) U (0; +∞), симметричное множество.

2) h (– х) = (–х) 5 + – х5 –= – (х 5 +),

3) h(– х) = – h (х) => функция h(х) = х 5 + нечётная.

у = f (х ), D(f) = (–∞; –9)? (–9; +∞), несимметричное множество, значит функция ни чётная, ни нечётная.

а); б) у = х· (5 – х 2).2. Исследуйте на чётность функцию:

а) у = х 2 · (2х – х 3), б) у =

3. На рис. построен график у = f (х ), для всех х, удовлетворяющих условию х? 0.
Постройте график функции у = f (х ), если у = f (х ) – нечётная функция.

Взаимопроверка по слайду.

6. Задание на дом: №11.11, 11.21,11.22;

Доказательство геометрического смысла свойства чётности.

***(Задание варианта ЕГЭ).

1. Нечётная функция у = f(х) определена на всей числовой прямой. Для всякого неотрицательного значения переменной х значение этой функции совпадает со значением функции g(х ) = х (х + 1)(х + 3)(х – 7). Найдите значение функции h(х ) = при х = 3.

7. Подведение итогов

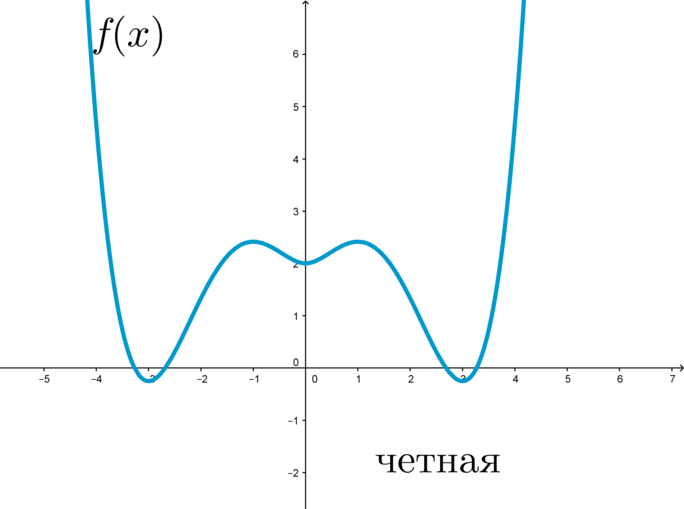
График четной функции симметричен относительно оси \(y\) :

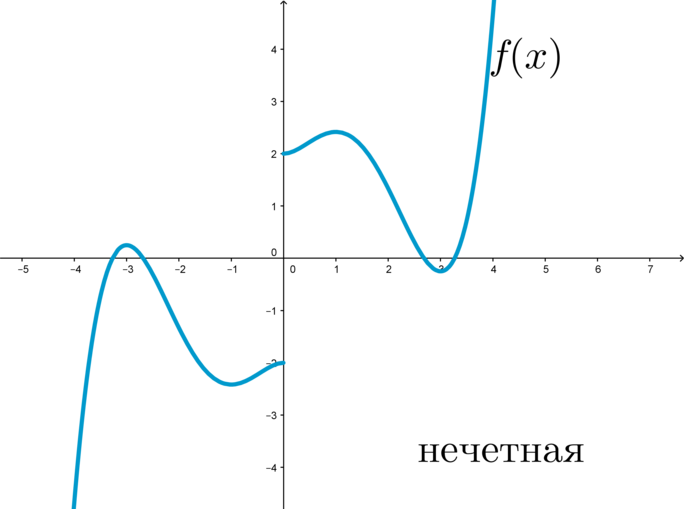
График нечетной функции симметричен относительно начала координат:

\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.

\(\blacktriangleright\) Некоторые свойства:

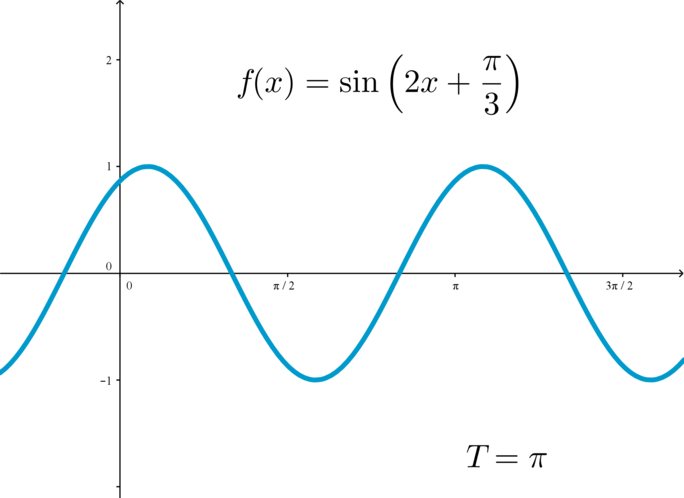
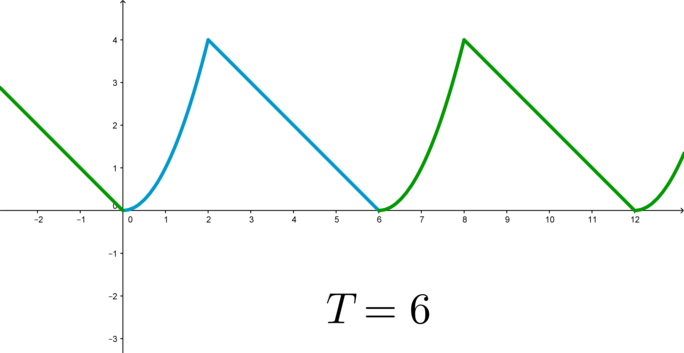
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:

Пример: у функции \(f(x)=\sqrt x+1\) область определения: \(x\in

Уровень задания: Равен ЕГЭ

При каких значениях параметра \(a\) уравнение

имеет единственное решение?

Уровень задания: Равен ЕГЭ

симметричен относительно начала координат.

Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)

\(\dfrac n2, n\in\mathbb\)

Уровень задания: Равен ЕГЭ

(Задача от подписчиков)

Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график \(g(x)=|a+2|\cdot \sqrtx\) проходил через точку \(A\) :

2) Пусть \(a \[\dfrac<64>9a=|a+2|\cdot \sqrt <-8>\quad\Leftrightarrow\quad \left[\begin\begin &a=\dfrac<18><23>\\ &a=-\dfrac<18> <41>\end \end\right.\] Так как \(a

Уровень задания: Равен ЕГЭ

имеет хотя бы один корень.

(Задача от подписчиков)

Уровень задания: Равен ЕГЭ

имеет шесть различных решений.

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \

имело четыре различных корня, отличных от нуля, представляющих вместе с \(x=0\) арифметическую прогрессию.

Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций \(f\) и \(g\) имели хотя бы одну точку пересечения. Следовательно, нужно: \ Решая данную совокупность систем, получим ответ: \\]

Источник

Четные и нечетные функции

График четной функции симметричен относительно оси \(y\) :

График нечетной функции симметричен относительно начала координат:

\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.

\(\blacktriangleright\) Некоторые свойства:

1) Произведение и частное двух функций одинаковой четности — четная функция.

2) Произведение и частное двух функций разной четности — нечетная функция.

3) Сумма и разность четных функций — четная функция.

4) Сумма и разность нечетных функций — нечетная функция.

Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:

При каких значениях параметра \(a\) уравнение

имеет единственное решение?

\[2\cdot 0+a\mathrm\,(\cos 0)+a^2=0 \quad \Rightarrow \quad a^2+a\mathrm\,1=0 \quad \Rightarrow \quad \left[ \begin\begin &a=0\\ &a=-\mathrm\,1 \end \end\right.\]

симметричен относительно начала координат.

Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)

\(\dfrac n2, n\in\mathbb\)

(Задача от подписчиков)

имеет хотя бы один корень.

(Задача от подписчиков)

имеет шесть различных решений.

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]

2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin 12-a>0\\-(a-10)>0\end\quad\Leftrightarrow\quad a

Источник