Нечетная функция f такова что 0 принадлежит d f найдите f 0
Четные и нечетные функции
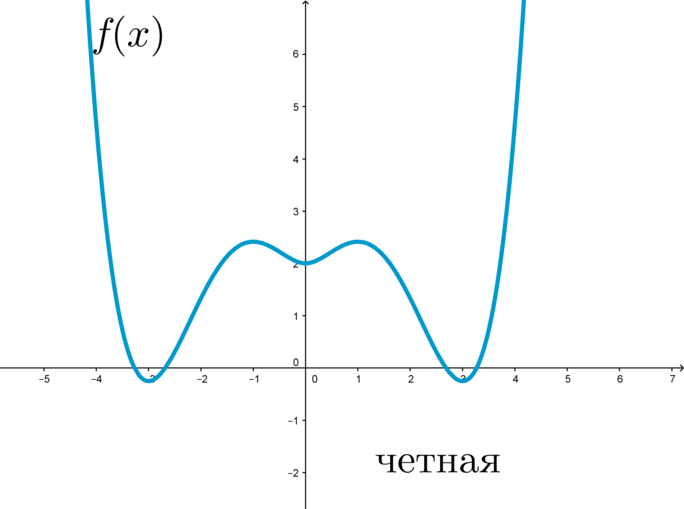
График четной функции симметричен относительно оси \(y\) :
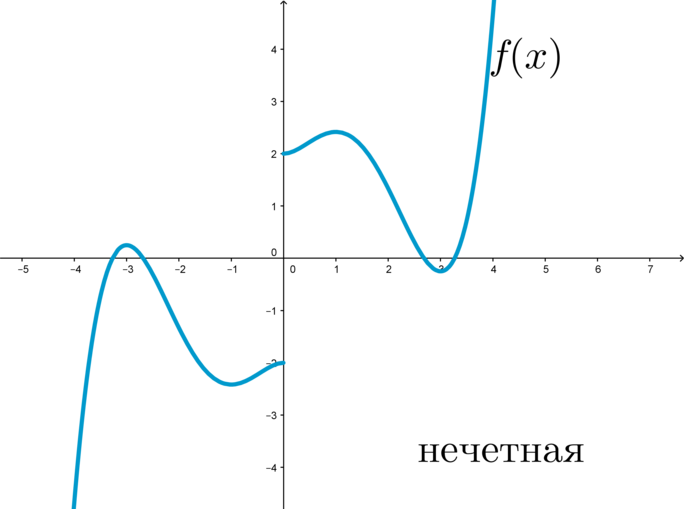
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
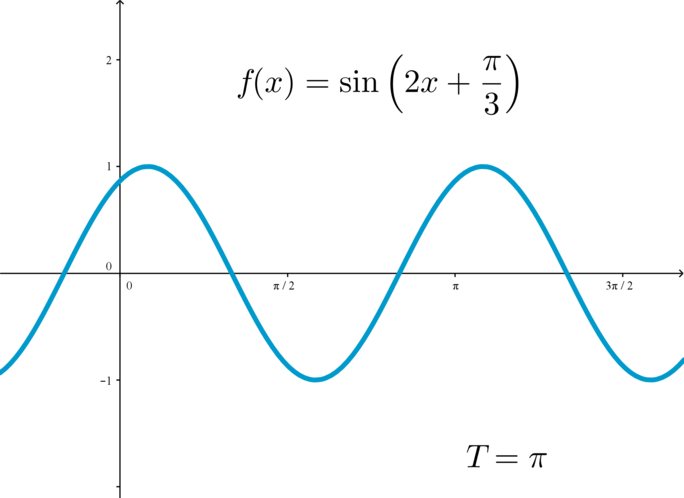
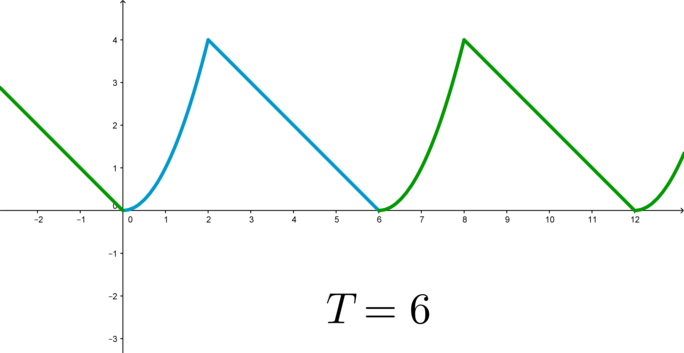
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
\[2\cdot 0+a\mathrm
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
(Задача от подписчиков)
имеет хотя бы один корень.
(Задача от подписчиков)
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin
Презентация «Анализ графиков (новое 9 задание). Подготовка к профильному ЕГЭ по математике»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Описание слайда:
Добрый день, уважаемые коллеги! Приятно видеть вас в этой аудитории, и очень надеюсь, что сегодня у нас с вами получится интересное и полезное мероприятие.
Описание слайда:
Мастер-класс
учителя математики
МОУ «СОШ№ 14»
Рискуловой Тотайхан Оразалиевны
по теме:
«Анализ графиков (новое 9 задание). Подготовка к профильному ЕГЭ по математике»
а Эдельбай
Благодарненский район
Описание слайда:
«Расскажи мне и я забуду. Покажи мне и я пойму. Позволь мне сделать самому, и я научусь»
Конфуций
Конфуций-древнекитайский проповедник,
писатель, философ.
Описание слайда:
Описание слайда:
Цель мастер-класса:
показать приемы решения нового 9 задания по теме «Анализ графиков»
развивать логическое мышление, память, познавательный интерес
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
7
9 задание. На рисунке изображены графики функций f(x)=5х+9 и g(x)= ах²+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки B
Описание слайда:
Описание слайда:
Решение.
|bx+c|=0 в точке излома. Значит, bx+c=0 при х=2.
9 задание
На рисунке изображен график функции вида 𝒇 𝒙 = 𝒂 x+|bx+c|+d, где числа 𝒂,b, c и d-целые.
Найдите корень уравнения bx+c=0
Описание слайда:
9 задание.
На рисунке изображён график функции вида f(x)=ax + |bx + c| +d, где числа a, b, c и d — целые. Найдите корень уравнения ax + d=0.
Описание слайда:
Описание слайда:
Описание слайда:
9 задание. На рисунке изображен график функции f(x)= 𝒌 𝒙 +a. Найдите f (0,25)
Описание слайда:
Описание слайда:
Описание слайда:
График функции имеет горизонтальную асимптоту y=2,
значит, k=2.
Ответ:2
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
1.ПРОЕКТ. Демонстрационный вариант
контрольных измерительных материалов
единого государственного экзамена 2022 года
по МАТЕМАТИКЕ. Профильный уровень. ФИПИ
2.Статград. Новое ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
3.Образовательный портал «СДАМ ГИА» Математика профильного уровня.
Описание слайда:
Хорошие результаты ЕГЭ и ОГЭ по математике позволяют выпускникам школы успешно решить свои жизненные планы.
Описание слайда:
Описание слайда:
Мастер-класс был актуальным, полезным, интересным
Ничего нового на мастер- классе я для себя не узнал
Нарисуйте пятиугольгик или треугольник
Описание слайда:
Описание слайда:
Описание слайда:
Спасибо вам за то, что вы есть…
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Памятка для учащихся «Целые числа»
Пробный экзаменационный вариант «ЕГЭ математика профиль пробник 2 вариант» (2022)
Статья» Формирование универсальных учебных действий на уроках математики»
3 класс Школа России Для детей с программой ОВЗ 7.2 Данная разработка поможет ориентироваться в заданиях, правильно сформулировать задание и выполнить его. Банк заданий для промежуточной аттестации по математике 3 класс
Конспект по математике: «Решение задач»
Конспект по математике:Закрепление по теме «Сложение и вычитание. Свойства сложения»
Презентация к уроку «Натуральные числа»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5375312 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Учителям истории предлагают предоставить право бесплатно посещать музеи
Время чтения: 2 минуты
Во Франции планируют ввести уголовное наказание за буллинг в школе
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Международный конгресс-выставка «Молодые профессионалы» пройдет с 12 по 14 декабря в Москве
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Нечетная функция f такова что 0 принадлежит d f найдите f 0
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = 2 × F(n − 2), если n> 1 и при этом n — нечётно.
Чему равно значение функции F(26)?
Приведём программу на Паскале, решающий данную задачу:
Приведём аналитическое решение. Заметим, что значения функции от нечётных n являются значениями степеней двойки: F(1) = 1, F(3) = 2, F(5) = 4 и т. д. Значит, F(25) = 4096. Тогда F(26) = 26 + 4096 = 4122.
Алгоритм вычисления значения функции F(n), где n — целое неотрицательное число, задан следующими соотношениями:
F(n) = n / 2 + F(n − 1) + 2, если n > 1 и при этом чётно.
Чему равно значение функции F(49)? В ответе запишите только целое число.
Приведём решение задачи на четырёх языках программирования:
function F(N: integer): integer;
using namespace std;
if(n 1 и mod(n,2)=1 : знач:=F(n-1)+3*n*n
при n>1 и mod(n,2)=0 : знач:=div(n,2)+F(n-1)+2
Результат работы программ — 62820.
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = 2 × F(n − 2), если n > 1 и при этом n нечётно.
Чему равно значение функции F(26)?
Приведём решение задачи на четырёх языках программирования:
function F(N: integer): integer;
else if n mod 2 = 0 then F := n + F(n-1)
using namespace std;
if(n % 2 == 0) return n + F(n-1);
Результат работы программ — 4122.
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
Чему равно значение функции F(30)? В ответе запишите только натуральное число.
Преобразуем выражение для F(n):
Это выражение для суммы арифметической прогрессии с первым членом 1 и разностью 1. Таким образом, Откуда
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
Чему равно значение функции F(40)? В ответе запишите только натуральное число.
Преобразуем выражение для F(n):
Это выражение для суммы арифметической прогрессии с первым членом 1 и разностью 1. Таким образом, Откуда