стейт машина что это
Конечный автомат (он же машина состояний) на чистом С
Почти каждый микроконтроллерщик сталкивался с громадными switch-case и мучительно их отлаживал.
И много кто, начиная писать реализацию какого-либо протокола, задумывался как написать её красиво, изящно, так чтобы через месяц было понятно что ты имел в виду, чтобы она не отжирала всю память и вообще какала бабочками.
И вот тут на помощь приходят машины состояний, они же конечные автоматы (те самые которые используются в регулярных выражениях).
Собственно через регулярные выражения я к ним и пришёл.
Недавно мне потребовалось реализовать несложную функциональность устройства с 4-мя кнопками — выделение в потенциально хаотичных нажатиях кнопок двух кодовых последовательностей и выполнение определённых действий, когда последовательность найдена.
Поясню на примере: есть 4 кнопки — A, B, C, D и кодовая последовательность ACDA. Тогда при последовательном нажатии B, C, A, D, A, C, D, A, B, устройство должно зажечь лампочку после 8-го (предпоследнего) нажатия. С точки зрения регулярных выражений задача проста — ищем во входной строке подстроку «ACDA». Как только нашли — зажигаем лампочку. Но тащить в микроконтроллер какую-нибудь библиотеку по работе с regexp не хотелось. Я чувствовал что всё можно сделать самому и проще. Тогда я решил попробовать самостоятельно реализовать конечный автомат соответствующий поиску данной подпоследовательности.
А теперь — немного теории и практики:
Основная черта конечных автоматов — они описываются набором возможных состояний, набором сигналов (событий) и таблицей переходов. Таблица переходов — это сопоставление паре из текущего состояния и пришедшего сигнала нового состояния.
Представим, что у нас есть автомат с 3 состояниями и 3 сигналами, которые нужно обрабатывать. По приходу каждого сигнала автомат совершает переходит в новое состояние.
Очевидно что данный код не очень удобочитаем и будет катастрофически разрастаться с увеличением количества состояний и сигналов.
Кроме того, если мы захотим в каждый переход добавить какое-либо однотипное действие (например логирование — что-то вроде ), то это породит кучу изменений в коде. При редактировании таких изменений почти наверняка будет допущена какая-нибудь ошибка и отладка превратится в ад.
Заметим, что суть двух вложенных switch — это выбор из таблицы (по колонке и по столбцу) и вспомним что формально конечные автоматы удобно записывать в виде таблицы переходов где каждая строка соответствует сигналу, каждый столбец — состоянию, а на пересечении записано состояние в которое переходит автомат.
Попробуем упростить имеющийся код, задав таблицу переходов, извините за тафтологию, таблицей.
Продемонстрированый вид инициализации даннных известен как designated inits и был введён в С99.
теперь надо полученную структуру данных обработать — пишем функцию doFSM_table:
Чтобы сделать получившийся автомат ещё более универсальным и придать ему возможность совершать какие-то действия кроме перехода по состояниям добавим в таблицу указатели на функции-обработчики, соответствующие переходам:
Вообще улучшать данный механизм можно долго, но данная статья ставит своей целью не разработать универсальную библиотеку для реализации конечных автоматов, а продемонстрировать как некоторые задачи могут быть решены значительно проще и компактнее чем «в лоб», при этом не прибегая ни к каким замысловатым библиотекам или языкам.
В заключение приведу таблицу, получившуюся для задача поиска подпоследовательности, с которой я начинал:
Простые стейт-машины на службе у разработчика
Представьте на минутку обычного программиста. Допустим, его зовут Вася и ему нужно сделать анимированную менюшку на сайт/десктоп приложение/мобильный апп. Знаете, которые выезжают сверху вниз, как меню у окна Windows или меню с яблочком у OS X. Вот такое.
Начинает он с одного выпадающего окошка, тестирует анимацию, выставляет ease out 100% и наслаждается полученным результатом. Но вскоре он понимает, что для того, чтобы управлять менюшкой, хорошо бы знать закрыто оно сейчас или нет. Мы-то с вами тут программисты опытные, все понимаем, что нужно добавить флаг. Не вопрос, флаг есть.
Вроде, работает. Но, если быстро кликать по кнопке, меню начинает моргать, открываясь и закрываясь не успев доанимироваться в конечное состояние. Вася добавляет флаг animating. Теперь код у нас такой:
Через какое-то время Васе говорят, что меню может быть полностью выключено и неактивно. Не вопрос! Мы-то с вами тут программисты опытные, все понимаем, что… нужно добавить ЕЩЕ ОДИН ФЛАГ! И, всего-то через пару дней разработки, код меню уже пестрит двустрочными IF-ами типа вот такого:
Вася начинает задаваться вопросами: как вообще может быть, что animating == true и enabled == false; почему у него время от времени все глючит; как тут вообще поймешь в каком состоянии находится меню. Ага! Состояния. О них дальше и пойдет речь.
Знакомьтесь, это Вася.
Состояние
Вася уже начинает понимать, что многие комбинации флагов не имеют смысла, а остальные можно легко описать парой слов, например: Disabled, Idle, Animating, Opened. Все мы тут программисты опытные, сразу вспоминаем про state machines. Но, для Васи придется рассказать что это и зачем. Простым языком, без всяких математических терминов.
У нас есть объект, например, вышеупомянутая менюшка. Объект всегда находится в каком-то одном состоянии и реагируя на различные события может между этими состояниями переходить. Обычно состояния, события и переходы удобно описывать вот такими схемами (кружочками обозначены начальное и конечные состояния):
Из схемы понятно, что из состояния Inactive в Active можно попасть только по событию Begin, а из состояния Paused можно попасть как и в Active, так и в Inactive. Такую простую концепцию почему-то называют «Конечный Автомат» или «Finite State Machine», что очень пугает обычных людей.
По завету ООП, состояния должны быть скрыты внутри объекта и просто так снаружи не доступны. Например, у объекта во время работы может быть 20 разных состояний, но внешнее API на вопрос «чо как дела?» отвечает «ничо так» на 19 из них и только на 1 ругается матом, что проср*ли все полимеры.
Следуя концепции стейт машин, очень легко структурировать код так, что всегда будет ясно что и как делает тот или иной объект. Всегда будет понятно, что что-то пошло не так, если система вдруг попыталась перейти в недоступное из данного состояния состояние. А события, которые вдруг посмели прийти в неправильное время, можно смело игнорировать и не бояться, что что-нибудь сломается.
Самая простая в мире стейт машина
Допустим, теперь Вася делает проект на C# и ему нужна простая стейт машина для одного типа объектов. Он пишет что-то типа такого:
А вот так обрабатывает события в зависимости от текущего состояния:
Но, мы-то с вами тут программисты опытные, все понимаем, что метод setState в итоге разрастется на пару десятков страниц, что (как написано в учебниках) не есть хорошо.
State Pattern
Погуглив пару часов, Вася решает, что State Pattern идеально подходит в данной ситуации. Тем более, что старшие программисты все время соревнуются кто больше паттернов запихнет в свой апп, так что, решает Вася, паттерны это дело важное.
Например, для State Pattern можно сделать интерфейс IState:
И по отдельному классу для каждого состояния, которые этот интерфейс имплементят. В теории выглядит красиво и 100% по учебнику.
Но, во-первых, для каждой несчастной мелкой стейт машины нужно городить уйму классов, что само по себе небыстро. Во-вторых, рано или поздно начнутся проблемы с доступом к общим данным. Где их хранить? В основном классе? А как классы-состояния получат к ним доступ? А как мне тут за 15 минут перед дедлайном впилить быстро мелкий хак в обход правил? И подобные проблемы взаимодействия, которые будут сильно тормозить разработку.
Реализация на основе особенностей языка
Некоторые языки программирования облегчают решение тех или иных задач. В Ruby, например, так вообще есть целый DSL (и не один) для создания конечных автоматов. А в C# конечный автомат можно упростить через Reflection. Вот как-то так:
Реализовав систему описанную выше, Вася понимает, что у нее тоже больше минусов, чем плюсов:
Фреймворк
А тем временем, Вася уже вовсю стал вникать в теорию стейт машин и решил, что хорошо бы иметь возможность формально их описывать через API или (о Боже) через XML, что в теории звучит круто. Мы-то с вами тут программисты опытные, все понимаем, что нужно писать свой фреймворк. Потому что другие не подходят, так как у всех у них есть один фатальный недостаток.
Вася решил, что с помощью его фреймворка можно будет быстро и легко создать стейт машину без необходимости писать много ненужного кода. Фреймворк не будет накладывать никаких ограничений на разработчика. Все вокруг будут веселы и жизнерадостны.
Я попробовал множество фреймворков на разных языках, несколько подобных написал сам. И всегда для описания конечного автомата средствами фреймворка требовалось больше кода, чем в простом примере. Все они накладывают те или иные ограничения, а многие пытаются делать сразу столько всего, что для того, чтобы разобраться, как же тут все-таки создать несложную стейт машину, приходится продолжительное время рыться в документации.
Вот, например, описание конечного автомата фреймворком stateless:
Но, пробившись через создание стейт машины, можно воспользоваться полезными функциями, которые предоставляет фреймворк. В основном это: проверка правильности переходов, синхронизация зависимых стейт машин и суб-стейт машин и всяческая защита от дурака.
XML — это отдельное зло. Кто-то когда-то придумал использовать его для написания конфигов. Стадо леммингов java разработчиков длительное время молилось на него. А теперь никто уже и не знает зачем все используют XML, но продолжают бить всех, кто пытается от него избавиться.
Вася тоже загорелся идеей, что можно все сконфигурировать в XML и НЕ ПИСАТЬ НИ СТРОЧКИ КОДА! В итоге в его фреймворке отдельно лежат XML файлы примерно такого содержания:
Класс! И никакого программирования. Но, мы-то с вами тут программисты опытные, все понимаем, что программирование никуда не ушло. Вася заменил кусок императивного кода на кусок декларативного кода, добавив при этом во фреймворк интерпретатор XML, который все еще в пару раз усложнил. А потом попробуй это отдебажить, когда код на разных языках и разбросан по проекту.
Соглашение
И тут Васе все это надоело и он вернулся обратно к самому простому в мире конечному автомату. Он его немного переделал и придумал правила как писать в нем код.
UPDATE: спасибо за комментарии. Здесь действительно не хватало небольшого объяснения.
У нас есть несколько состояний. Переход между ними — это транзакция из атомарных операций, то есть они все происходят всегда вместе, в правильном порядке и между ними не может вклиниться еще какой-то код. При смене состояния с A на B происходит следующее: выполняется код выхода из состояния A, состояние меняется с A на B, выполняется код входа в состояние B.
Для перехода на состояние A нужно вызвать метод stateA, который выполнит нужную логику и вызовет setState(A). Самому вызывать setState(A) крайне не рекомендуется.
UPDATE: В setState() пишется уникальная логика выхода из состояния, а в stateB() возможна специфическая логика выхода из состояния A при переходе в B. Но очень редко используется.
Простое соглашение для написания стейт машин. Оно достаточно гибкое и имеет следующие плюсы:
Как и во всех соглашениях, какой-то код может сперва находиться в одном месте, но потом у него появится другой смысл, или окажется, что он где-то дублируется. Тогда мы можем его перенести в другое место. Никто нам не запрещает. Все-таки код не вытесан из камня, это всего лишь текст, который (о ужас!) можно и нужно менять с развитием проекта.
UPDATE: а setState() вполне можно заменить одним сеттером для наглядности.
Заключение
На этом заканчивается увлекательное приключение Васи в мире стейт машин. А ведь впереди еще столько всего интересного. Отдельного топика бы только заслужили параллельные и зависимые стейт машины.
Я надеюсь, что, если вы еще не используете стейт машины повсеместно, эта статья перетянет вас на сторону добра; если вы пишите свой уберфреймворк для работы со стейт машинами, она поможет свежим взглядом посмотреть на то, что у вас получается.
Я надеюсь, что эта статья поможет разработчикам задуматься где и когда стоит использовать паттерны и фреймворки, и что описанное соглашение по оформлению стейт машин окажется кому-то полезным.
Теория вычислений. Введение в конечные автоматы
Это до предела упрощенная модель компьютера имеющая конечное число состояний, которая жертвует всеми особенностями компьютеров такие как ОЗУ, постоянная память, устройства ввода-вывода и процессорными ядрами в обмен на простоту понимания, удобство рассуждения и легкость программной или аппаратной реализации.
С помощью КА можно реализовать такие вещи как, регулярные выражения, лексический анализатор, ИИ в играх и тд.
У конечных автоматов имеется таблица переходов, текущее состояние автомата, стартовое состояние и заключительное состояние.
Таблица переходов — В ней хранятся переходы для текущего состояния и входного символа. Простейшая реализация может быть как двумерный массив.
Здесь видно, что из состояния 0 в состояние 1 можно попасть только, если у нас будет входной символ ‘a’, из состояния 1 в состояние 2, если символ ‘b’.
Текущее состояние — множество состояний в котором автомат может находиться в данный момент времени.
Стартовое состояние — состояние откуда КА начинает свою работу.
Заключительное состояние — множество состояний в которых автомат принимает определенную цепочку символов, в ином случае отвергает.
Детерминированные конечные автоматы (deterministic finite automaton)
Простейший КА, в котором может быть одно состояние в текущий момент времени, обладает детерминированностью.
Детерминированность — для всех состояний имеется максимум и минимум одно правило для любого возможного входного символа, то есть например, для состояния 1 не может быть два перехода с одним и тем же входным символом.
Недетерминированные конечные автоматы (nondeterministic finite automaton)
НКА не является каким-то существенным улучшением ДКА, просто в нем добавлен так сказать синтаксический сахар, в виде свободных переходов, недетерминированности и множеств состояний. Реализовать можно как массив состоящий из структур в которой хранится состояние, входной символ и следующее состояние.
Свободные переходы (эпсилон переходы) — переходы, которые можно совершать без чтения входного символа.
Недетерминированность — ноль и более переходов для одного символа в каких-либо состояниях.
Множества состояний — в один момент времени НКА может находится в нескольких состояниях.
Заключительное состояние обозначается двойным кругом.
В стартовом состоянии у нас текущим состоянием является <1>, при входном символе ‘b’ у нас появляется возможность, пойти в состояние 1 и в состояние 2, то есть после входного символа ‘b’ текущим состоянием является множество <1, 2>.
Свободным переходом обозначается пунктирной линией.
Здесь видно два свободных перехода из стартового состояния, то есть без чтения входного символа мы сразу находимся в множестве состоянии <2, 4>.
Для преобразования НКА в ДКА используется алгоритм Томпсона.
При преобразовании НКА в ДКА может получиться не совсем минимальный ДКА и для его минимизации можно применить алгоритм Бржозовского.
Конечные автоматы с магазинной памятью (pushdown automaton)
Это тот же КА, но с дополнительной памятью в виде стека. Теперь для совершения перехода нужно учитывать еще несколько факторов, символ который нужно удалить из стека и символы которые нужно добавить в стек.
КАМП можно применять в таких местах, где может быть неограниченное количество вложений, например при разборе языков программирование или подсчету вложенных скобок в математических выражениях. Реализовать с помощью КА невозможно, ведь количество возможных состояний конечно в отличие от стека (я понимаю, что память тоже конечна).
Удаление символа из стека — при любом переходе решается какой символ вытолкнуть, если на вершине стека не оказалось такого символа, то он и не выталкивается. Так же если символ нужно оставить в стеке, то он добавляется вместе с добавляемыми символами.
Добавление символов в стек — при любом переходе решает какие символы добавить в стек.
Этот КАМП подсчитывает вложенность скобок, за счет добавления и удаления символов из стека.
ДАМП не равен НАМП, поэтому невозможно одно преобразовать в другое, следовательно НАМП обладает преимуществом перед ДАМП.
Машина Тьюринга (Turing machine)
Самая мощная машина из существующих, его преимущество перед другими в ленте с которой он может работать как хочет. В нем нет свободных переходов. Умеет интерпретировать другие автоматы такие как КА, КАМП.
Лента — это одномерный массив в который могут записываться данные за счет головки над ячейкой, который можно заранее заполнить входными данными.
Шаблон: считаный_символ_с_головки/записаный_символ; сторона_смещения_головки. края ленты обозначаются ‘_’.
Эта МТ выполняет инкремент двоичного числа, головка стоит слева, там где начинается лента.
ДМТ эквивалентен НМТ, так, что они тоже не различаются.
Универсальная машина Тьюринга (universal Turing machine)
Машина которая может порождать другие машины Тьюринга, получая на входную ленту данные машины.
Конечный автомат: теория и реализация
Конечный автомат — это некоторая абстрактная модель, содержащая конечное число состояний чего-либо. Используется для представления и управления потоком выполнения каких-либо команд. Конечный автомат идеально подходит для реализации искусственного интеллекта в играх, получая аккуратное решение без написания громоздкого и сложного кода. В данной статье мы рассмотрим теорию, а также узнаем, как использовать простой и основанный на стеке конечный автомат.
Мы уже публиковали серию статей по написанию искусственного интеллекта при помощи конечного автомата. Если вы еще не читали эту серию, то можете сделать это сейчас:
Примечание автора Хоть в статье используются ActionScript 3 и Flash, вы с легкостью можете писать на удобном для вас языке.
Что такое конечный автомат?
Конечный автомат (или попросту FSM — Finite-state machine) это модель вычислений, основанная на гипотетической машине состояний. В один момент времени только одно состояние может быть активным. Следовательно, для выполнения каких-либо действий машина должна менять свое состояние.
Конечные автоматы обычно используются для организации и представления потока выполнения чего-либо. Это особенно полезно при реализации ИИ в играх. Например, для написания «мозга» врага: каждое состояние представляет собой какое-то действие (напасть, уклониться и т. д.).
Описание состояний автомата
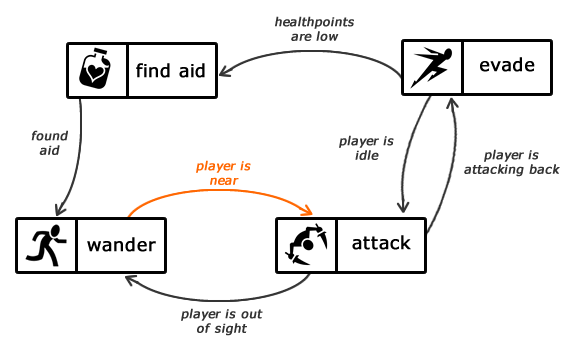
Конечный автомат можно представить в виде графа, вершины которого являются состояниями, а ребра — переходы между ними. Каждое ребро имеет метку, информирующую о том, когда должен произойти переход. Например, на изображении выше видно, что автомат сменит состояние «wander» на состояние «attack» при условии, что игрок находится рядом.
Планирование состояний и их переходов
Реализация конечного автомата начинается с выявления его состояний и переходов между ними. Представьте себе конечный автомат, описывающий действия муравья, несущего листья в муравейник:
Описание состояний интеллекта муравья
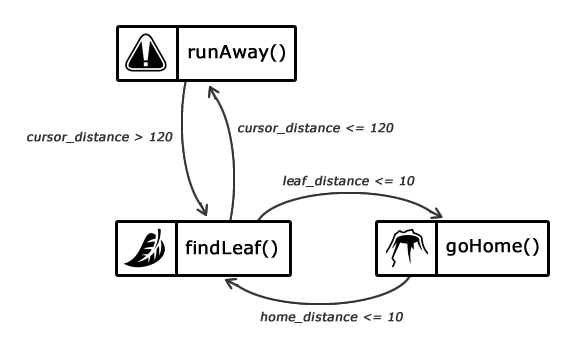
Отправной точкой является состояние «find leaf», которое остается активным до тех пор, пока муравей не найдет лист. Когда это произойдет, то состояние сменится на «go home». Это же состояние останется активным, пока наш муравей не доберется до муравейника. После этого состояние вновь меняется на «find leaf».
27–29 декабря, Онлайн, Беcплатно
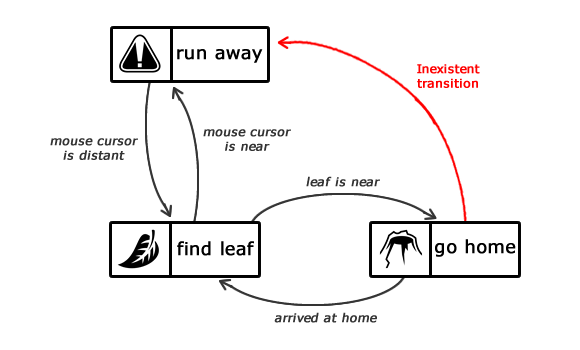
Если состояние «find leaf» активно, но курсор мыши находится рядом с муравьем, то состояние меняется на «run away». Как только муравей будет в достаточно безопасном расстоянии от курсора мыши, состояние вновь сменится на «find leaf».
Обратите внимание на то, что при направлении домой или из дома муравей не будет бояться курсора мыши. Почему? А потому что нет соответствующего перехода.
Описание состояний интеллекта муравья. Обратите внимание на отсутствие перехода между «run away» и «go home»
Реализация простого конечного автомата
Конечный автомат можно реализовать при помощи одного класса. Назовем его FSM. Идея состоит в том, чтобы реализовать каждое состояние как метод или функцию. Также будем использовать свойство activeState для определения активного состояния.
Всякое состояние есть функция. Причем такая, что она будет вызываться при каждом обновлении кадра игры. Как уже говорилось, в activeState будет храниться указатель на функцию активного состояния.
Метод update() класса FSM должен вызываться каждый кадр игры. А он, в свою очередь, будет вызывать функцию того состояния, которое в данный момент является активным.
Метод setState() будет задавать новое активное состояние. Более того, каждая функция, определяющая какое-то состояние автомата, не обязательно должна принадлежать классу FSM — это делает наш класс более универсальным.
Использование конечного автомата
Давайте реализуем ИИ муравья. Выше мы уже показывали набор его состояний и переходов между ними. Проиллюстрируем их еще раз, но в этот раз сосредоточимся на коде.
Описание состояний интеллекта муравья, сосредоточенное на коде
Наш муравей представлен классом Ant, в котором есть поле brain. Это как раз экземпляр класса FSM.
Класс Ant также содержит свойства velocity и position. Эти переменные будут использоваться для расчета движения с помощью метода Эйлера. Функция update() вызывается при каждом обновлении кадра игры.
Для понимания кода мы опустим реализацию метода moveBasedOnVelocity(). Если хотите узнать поподробнее на тему движения, прочитайте серию статей Understanding Steering Behaviors.
Ниже приводится реализация каждого из методов, начиная с findLeaf() — состояния, ответственного за поиск листьев.
Состояние goHome() — используется для того, чтобы муравей отправился домой.
И, наконец, состояние runAway() — используется при уворачивании от курсора мыши.
Улучшение FSM: автомат, основанный на стеке
Представьте себе, что муравью на пути домой также нужно убегать от курсора мыши. Вот так будут выглядеть состояния FSM:
Обновленное описание состояний интеллекта муравья
Кажется, что изменение тривиальное. Нет, такое изменение создает нам проблему. Представьте, что текущее состояние это «run away». Если курсор мыши отдаляется от муравья, что он должен делать: идти домой или искать лист?
Решением такой проблемы является конечный автомат, основанный на стеке. В отличие от простого FSM, который мы реализовали выше, данный вид FSM использует стек для управления состояниями. В верхней части стека находится активное состояние, а переходы возникают при добавлении/удалении состояний из стека.
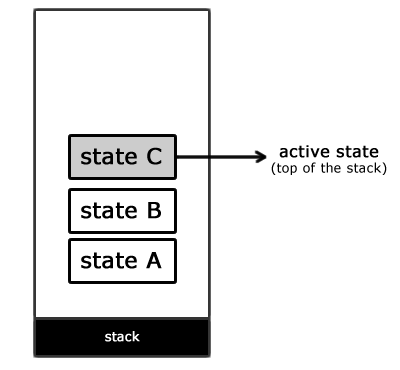
Конечный автомат, основанный на стеке
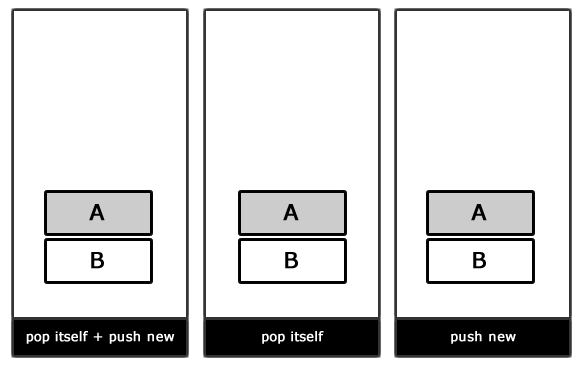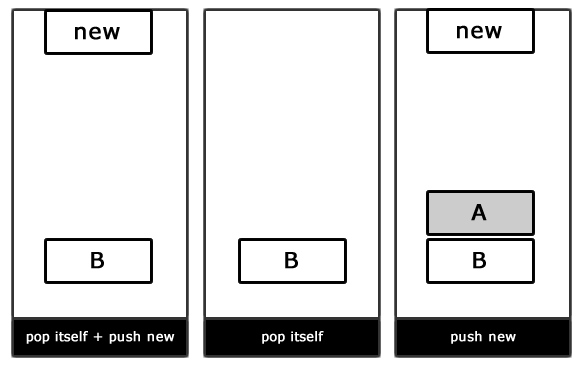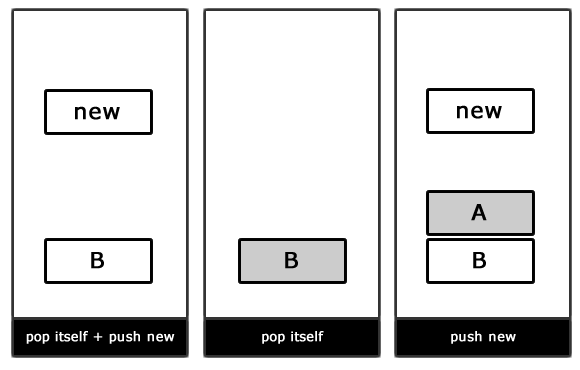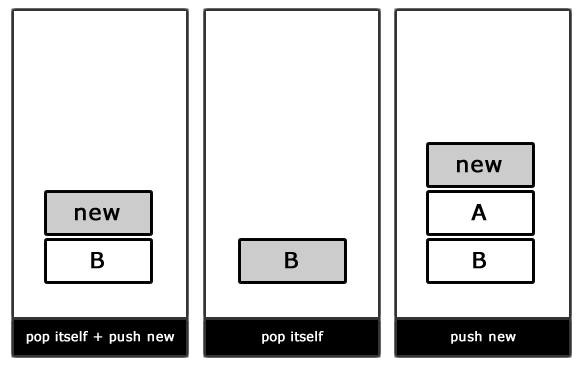
А вот и наглядная демонстрация работы конечного автомата, основанного на стеке:
Переходы в FSM, основанном на стеке
Реализация FSM, основанного на стеке
Такой конечный автомат может быть реализован так же, как и простой. Отличием будет использование массива указателей на необходимые состояния. Свойство activeState нам уже не понадобится, т.к. вершина стека уже будет указывать на активное состояние.
Обратите внимание, что метод setState() был заменен на pushState() (добавление нового состояния в вершину стека) и popState() (удаление состояния на вершине стека).
Использование FSM, основанного на стеке
Важно отметить, что при использовании конечного автомата на основе стека каждое состояние несет ответственность за свое удаление из стека при отсутствии необходимости в нем. Например, состояние attack() само должно удалять себя из стека в том случае, если враг был уже уничтожен.
Вывод
Конечные автоматы, безусловно, полезны для реализации логики искусственного интеллекта в играх. Они могут быть легко представлены в виде графа, что позволяет разработчику увидеть все возможные варианты.
Реализация конечного автомата с функциями-состояниями является простым, но в то же время мощным методом. Даже более сложные переплетения состояний могут быть реализованы при помощи FSM.