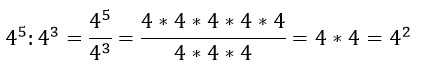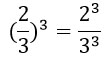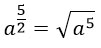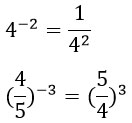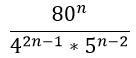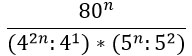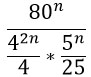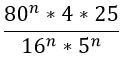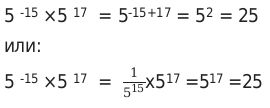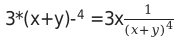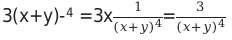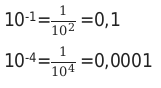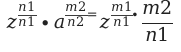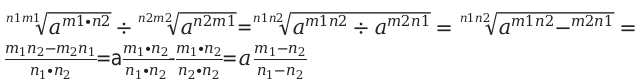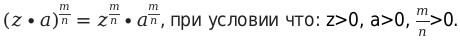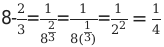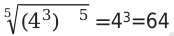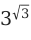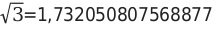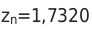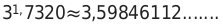степень что такое в алгебре
Степени и их свойства
Данная тема очень легкая, если выучить все свойства степеней. Они, кстати, достаточно просты для запоминания.
Перед тем, как перейти в свойствам степеней, разберемся, что такое степень.
Показатель степени показывает (масло масляное) сколько раз мы умножаем основание на себя. Это очень хорошо проглядывается на следующих примерах:
Вроде бы ничего сложного нет, правда?
Что ж, время перейти к свойствам.
Свойства степеней.
1. Любое число в первой степени равно самому себе: a 1 = a.
Сразу рассмотрим примеры.
2. Любое число в нулевой степени равно 1: а 0 = 1.
3. Единица в любой степени равна 1: 1 n = 1.
Это свойство легко доказать на числовом примере.
Конечно, так никто не расписывает, а сразу пользуется готовой формулой. Вот еще несколько примеров:
3 4 · 3 9 · 3 15 = 3 4 + 9 + 15 = 3 2 8 ;
Еще парочка примеров:
(2 2 ) 3 = 2 2 · 3 = 2 6 ;
8. Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень: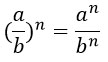
9. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле 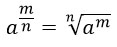
10. Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса: 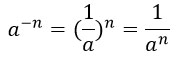
Это же правило работает и для дробей: 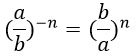
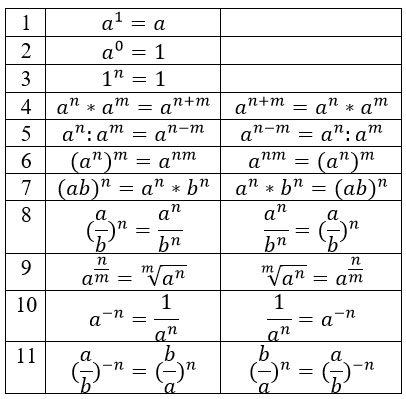
Все эти свойства срабатывают как в одну сторону, так и в другую. Соберем их в аккуратную табличку.
Нам нужно сократить такую дробь:
Преобразуем знаменатель дроби, дважды использовав формулу по номером 5 из второго столбика таблицы.
Получившиеся частные в знаменателе запишем в виде дробей.
Получилась трехярусная дробь (можно произведение дробей в знаменателе переписать под одну черту). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх 🙂
Переходим к финалу. Преобразуем знаменатель по свойству 7 из второго столбика таблицы (снова) и, наконец-таки, сокращаем дробь!
Что такое степень числа
Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.
Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.
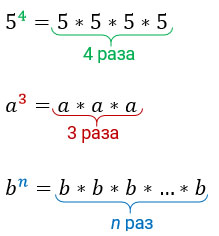
Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.
Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».
4 · 4 · 4 · 4 · 4 · 4 = 4 6
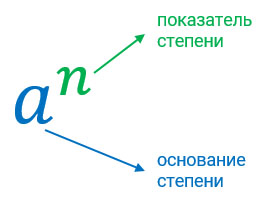
Выражение 4 6 называют степенью числа, где:
В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:
Исключение составляют записи:
Конечно, выражения выше можно читать и по определению степени:
Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a
Любое число в нулевой степени равно единице.
a 0 = 1
Ноль в любой натуральной степени равен нулю.
0 n = 0
Единица в любой степени равна 1.
1 n = 1
Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.
При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.
Пример. Возвести в степень.
Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.
При возведении в степень положительного числа получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.
Квадрат любого числа есть положительное число или нуль, то есть:
Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.
Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.
В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:
Пример. Вычислить: −6 2 − (−1) 4
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.
Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.
Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».
Определение степени с натуральным показателем
Степень с натуральным показателем — что такое в алгебре
Степень в алгебре состоит из двух компонентов: основания и показателя. Основание степени — любое число. Показатель — число, которое показывает, сколько раз нужно умножить основание само на себя.
В математике — это степень, показатель которой является натуральным числом.
Вспомним, что натуральными называют все целые числа больше нуля. Так, числа 1; 365; 1890 будут натуральными, а числа 0; –9; 8,7 — нет.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Основные определения, свойства
Степенью числа a с натуральным показателем n называется произведение n одинаковых множителей, каждый из которых равен a.
Иногда возникают особые случаи решения данного выражения, а именно:
За исключением этих случаев, чтобы производить вычисления и различные действия со степенями, нужно знать основные свойства:
4. При возведении в степень произведения каждый множитель возводится в данную степень.
Правила работы со степенями с одинаковым показателем
Рассмотрим задания на решение выражений с одинаковыми показателями.
У них тоже есть определенные свойства, а именно:
\(a^n\times b^n=\left(a\times b\right)^n;\)
Решение вычислительных примеров
Если вы выучите основные свойства степеней и запомните все формулы, то сможете приступить к решению примеров со степенями. Давайте попробуем потренироваться и решить примеры разных уровней сложности.
Задание: возвести число 3 в 4-ю степень.
По определению четвертой степенью числа три является произведение четырех множителей, каждый из которых равен трем.
Задание в примерах 2-10 — вычислить:
По свойству степени при умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются.
По свойству степени при делении степеней с одинаковыми основаниями основание остается прежним, а из показателя первой степени вычитается показатель второй.
По свойству степени при возведении степени в степень основание остается прежним, а показатели перемножаются.
По свойству степени при возведении в степень произведения каждый множитель возводится в данную степень.
По свойству степени при возведении в степень дроби в данную степень возводится и числитель, и знаменатель.
По свойству степени при умножении степеней с одинаковыми показателями показатель остается прежним, а основания степеней перемножаются.
По свойству степени при делении степеней с одинаковыми показателями показатель остается прежнем, а основание первой степени делится на основание второй.
Попробуем решить еще два выражения, более сложных.
Помним о порядке действий. Сперва — умножение в скобках, потом — деление. Воспользуемся знаниями о свойствах степеней и получим следующее
Воспользуемся знаниями о свойствах степеней и получим следующее:
Основные определения и свойства степеней в математике
Время чтения: 30 минут
В предложенном материале мы подробно будем изучать степени, их свойства. И постараемся весь изученный материал усвоить на примерах.
В этой статье мы подробно изучим, что такое степень числа. Разберемся и охарактеризуем определения степени числа. При этом выучим все существующие в математике показатели степени. Начиная от натурального числового показателя, заканчивая рациональным показателем.
Весь материал попутно будем рассматривать, и закреплять на конкретных примерах.
Перед тем, как приступить к изучению основных свойств степеней, разберем следующие основные определения, которые нам понадобятся в процессе всего изучения материала определения:
Степень числового значения — это перемноженные между собой одинаковые значения.
Разберем данное определение на примерах:
Левую часть равенства можно упростить. Для начала указать множитель, который повторяется, и обозначить количество его повторений. Повторяющийся множитель в данном случае это 2. Дублируется он три и шесть раз соответственно. Поэтому над двойкой записываем 3 и 6:
Формулировка выражений звучит следующим образом:
Основание выражения степени — это числовое или буквенное значение, которое повторяется в выражении не однократно.
В вышеизложенных выражениях — это число два.
Показатель степени — это значение, которое отображает, количество повторений основания степени.
В примере, мы видим, что число 5 и 6 повторяется три раза, так как степень, в которую нужно возвести число равняется трем.
Если степень, будет иметь иное значение. Например: 7, то показатель степени будет равняться семи.
Иными словами, приведенный расчет называется приведением в степень.
Например: нам необходимо определить произведение пяти одинаковых чисел, каждый из них равен 3, то правильно будет сказано, что число 3 возводится в пятую степень:
Видим, что число три в пятой степени равняется числу 243.
Для закрепления разберем еще несколько простых примеров.
Пример 1.
Пример 2.
Пример 3
Степени, так же подразделяются на:
В алгебре, да и, в общем, в математике, степень, как правило, имеет четыре основных свойства:
В данном уроке, мы поочередно разберемся с каждым свойством, его особенностями расчетов. Закрепим материал на конкретных примерах с применением числовых данных.
Свойство степени с натуральным показателем и особенности вычисления
Натуральный показатель степени имеет следующие свойства:
а) Главное свойство:
Равенство является верным при любых значениях m и n. И действительном значении а.
Равенство мы разберем на конкретном числовом примере:
Мы имеем две степени с основание четыре.
Натуральные показатели имеют значения три, и пять соответственно.
Составим равенство, подставляя числовые значения:
4 3 x4 5 =(4·4·4)(4·4·4·4·4)=64×1024=65536 или 4 8 =4·4·4·4·4·4·4·4=65536
Решив равенство, мы получаем: 4 3 4 5 =4 8
Тем самым, мы видим, что равенство доказано.
Также, используя свойство умножения, можно обобщить свойства. Если в равенстве представлены от трех и более степеней. Натуральные числа обозначим m1, m2.
Составим несколько равенство, подставляя числовые значения, для лучшего усвоения:
(2) 2 (2) 3 (2) 3 (2) 4 =(2) 2+3+3+4 =(2) 12
(3) 2 (3) 3 (3) 3 (3) 4 =(3) 2+3+3+4 =(3) 12
(5) 2 (5) 3 (5) 3 (5) 4 =(5) 2+3+3+4 =(5) 12
б) Свойство частных степени, когда основания имеют одинаковые значения
Свойство частных имеет следующий вид, в виде равенства:
Оно справедливо при любых натуральных значений n и m, любом значении x, кроме нуля. Значение основания, нельзя принимать равным нулю. В противном случае при расчете, придется делить на ноль, что по правилам математики недопустимо.
Так же, есть еще одно условие: значение n должно быть больше, значения m. После вычета должно получится положительное число.
Для доказательства условия, составим равенство:
x n-m x m =x (n-m)+m =x n
Преобразовав равенство, мы можем вывести следующий пример:
Для наглядности, подставим числовые значения:
в) Произведение степеней
Степень произведения можно выразить в виде равенства:
Равенство можно преобразовать в следующей вид:
(xy) m =(xy)(xy). (xy), количество множителей равно числовому значению степени.
Рассмотрим несколько равенств с числовыми значениями:
— Вариант для положительных значений:
— Вариант для дробей:
— Вариант отрицательных значений:
г) Возведение частного в натуральную степень.
Составим равенство для доказательства данного свойства.
Должны соблюдаться следующие условия:
Для доказательств равенства распишем пример:
Для закрепления знаний, решим несколько примеров, заменяя буквенные значения числовыми.
д) Принцип возведения степени в степень
(2 5 ) 4 =2 5 x 4 =2 20
Также, данное свойство, может быть выражено и несколькими степенями, в виде:
((((x n ) b ) a ) m =x n·x·b·a·m
Для решения равенства, такого типа, необходимо перемножить между собой значение степеней.
((((32) 3 ) 4 ) 2 =3 2342 =3 48
((((5) 3 ) 4 ) 2 =5 2342 =5 48
((((12) 3 ) 4 ) 6 =3 2346 =3 192
е) Принципы равенства и неравенства.
Данный принцип звучит следующим образом: большее значение имеет степень, у которой значение основания степени большее или наоборот.
Например:
x 2 2 или подставив числовые значения, образует вид: 4 5 5
Еще несколько примеров для закрепления, с разными числовыми значениями:
Как видно из примеров, равенство верно, в том случае если значение основания больше.
Принцип неравенства считается верным, если одна степень больше значения другой, а основание больше нуля, но не меньше единицы. То есть, числовое значение должно быть положительным.
Степень с целым показателем и ее свойства
После того как мы определили степень числа с натуральным показателем, мы можем дальше продолжать расширять знания о степени и перейти к степени числа, показателем которой является любое число, в том числе и отрицательное и ноль. Из этого следует, чтобы оставались правильными все свойства степени, потому что натуральные числа являются составляющей целых чисел.
Степень с целым показателем — это степень, когда любое целое число, является показателем.
Натуральный вид степени тоже является степенью с целым показателем, потому что натуральные числовые значения так же являются целыми числами.
Для степеней с целыми положительными показателями, свойства аналогичны, как и для натуральных показателей.
Рассмотрим основные свойства степеней с целыми показателями.
Рассмотрим следующую последовательность степеней:
3 0 3 1 3 2 3 3 3 4 3 5 3 6 3 7
Продолжим решать значения с отрицательными степенями:
Теперь определим степени с натуральным значением и с нулем.
Расчеты приведены в таблице 1
Таблицы 1. Расчет степени с натуральными показателями и с нулем
| Значение степени | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Результат вычисления | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Если вычисление положительных значений и нуля, особых трудностей не вызывает. А что делать с отрицательными показателями? На этот вопрос мы ответим далее.
При возведении в положительную степень, как правило, число имеет большее значение. А вот при вычислении в отрицательной степени, результат будет иметь меньшее значение.
Если для примера взять число z, и начать поочередно увеличивать его степень, то в результате мы увидим поочередность чисел, где последующее число меньше следующего в z раз.
Для примера, возьмем число 4.Начало расчета возьмем ноль и будем поочередно повышать степень. Далее найдем значение при вычислении.
Расчеты приведены в таблицу 2.
Таблицы 2. Расчет степени с натуральными показателями.
| Значение степени | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Результат вычисления | 1 | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 |
Получили перечень чисел, в котором каждое число больше предыдущего числа в четыре раза. Тогда правильно предположить, что число, которое имеет значение больше единицы, будет в четыре раза больше единицы.
Предыдущее за числом 1/4 должно быть в два раза меньше. Чтобы его получить разделим 1/4 на 2.
Отсюда следует, что 1/4>1/16 в четыре раза.
Выполняя деление на четыре определим значения других степеней с целыми отрицательными показателями:
Расчеты приведены в таблицу 3.
Таблицы 3. Расчет степени с целыми отрицательными значениями степеней.
| Значение степени | -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| Результат вычисления | 1 | 4 | 16 | 64 | 256 | 1024 | 16384 |
Проанализировав значения в таблице 3, можно сделать следующий вывод: результаты степени с отрицательными значениями, прямо пропорциональны значениям с положительным результатом.
Данные вычисления и сравнения сведем в таблицу 4.
Таблица 4. Сравнение и анализ итоговых данных.
| -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| 1 | 4 | 16 | 64 | 256 | 1024 | 16384 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 |
Решим еще несколько примеров для закрепления материала.
Воспользуемся, уже изученным правилом вычисления значения степеней, у которых значение отрицательное.
Потому что, если z будет равен нулю, в знаменателе число выйдет равным ноль. По правилам математики на ноль делить нельзя.
1.Принцип вычисления тождественных преобразований
Все данные преобразования для натуральных и целых показателей одинаковы. Они, также, сохраняются и для степеней, которые имеют отрицательные значения.
Далее, при помощи примеров, закрепим полученные знания
Пример 1. Найти значение выражения 5 −15 × 5 17
Вариант вычисления, первым способом, легче. Именно его чаще всего и применяют в процессе обучения.
Пример 2. Найти значение выражения (10−4)−1
Используем для расчета правило возведения в степень
(10 −4 ) −1 = 10 −4 × (−1) = 10 4 = 10000
Пример 3. Определить значение выражения (10 −5 ) −1
Для этого применим правилом возведения степени в степень:
(10 −5 ) −1 = 10 −5 × (−1) = 10 5 = 10000
2.Перемещение степени между знаменателем и числителем
В случае если в знаменателе дроби, имеется степень, то ее можно переместить в числитель и при этом необходимо поменять знак на противоположный.
При этом само значение выражения не поменяется.
Данный метод иногда используется при упрощении выражений.
Рассмотрим основные примеры:
Пример 1.
Пример 2. Перемещение значения степени из знаменателя дробного выражения 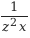
Пример 3. Записать произведение 3x*(x + y) −4 в виде дроби, которая не имеет степени с отрицательным значением.
Затем перемножим множитель 3 с числителем дроби 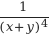
Итоговый результат:
3.Возведение числа 10 в целую отрицательную степень
Вычисление степени для числа 10 происходит таким же образом, как и остальные числа.
На примерах рассмотрим более подробно.
Пример 1:
Если обратить внимание на пример, то мы увидим, что количество нулей в ответе равно показателю самой степени.
Проще говоря, чтобы возвести 10 в отрицательную степень, можно только записать количество необходимых нулей перед единицей. Но, не забыть поставить запятую, перед вторым нулем.
Пример 1:
Пример 2:
Пример 3:
Пример 4:
Пример 5:
4.Преобразование значений 0,1, 0,01, 0,001, где основанием степени является число 10
Если степень представлена числами 0,1; 0,01; 0,001 и основание имеет значение 10. Для преобразования необходимо:
Число 0,01 это значение деления 1/100, или 1/10 2
Пример 2: Значение 0,00001 в виде степени с основанием 10.
5. Вид числа (значения) стандартный
Запишем число 4 000 в следующем виде 4 и 1 000
Именно такое выражение и называют стандартным видом. Он позволяет записывать большие и маленькие числа в более компактном виде.
Пример 1.
Пример 2.
0,158× 10 000 = 0,158× 10 4
Пример 3.
26× 1 000 000 = 26× 10 6
Стандартный вид числа имеет следующее выражение: z × 10m, где 1 ≤ z Нужна помощь
Свойство степени с рациональным показателем
От целых показателей степени числа z мы переходим к рациональным показателем степеням. Далее мы определим степень с рациональным показателем, причем будем производить расчеты так, чтобы сохранялись все свойства степени с целым показателем. Это обязательно, потому что целые числа являются непосредственно частью рациональных чисел.
Свойство степени с рациональным показателем значительно облегчает изучение степеней в целом. Изучив данный метод, можно легко научится решать задачи различного уровня сложности.
Рассмотрим основные свойства степени с рациональным показателем.
а) Произведение степеней с основаниями, которые имеют одинаковые значения.
б) Свойство частного значения.
Доказательство данного свойства идентично по сравнению с предыдущим.
в) Свойство произведения в степень в виде дроби
г) Свойство степени в степени.
д) Свойство сравнения степеней со значениями равными между собой
Отсюда следует неравенство: m m >y m
е) Условие рациональных чисел
x > y при 0 0 z x >z y
Для того чтобы доказать все перечисленные условия, нам необходимо будет вспомнить, понятие степени с дробным показателем.
Рассмотрим свойство с рациональным показателем на примере:
Пример №1.
Пример № 2: необходимо вычислить
Преобразуя уравнение, мы получим следующий вид: 4 15 =(4 3 ) 5 далее записываем в виде
Степень с иррациональным и действительным показателем
Понятно, что множество действительных чисел можно рассматривать как объединение множеств рациональных и иррациональных числовых значений. Поэтому степень с действительным показателем принято считать определенным значением, когда определяются степень с рациональным показателем и степень с иррациональным показателем. Про степень с рациональным показателем было подробно рассмотрено в предыдущем пункте, осталось лишь разобраться подробнее со степенью с иррациональным показателем.
Основные свойства иррациональных чисел:
— сумма из двух положительных иррациональных чисел может равняться рациональным числом.
— множество иррациональных чисел встречаются повсюду на протяжении всей числовой прямой
— между двумя любыми различными рациональными числами имеется иррациональное число.
Свойства иррациональных степеней, как было уже сказано ранее, включают в себя все предыдущие характеристики с других свойств степеней
1. a p ⋅ a q = a p + q ;
2. a p : a q = a p – q ;
3; ( a ⋅ b ) p = a p ⋅ b p ;
4.( a : b ) p = a p : b p ;
6. a p q a p =0 a>0, то a p > a q a p >a q ;
Таким образом, все степени, показатели которых p p и q q являются действительными числами, при условии
a > 0 a>0 обладают теми же свойствами.
Для определения степени с иррациональным показателем, часто конечный результат определяют с точностью до определенного знака.
Для того, чтобы вычислить число в иррациональной степени, нужно его число возвести в дробную степень.
Более точный результат мы получим, при наиболее приближенном значении.
Рассмотрим на примере:
— Вычислим значение корня из 3.
— Определим приближенное значение до четырех цифр после запятой.
— Возведем значение три в степень и получим значение, в виде бесконечной дроби:
— Далее необходимо округлить полученное числовое значение до четырех знаков.
Иррациональный процесс расчета, метод очень трудоемкий. В основном все вычисления в алгебре строятся таким методом, чтобы избавиться от иррациональности. Он несет в себе неудобства расчета, ведь иррациональность не дает возможность получить точность определения окончательного значения.