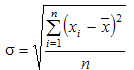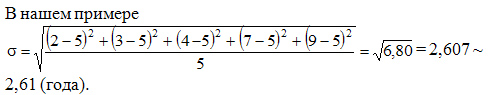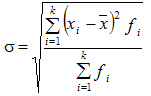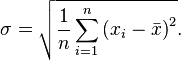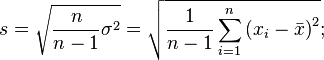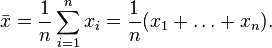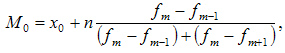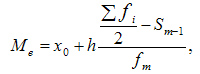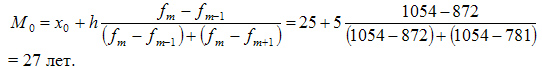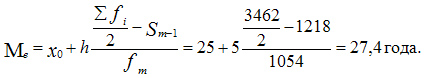стандартное отклонение в чем измеряется
Среднеквадратическое отклонение
Среднеквадрати́ческое отклоне́ние (синонимы: среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.
Содержание
Основные сведения
Измеряется в единицах измерения самой случайной величины. Равно корню квадратному из дисперсии случайной величины. Среднеквадратическое отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины Пол, стены вокруг нас и потолок, x относительно её математического ожидания на основе несмещённой оценки её дисперсии):
Правило трёх сигм
Правило трёх сигм (
) — практически все значения нормально распределённой случайной величины лежат в интервале 
. Более строго — не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина 
истинная, а не полученная в результате обработки выборки).
Интерпретация величины среднеквадратического отклонения
Большое значение среднеквадратического отклонения показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: <0, 0, 14, 14>, <0, 6, 8, 14>и <6, 6, 8, 8>. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределенности. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
Практическое применение
На практике среднеквадратическое отклонение позволяет определить, насколько значения в множестве могут отличаться от среднего значения.
Климат
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Спорт
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
Технический анализ
В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера.
См. также
Литература
 |
 Статистические показатели | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Описательная статистика |
| ||||||||||||
| Статистический вывод и проверка гипотез |
| ||||||||||||
| Корреляция | Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания | ||||||||||||
| Линейные модели | Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ | ||||||||||||
| Регрессия | Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия | ||||||||||||
Полезное
Смотреть что такое «Среднеквадратическое отклонение» в других словарях:
Среднеквадратическое отклонение — мера отклонения опытных данных от выборочного среднего значения или от функциональной зависимости, выражаемая в абсолютных единицах, вычисляется по формулам (4), (12). Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов… … Словарь-справочник терминов нормативно-технической документации
Среднеквадратическое отклонение — показатель связи результатов деятельности взаимного фонда с общей ситуацией на рынке или динамикой соответствующего базового индекса. Если среднеквадратическое отклонение равно 1, то стоимость портфеля фонда в точности повторяет изменения… … Финансовый словарь
Среднеквадратическое отклонение — повторяемости: среднеквадратическое отклонение результатов измерений, полученных в условиях повторяемости (является мерой рассеяния результатов измерений в условиях повторяемости). Источник: ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА… … Официальная терминология
Среднеквадратическое отклонение — * сярэднеквадратычнае адхіленне * mean square deviation or standard deviation описательная статистика (параметр), являющаяся мерой рассеяния для приближенно нормально распределенных данных. Если распределение не соответствует закону нормального… … Генетика. Энциклопедический словарь
среднеквадратическое отклонение — vidutinis kvadratinis nuokrypis statusas T sritis automatika atitikmenys: angl. root mean square deviation vok. mittlere quadratische Abweichung, f rus. среднеквадратическое отклонение, n pranc. écart moyen quadratique, m … Automatikos terminų žodynas
Среднеквадратическое отклонение воспроизводимости — Среднеквадратическое отклонение воспроизводимости: среднеквадратическое отклонение результатов измерений, полученных в условиях воспроизводимости (является мерой рассеяния результатов измерений в условиях воспроизводимости). Источник:… … Официальная терминология
среднеквадратическое отклонение воспроизводимости — 3.6.5.1 среднеквадратическое отклонение воспроизводимости: Среднеквадратическое отклонение результатов измерений, полученных в условиях воспроизводимости (является мерой рассеяния результатов измерений в условиях воспроизводимости). Источник:… … Словарь-справочник терминов нормативно-технической документации
среднеквадратическое отклонение воспроизводимости результатов испытаний — 3.21 среднеквадратическое отклонение воспроизводимости результатов испытаний sR:Среднеквадратическое отклонение результатов испытаний, полученных в условиях воспроизводимости (см. 3.19) [5]. Источник … Словарь-справочник терминов нормативно-технической документации
среднеквадратическое отклонение повторяемости (сходимости) результатов испытаний — 3.24 среднеквадратическое отклонение повторяемости (сходимости) результатов испытаний sr: Среднеквадратическое отклонение результатов испытаний, полученных в условиях повторяемости (сходимости) (см. 3.22) [5]. Источник … Словарь-справочник терминов нормативно-технической документации
среднеквадратическое отклонение (совокупности), стандартное отклонение (совокупности) — 3.13 среднеквадратическое отклонение (совокупности), стандартное отклонение (совокупности) [(population) standard deviation] σ: Положительный квадратный корень из дисперсии совокупности σ2. Источник: ГОСТ Р ИСО 12491 2011: Материалы и изделия… … Словарь-справочник терминов нормативно-технической документации
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Среднее квадратическое отклонение
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение (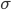 
) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
Среднее квадратическое отклонение простое:
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение:
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Дисперсия, ее виды, среднеквадратическое отклонение.
Дисперсия случайной величины — мера разброса данной случайной величины, т. е. её отклонения отматематического ожидания. В статистике часто употребляется обозначение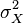 
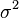
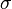
или 
. Квадратный корень из дисперсии 
называется среднеквадратичным отклонением, стандартным отклонением или стандартным разбросом.
Общая дисперсия (σ 2 ) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Вместе с тем, благодаря методу группировок можно выделить и измерить вариацию, обусловленную группировочным признаком, и вариацию, возникающую под влиянием неучтенных факторов.
Межгрупповая дисперсия (σ 2 м.гр) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основание группировки.
Среднеквадратическое отклонение (синонимы: среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение; близкие термины: стандартное отклонение, стандартный разброс) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величиныотносительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическоесовокупности выборок.
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется какквадратный корень из дисперсии случайной величины.
Среднеквадратическое отклонение:
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии):
где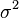 
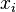
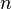
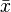
— дисперсия; 
— i-й элемент выборки; 
— объём выборки; 
— среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
Сущность, область применения и порядок определения моды и медианы.
Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
— 
— значение моды
— 
— нижняя граница модального интервала
— 
— величина интервала
— 
— частота модального интервала
— 
— частота интервала, предшествующего модальному
— 
— частота интервала, следующего за модальным
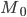
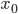
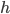
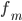
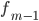
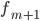
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот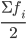 
, а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:
Ме = (n(число признаков в совокупности) + 1)/2,
в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
— 
— искомая медиана
— — нижняя граница интервала, который содержит медиану
— — величина интервала
— 
— сумма частот или число членов ряда
— 
— сумма накопленных частот интервалов, предшествующих медианному
— — частота медианного интервала
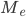
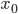
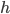
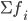
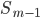
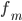
Пример. Найти моду и медиану.
| Возрастные группы | Число студентов | Сумма накопленных частот ΣS |
| До 20 лет | ||
| 20 — 25 | ||
| 25 — 30 | ||
| 30 — 35 | ||
| 35 — 40 | ||
| 40 — 45 | ||
| 45 лет и более | ||
| Итого |
Решение:
В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).
Рассчитаем величину моды:
Это значит что модальный возраст студентов равен 27 годам.
Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σfi/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.
Кроме моды и медианы могут быть использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили — 10 частей и перцентили — на 100 частей.
Понятие выборочного наблюдения и область его применения.
Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.
Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.
Существует 4 способа случайного отбора в выборку:
Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная.
При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.
Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.
Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.
Предельная ошибка выборки наблюдения, средняя ошибка выборки, порядок их расчета.
Рассмотрим подробно перечисленные выше способы формирования выборочной совокупности и возникающие при этом ошибки репрезентативности.
Собственно-случайная выборка основывается на отборе единиц из генеральной совокупности наугад без каких-либо элементов системности. Технически собственно-случайный отбор проводят методом жеребьевки (например, розыгрыши лотерей) или по таблице случайных чисел.
Собственно-случайный отбор «в чистом виде» в практике выборочного наблюдения применяется редко, но он является исходным среди других видов отбора, в нем реализуются основные принципы выборочного наблюдения. Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки.
Ошибка выборочного наблюдения – это разность между величиной параметра в генеральной совокупности, и его величиной, вычисленной по результатам выборочного наблюдения. Для средней количественного признака ошибка выборки определяется
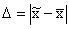
Показатель 
называется предельной ошибкой выборки.
Выборочная средняя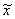 
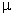
является случайной величиной, которая может принимать различные значения в зависимости от того, какие единицы попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки 
, которая зависит от:
— объема выборки: чем больше численность, тем меньше величина средней ошибки;
— степени изменения изучаемого признака: чем меньше вариация признака, а, следовательно, и дисперсия, тем меньше средняя ошибка выборки.