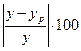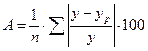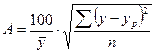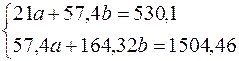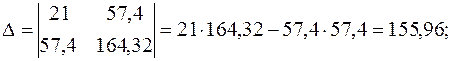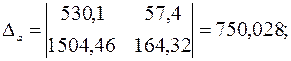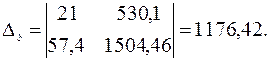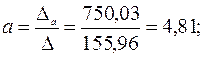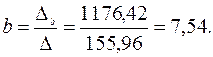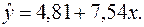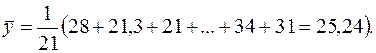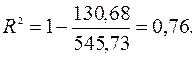средняя ошибка аппроксимации показывает что

Средняя ошибка аппроксимации

По семи территориям Уральского района за 199Х г. известны значения двух признаков.

Район	Расходы на покупку продовольственных товаров в общих расходах, %, у	Среднедневная заработная плата одного работающего, руб., х
Удмуртская респ.	68,8	45,1
Свердловская обл.	61,2	59,0
Башкортостан	59,9	57,2
Челябинская обл.	56,7	61,8
Пермская обл.	55,0	58,8
Курганская обл.	54,3	47,2
Оренбургская обл.	49,3	55,2

Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации А_ср и F-критерий Фишера.

Для наших данных система уравнений имеет вид

F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.

Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Источник

Средняя ошибка аппроксимации

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака каждому наблюдению представляет собой ошибку аппроксимации. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (y – ) несравнимы между собой, исключая величину, равную нулю. Так, если для одного наблюдения y – = 5, а для другого – 10, то это не означает, что во втором случае модель дает вдвое худший результат. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям. Например, если для первого наблюдения y = 20, а для второго y = 50, ошибка аппроксимации составит 25 % для первого наблюдения и 20 % – для второго.

Поскольку (y – ) может быть величиной как положительной, так и отрицательной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Отклонения (y – ) можно рассматривать как абсолютную ошибку аппроксимации, а

– как относительную ошибку аппроксимации. Для того, чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации как среднюю арифметическую простую

. (2.38)

По нашим данным представим расчет средней ошибки аппроксимации для уравнения Y = 6,136 × Х 0,474 в следующей таблице.

Таблица. Расчет средней ошибки аппроксимации

y	yx	y –
6	6,135947	-0,135946847	0,022658
9	8,524199	0,475801308	0,052867
10	10,33165	-0,331653106	0,033165
12	11,84201	0,157986835	0,013166
13	13,164	-0,163999272	0,012615
Итого	0,134471

A = (0,1345 / 5) × 100 = 2,69 %, что говорит о хорошем качестве уравнения регрессии, ибо ошибка аппроксимации в пределах 5-7 % свидетельствует о хорошем подборе модели к исходным данным.

Возможно и другое определение средней ошибки аппроксимации:

(2.39)

Для нашего примера эта величина составит:

.

Для расчета средней ошибки аппроксимации в стандартных программах чаще используется формула (2.39).

Аналогично определяется средняя ошибка аппроксимации и для уравнения параболы.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

1) быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то нужно придать ему количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы);

2) не должны быть коррелированны между собой и тем более находиться в точной функциональной связи.

Включение в модель факторов с высокой интеркорреляцией, когда r_yx1

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы всегда будут действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.

Если рассматривается регрессия y = a + b × x + c × z + d × v + e, то для расчета параметров с применением МНК предполагается равенство

где S 2 _y – общая сумма квадратов отклонений ; S 2 _факт – факторная (объясненная) сумма квадратов отклонений ; S 2 _e – остаточная сумма квадратов отклонений .

В свою очередь, при независимости факторов друг от друга выполнимо равенство

где S 2 _x, S 2 _z, S 2 _v – суммы квадратов отклонений, обусловленные влиянием соответствующих факторов.

Если же факторы интеркоррелированы, то данное равенство нарушается.

Включение в модель мультиколлинеарных факторов нежелательно по следующим причинам:

– затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;

– оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величина, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Для оценки факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрицы парных коэффициентов корреляции между ними была бы единичной, поскольку все недиагональные элементы r_xixj (x_i ¹ x_j) были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных,

матрица коэффициентов корреляции между факторами имела бы определитель, равный единице

,

Если же между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю

.

Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных H₀: DetïRï = 1. Доказано, что величина имеет приближенное распределение c 2 с df = m × (m – 1)/2 степенями свободы. Если фактическое значение c 2 превосходит табличное (критическое): c 2 _факт > c 2 _{табл(df,a)} то гипотеза H₀ отклоняется. Это означает, что DetïRï ¹ 1, недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.

Через коэффициенты множественной детерминации можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение коэффициента множественной детерминации к единице, тем сильна проявляется мультиколлинеарность факторов. Сравнивая между собой коэффициенты множественной детерминации факторов R 2 _{x1ïx2x3…xp}; R 2 _{x2ïx1x3…xp} и т.п., можно выделить переменные, ответственные за мультиколлинеарность, следовательно, можно решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной коэффициента множественной детерминации.

Имеется ряд подходов преодоления сильной межфакторной корреляции. Самый простой из них состоит в исключении из модели одного или нескольких факторов. Другой путь связан с преобразованием факторов, при котором уменьшается корреляция между ними. Например, при построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней Dy = y_t – y_t–1, чтобы исключить влияние тенденции, или используются такие методы, которые сводят к нулю межфакторную корреляцию, т.е. переходят от исходных переменных к их линейным комбинациям, не коррелированным друг с другом (метод главных компонент).

Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если y = f(x₁, x₂, x₃). то можно построить следующее совмещенное уравнение:

Рассматриваемое уравнение включает эффект взаимодействия первого порядка. Можно включать в модель и взаимодействие более высоких порядков, если будет доказана его статистическая значимость, например включение взаимодействия второго порядка b₁₂₃ × x₁× x₂ × x₃ и т.д. Как правила, взаимодействие третьего и более высоких порядков оказывается статистически незначимым; совмещенные уравнения регрессии ограничиваются взаимодействием первого и второго порядков. Но и оно может оказаться несущественным. Тогда нецелесообразно включать в модель взаимодействие всех факторов и всех порядков. Так, если анализ совмещенного уравнения показал значимость только взаимодействия факторов x₁×и x₃, то уравнение будет иметь вид:

Взаимодействие факторов x₁×и x₃ означает, что на разных уровнях фактора x₃ влияние фактора x₁×на y будет неодинаково, т.е. оно зависит от значений фактора x₃. На рис. 3.1 взаимодействие факторов представляется непараллельными линиями связи x₁×с результатом y. И, наоборот, параллельные линии влияния фактора x₁×на y при разных уровнях фактора x₃ означают отсутствие взаимодействия факторов x₁×и x₃.

Рис. 3.1. Графическая иллюстрация взаимодействия факторов

Совмещенные уравнения регрессии строятся, например, при исследовании эффекта влияния на урожайность разных видов удобрений (комбинаций азота и фосфора).

Решению проблемы устранения мультиколлинеарности факторов может помочь и переход к уравнениям приведенной формы. С этой целью в уравнение регрессии подставляют рассматриваемый фактор, выраженный из другого уравнения.

Пусть, например, рассматривается двухфакторная регрессия вида y_x = a + b₁ × x₁ + b₂ × x₂, для которой факторы x₁×и x₂ обнаруживают высокую корреляцию. Если исключить один из факторов, то мы придем к уравнению парной регрессии. Вместе с тем можно оставить факторы в модели, но исследовать данное двухфакторное уравнение регрессии совместно с другим уравнением, в котором фактор (например, x₂) рассматривается как зависимая переменная. Предположим, что x₂ = A + B ×y + C × x₃. Подставив это уравнение в искомое вместо x₂, получим:

Если (1 – b₂ × B) ¹ 0, то, разделив обе части равенства на (1 – b₂ × B), получим уравнение вида

,

которое принято называть приведенной формой уравнения для определения результативного признака y. Это уравнение может быть представлено в виде

К нему для оценки параметров может быть применен метод наименьших квадратов.

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм её решения на компьютере.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

– шаговый регрессионный анализ.

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты – отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).

На первый взгляд может показаться, что матрица парных коэффициентов корреляции играет главную роль в отборе факторов. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут в полной мере решать вопрос о целесообразности включения в модель того или иного фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результатом. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. Отсев факторов можно проводить и по t-критерию Стьюдента для коэффициентов регрессии: из уравнения исключаются факторы с величиной t-критерия меньше табличного. Так, например, уравнение регрессии составило:

В скобках приведены фактические значения t-критерия для соответствующих коэффициентов регрессии, как правило, при t

Источник

Средняя ошибка аппроксимации

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака каждому наблюдению представляет собой ошибку аппроксимации. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.

Поскольку 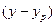может быть величиной как положительной, так и отрицательной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Такие ошибки являются относительными, а отклонения 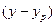можно рассматривать как абсолютные ошибки аппроксимации.

Для того, чтобы иметь общее суждение о качестве модели из относительных отклонений, находят среднюю ошибку аппроксимации как

Ошибка аппроксимации в пределах 5-7 % свидетельствует о хорошем подборе модели к исходным данным.

Возможно и другое определение средней ошибки аппроксимации:

Для расчета средней ошибки аппроксимации в стандартных программах чаще используется вторая формула.

Источник

Средняя ошибка аппроксимации.

Другой показатель качества построенной модели –– среднее относительное отклонение расчетных значений от фактических или средняя ошибка аппроксимации:

.

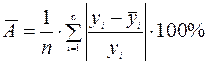
Пример.

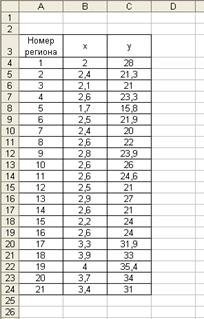
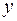
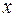
По 21 региону страны изучается зависимость розничной продажи телевизоров ( ) от среднедушевого денежного дохода в месяц ( ).

Номер региона	Среднедушевой денежный доход в месяц, тыс. руб.,	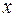Объем розничной продажи телевизоров, тыс. шт.,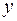
2,4	21,3
2,1
2,6	23,3
1,7	15,8
2,5	21,9
2,4
2,6
2,8	23,9
2,6
2,6	24,6
2,5
2,9
2,6
2,2
2,6
3,3	31,9
3,9
35,4
3,7
3,4

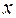
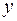
Необходимо найти зависимость, наилучшим образом отражающую связь между переменными и .

Рассмотрим вопрос применения модели линейной регрессии в этой задаче.

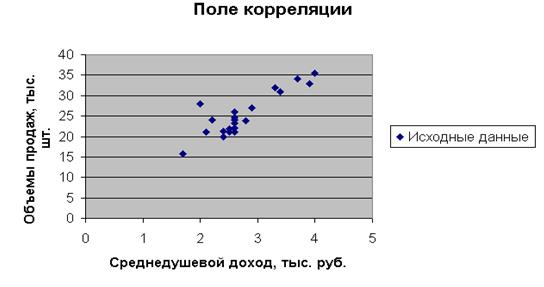
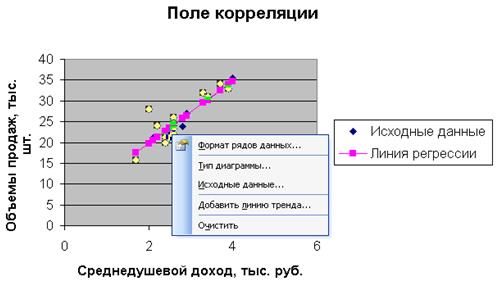
Построим поле корреляции, т.е. нанесем исходные данные на координатную плоскость. Для этого воспользуемся, например, возможностями MS Excel 2003.

Подготовим таблицу исходных данных.

Нанесем на координатную плоскость исходные данные:

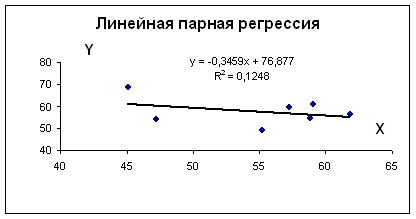
Характер расположения точек на графике дает нам основание предположить, что искомая функция регрессии линейная: 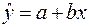. Для оценки коэффициентов уравнения регрессии необходимо составить и решить систему нормальных уравнений ( ).

По исходным данным рассчитываем необходимые суммы:

Номер региона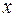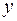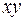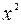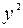
2,4	21,3	51,12	5,76	453,69
2,1	44,1	4,41
2,6	23,3	60,58	6,76	542,89
1,7	15,8	26,86	2,89	249,64
2,5	21,9	54,75	6,25	479,61
2,4	5,76
2,6	57,2	6,76
2,8	23,9	66,92	7,84	571,21
2,6	67,6	6,76
2,6	24,6	63,96	6,76	605,16
2,5	52,5	6,25
2,9	78,3	8,41
2,6	54,6	6,76
2,2	52,8	4,84
2,6	62,4	6,76
3,3	31,9	105,27	10,89	1017,61
3,9	128,7	15,21
35,4	141,6	1253,16
3,7	125,8	13,69
3,4	105,4	11,56
Сумма	57,4	530,1	1504,46	164,32	13926,97

Составляем систему уравнений:

Имеем систему линейных алгебраических уравнений, которая может быть решена, например, по формулам Крамера. Для этого вычислим следующие определители:

Тогда, согласно теореме Крамера,

Получаем уравнение регрессии:

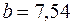
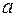
Величина коэффициента регрессии означает, что увеличение среднедушевого месячного дохода на 1 тыс. руб. приведет к увеличение объема розничной продажи в среднем на 7 540 телевизоров. Коэффициент в данном случае не имеет содержательной интерпретации.

Оценим тесноту линейной связи между переменными и качество построенной модели в целом.

Для оценки тесноты линейной зависимости рассчитаем коэффициент детерминации. Для этого необходимо провести ряд дополнительных вычислений.

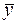
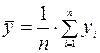
Прежде всего, найдем выборочное среднее по формуле:

.

Для рассматриваемого примера имеем:

Теперь произведем расчет остальных вспомогательных величин:

Номер региона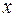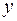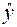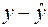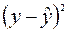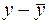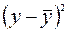
19,76	8,24	67,89	2,76	7,60
2,4	21,3	22,75	-1,45	2,11	-3,94	15,55
2,1	20,51	0,49	0,24	-4,24	18,00
2,6	23,3	24,25	-0,95	0,90	-1,94	3,77
1,7	15,8	17,52	-1,72	2,95	-9,44	89,17
2,5	21,9	23,50	-1,60	2,56	-3,34	11,17
2,4	22,75	-2,75	7,57	-5,24	27,49
2,6	24,25	-2,25	5,04	-3,24	10,52
2,8	23,9	25,74	-1,84	3,39	-1,34	1,80
2,6	24,25	1,75	3,08	0,76	0,57
2,6	24,6	24,25	0,35	0,13	-0,64	0,41
2,5	23,50	-2,50	6,24	-4,24	18,00
2,9	26,49	0,51	0,26	1,76	3,09
2,6	24,25	-3,25	10,54	-4,24	18,00
2,2	21,26	2,74	7,53	-1,24	1,54
2,6	24,25	-0,25	0,06	-1,24	1,54
3,3	31,9	29,48	2,42	5,86	6,66	44,32
3,9	33,96	-0,96	0,93	7,76	60,17
35,4	34,71	0,69	0,47	10,16	103,17
3,7	32,47	1,53	2,34	8,76	76,69
3,4	30,23	0,77	0,60	5,76	33,14
Сумма	57,4	530,1	130,68	545,73

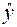
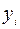
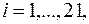
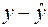
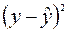
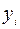
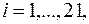
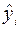
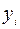
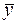
Здесь столбец « » – это значения , рассчитанные с помощью построенного уравнения регрессии, столбцы « » и – это столбцы, так называемых, «остатков»: разностей между исходными значениями , и рассчитанными с помощью уравнения регрессии , а также их квадратов, а в последних двух столбцах – разности между исходными значениями , выборочным средним , а также их квадраты.

Для вычисления коэффициента детерминации воспользуемся формулой ( ):

Значение коэффициента детерминации позволяет сделать предварительный вывод о том, что у нас имеются основания использовать модель линейной регрессии в данной задаче, поскольку .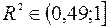

Построим линию регрессии на корреляционном поле, для чего добавим на координатной плоскости точки, соответствующие уравнению регрессии ( ).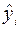

Нанесем теперь уравнение регрессии на диаграмму, используя специальные средства Excel. Для этого необходимо выделить правой кнопкой мыши исходные точки и выбрать опцию Добавить линию тренда.

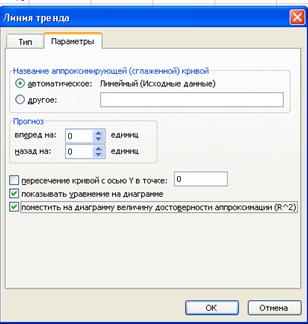
В открывшемся меню Параметры линии тренда выбрать Линейную аппроксимацию. Далее поставить флажок напротив полей Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации .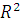

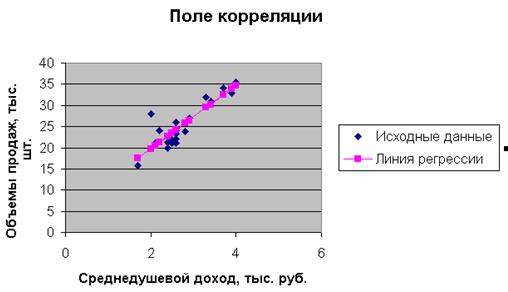
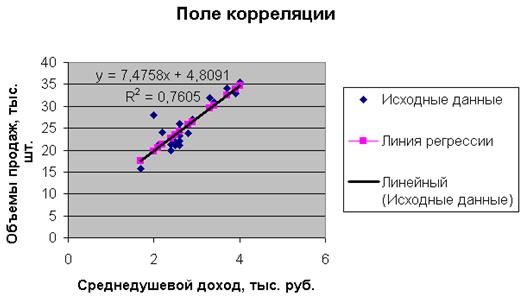
Нажав на ОК, получаем еще одну прямую на диаграмме, которая совпадает с построенными ранее точками линии регрессии:

Сплошная черная линия на диаграмме – это линия регрессии, рассчитанная средствами Excel. Линия регрессии, построенная нами ранее, совпала с данной линией регрессии. Нетрудно убедиться, что уравнение регрессии и коэффициент детерминации тоже совпадают с полученными ранее вручную.

Найдем теперь среднюю ошибку аппроксимации для оценки погрешности модели. Для этого нам потребуется вычислить еще ряд промежуточных величин:

Номер региона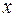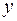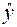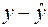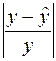
19,76	8,24	0,29
2,4	21,3	22,75	-1,45	0,07
2,1	20,51	0,49	0,02
2,6	23,3	24,25	-0,95	0,04
1,7	15,8	17,52	-1,72	0,11
2,5	21,9	23,50	-1,60	0,07
2,4	22,75	-2,75	0,14
2,6	24,25	-2,25	0,10
2,8	23,9	25,74	-1,84	0,08
2,6	24,25	1,75	0,07
2,6	24,6	24,25	0,35	0,01
2,5	23,50	-2,50	0,12
2,9	26,49	0,51	0,02
2,6	24,25	-3,25	0,15
2,2	21,26	2,74	0,11
2,6	24,25	-0,25	0,01
3,3	31,9	29,48	2,42	0,08
3,9	33,96	-0,97	0,03
35,4	34,71	0,69	0,02
3,7	32,47	1,53	0,05
3,4	30,23	0,77	0,02

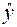
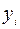
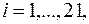
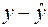
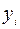
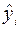
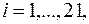
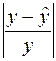
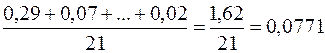
Здесь столбец « » – это значения , рассчитанные с помощью построенного уравнения регрессии, столбец « » – это столбец так называемых «остатков»: разностей между исходными значениями , и рассчитанными с помощью уравнения регрессии , и, наконец, последний столбец « » – это вспомогательный столбец для вычисления элементов суммы по формуле ( ). Просуммируем теперь элементы последнего столбца и разделим полученную сумму на 21 – общее количество исходных данных:

.

Переведем это число в проценты и запишем окончательное выражение для средней ошибки аппроксимации:

.

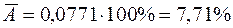
Итак, средняя ошибка аппроксимации оказалась около 8%, что говорит о небольшой погрешности построенной модели. Данную модель, с учетом неплохих характеристик ее качества, вполне можно использовать для прогноза – одной из основных целей эконометрического анализа. Предположим, что среднедушевой месячный доход в одном из регионов составит 4,1 тыс. руб. Оценим, каков будет уровень продаж телевизоров в этом регионе согласно построенной модели? 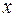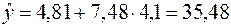Для этого необходимо выбранное значение фактора подставить в уравнение регрессии ( ):

(тыс. руб.),

т.е. при таком уровне дохода, розничная продажа телевизоров составит, в среднем, 35 480 телевизоров.

Источник