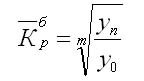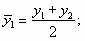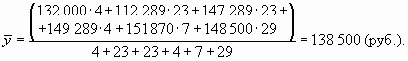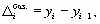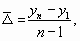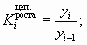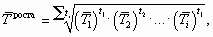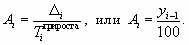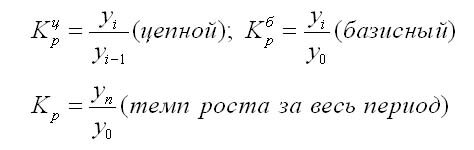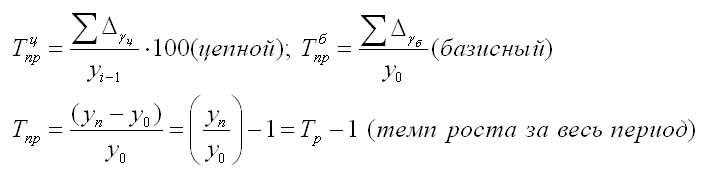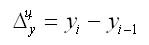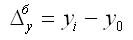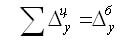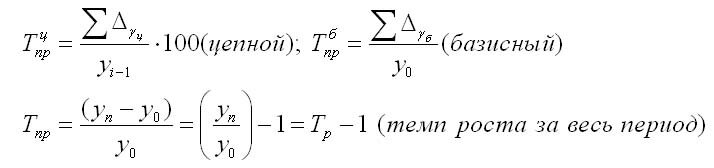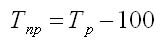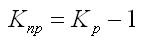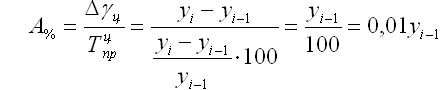средний коэффициент роста что показывает
Средние показатели динамики: уровень ряда, абсолютный прирост, темп роста
Средний уровень ряда в статистике
Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.
Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:
1. При равных интервалах используют среднюю арифметическую простую:
где у — абсолютные уровни ряда;
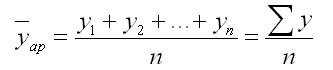
n — число уровней ряда.
2. При неравных интервалах используют среднюю арифметическую взвешенную:
где у1,…,уn — уровни ряда динамики;
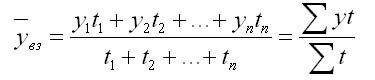
t1,… tn — веса, длительность интервалов времени.
Средний уровень моментного ряда динамики рассчитывается по формуле:
1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:
где у1,…,уn — уровни периода, за который делается расчет;
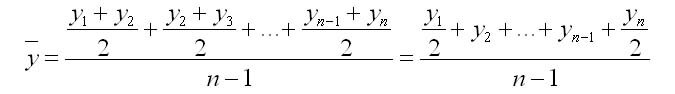
n — число уровней;
n-1 — длительность периода времени.
2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:
где у1,…,уn — уровни рядов динамики;
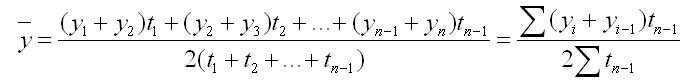
t — интервал времени между смежными уровнями
Средний абсолютный прирост в задачах статистики
Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:
1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:
где n — число степенных абсолютных приростов в исследуемом периоде.
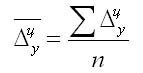
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов
где m — число уровней ряда динамики в исследуемом периоде, включая базисный.
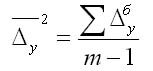
Средний темп роста
Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.
Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:
где n — число цепных коэффициентов роста;
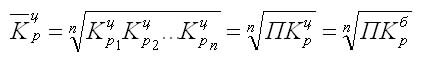
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.
Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.
Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:
Средний темп прироста
Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:
Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
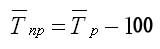
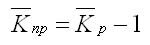
Ряды динамики в статистике
9.2. Показатели ряда динамики
При анализе динамического ряда рассчитываются следующие показатели:
Средние показатели представляют собой обобщенные характеристики ряда динамики. С их помощью сравнивают интенсивность развития явления по отношению к различным объектам, например по странам, отраслям, предприятиям и т.д., или периодам времени.
9.2.1. Средний уровень ряда динамики
Методика расчета среднего уровня зависит от вида динамического ряда, а именно: является ли он моментным или интервальным, с равными или неравными временными промежутками между соседними датами.
Если дан интервальный ряд динамики абсолютных или средних величин с равными периодами времени, то для расчета среднего уровня применяется формула средней арифметической простой:
Пример 9.2. По данным таблицы определим среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект за полугодие:
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь |
|---|---|---|---|---|---|---|
| Средний размер выплаченного страхового возмещения, тыс. руб | 106 | 108 | 108 | 111 | 110 | 112 |
Если временные промежутки интервального динамического ряда неравны, то значение среднего уровня находят по формуле средней арифметической взвешенной, в которой в качестве весов используют длину временных периодов, соответствующих уровням ряда динамики (ti)
Пример 9.3. По данным, представленным в таблице, определим среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект:
| Месяц | Январь | Февраль | Март | II квартал | III квартал | IV квартал |
|---|---|---|---|---|---|---|
| Средний размер выплаченного страхового возмещения, тыс. руб. | 106 | 110 | 138 | 150 | 160 | 140 |
В моментных рядах динамики с одинаковыми временными промежутками между датами средний уровень ряда рассчитывается по формуле средней хронологической простой
Пример 9.4. По приведенным ниже данным о размере денежных средств на счете вкладчика на начало каждого месяца определим средний размер вклада в I квартале 2006 г.:
| Дата | 01.01.06 | 01.02.06 | 01.03.06 | 01.04.06 |
|---|---|---|---|---|
| Остаток денежных средств, руб. | 132 000 | 147 289 | 151 870 | 148 500 |
Средний уровень моментного ряда динамики равен:
Хотя I квартал включает три месяца (январь, февраль, март), в расчете должны быть использованы четыре уровня ряда (включая данные на 1 апреля). Это легко доказать. Действительно, если исчислять средние уровни по месяцам, то получим:
в январе 
в феврале 
в марте 
Рассчитанные средние образуют интервальный ряд динамики с равными временными промежутками, в котором средний уровень исчисляется, как мы видели выше, по формуле средней арифметической простой:
В моментных рядах динамики с неравными промежутками между датами для определения среднего уровня применяется формула средней хронологической взвешенной:
Пример 9.5. По данным о запасах товаров на начало месяца определим средний размер товарных запасов в 2006 г.
| Дата | 01.01.06 | 01.02.06 | 01.03.06 | 01.07.06 | 01.09.06 | 01.12.06 | 01.01.07 |
|---|---|---|---|---|---|---|---|
| Запасы товаров, тыс. руб. | 1 320 | 1 472 | 1 518 | 1 300 | 1 100 | 1 005 | 920 |
Средний уровень ряда равен:
Расстояние между датами
Если имеется полная информация о значениях моментного статистического показателя на каждую дату, то среднее значение этого показателя за весь период исчисляется по формуле средней арифметической взвешенной:
Если мы дополним пример 9.4 информацией о датах изменения денежных средств на счете вкладчика в I квартале 2006 г., то получим:
| Длина периода, дней | 4 | 23 | 23 | 4 | 7 | 29 |
|---|---|---|---|---|---|---|
| Остаток денежных средств, руб. | 132 00 | 112 289 | 147 289 | 149 289 | 151 879 | 148 500 |
По формуле средней арифметической взвешенной находим значение среднего уровня ряда
Как видим, среднее значение отличается от полученного в примере 9.4, оно является более точным, так как в вычислениях использовалась более точная информация. В примере 9.4 были известны лишь данные на начало каждого месяца, при этом не оговаривалось, когда же именно происходили изменения показателя, была применена формула хронологической средней.
В заключение отметим, что расчет среднего уровня ряда теряет свой аналитический смысл в случаях большой изменяемости показателя внутри ряда, а также при резкой смене направления развития явления.
9.2.2. Показатели абсолютного изменения уровней динамического ряда
Абсолютные приросты рассчитываются как разность между двумя значениями соседних уровней динамического ряда (цепные приросты) или как разность между значениями текущего уровня и уровня, принятого за базу сравнения (базисные приросты). Показатели абсолютного прироста имеют те же единицы измерения, что и уровни динамического ряда. Они показывают, на сколько единиц изменился показатель при переходе от одного момента или периода времени к другому.
Базисные абсолютные приросты рассчитывают по формуле
Формула для определения цепных абсолютных приростов имеет вид
Средний абсолютный прирост показывает, на сколько единиц в среднем ежемесячно, или ежеквартально, или ежегодно и т.д. изменялось значение показателя в течение рассматриваемого периода времени. В зависимости от того, какими данными мы располагаем, его можно рассчитать следующими способами:
— цепные абсолютные приросты показателя;
Пример 9.6. По данным таблицы определим показатели абсолютных приростов размера страхового возмещения, выплаченного страховой компанией.
 |
* Сумма всех рассчитанных цепных абсолютных приростов дает базисный абсолютный прирост последнего периода.
Среднемесячный абсолютный прирост за полугодие равен
Таким образом, в среднем ежемесячно размер выплат страхового возмещения увеличивался на 1,2 тыс. руб.
9.2.3. Показатели относительного изменения уровней динамического ряда
Характеристиками относительного изменения уровней ряда динамики являются коэффициенты и темпы роста значений показателя и темпы их прироста.
Так же, как и абсолютные приросты, коэффициенты и темпы роста могут быть цепными и базисными.
Цепные коэффициент и темп роста измеряют относительное изменение текущего уровня показателя по сравнению с предшествующим ему уровнем:
Базисные коэффициент и темп роста характеризуют относительное изменение текущего уровня показателя по сравнению с базисным (чаще всего с первым) уровнем:
Цепные и базисные коэффициенты роста имеют между собой следующую связь:
Средние темп роста и коэффициент роста в динамических рядах с равноотстоящими уровнями рассчитываются по формуле средней геометрической простой
— цепные коэффициенты роста;
— цепные темпы роста.
Эти формулы могут быть приведены к следующему виду:
Для того чтобы определить, на сколько процентов текущий уровень показателя больше или меньше значения предшествующего или базисного уровня, рассчитываются темпы прироста. Они исчисляют путем вычитания 100% из соответствующих темпов роста:
Средний темп прироста рассчитывается аналогичным образом: из среднего темпа роста вычитаются 100%:
Пример 9.7. В таблице приведены рассчитанные коэффициенты роста, темпы роста и прироста показателя, характеризующего среднемесячный размер выплаченного компанией страхового возмещения за период с января по июнь.
| Месяц | Средний размер выплаченного страхового возмещения, тыс. руб., yi | Коэффициент роста | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, тыс. руб. | |||
|---|---|---|---|---|---|---|---|---|
| цепные | базисные | цепные | базисные | цепные | базисные | |||
| Январь | 106 | — | 1 | — | 100 | — | — | — |
| Февраль | 108 | 1,019 | 1,019 | 101,9 | 101,9 | 1,9 | 1,9 | 1,06 |
| Март | 108 | 1,000 | 1,000 | 100,0 | 101,9 | 0 | 1,9 | 1,08 |
| Апрель | 111 | 1,028 | 1,047 | 102,8 | 104,7 | 2,8 | 4,7 | 1,08 |
| Май | 110 | 0,991 | 1,038 | 99,1 | 103,8 | -0,9 | 3,8 | 1,11 |
| Июнь | 112 | 1,018 | 1,057 | 101,8 | 105,7 | 1,8 | 5,7 | 1,10 |
По формуле средней геометрической простой определим среднемесячный коэффициент роста показателя за период с февраля по июнь:
Средний темп роста, соответственно, равен 101,1%. Следовательно, в среднем ежемесячно размер выплат страхового возмещения увеличивался в 1,011 раза, или на 1,1%.
Если известны средние темпы (или коэффициенты) роста за некоторые неравные отрезки времени, то средний темп роста за весь период исчисляется по формуле средней геометрической взвешенной:
Для более полного анализа динамики расчет цепных показателей роста и прироста уровней динамического ряда часто сопровождаются указаниями абсолютных значений 1% прироста.
Абсолютное значение 1% прироста (Аi) определяется как отношение значения абсолютного прироста показателя к его темпу прироста в i-й момент времени:
В последней графе таблицы примера 9.7 рассчитаны цепные абсолютные значения 1% прироста.
Показатели динамики: темп роста и темп прироста
Темп роста
Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр). Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.
Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста
Коэффициент роста может быть рассчитан по формулам:
Также темп роста может определяться так:
Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.
Абсолютный прирост
Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:
1. Абсолютный прирост (цепной):
2. Абсолютный прирост (базисный):
где уi — уровень сравниваемого периода;
Уi-1 — Уровень предшествующего периода;
У0 — уровень базисного периода.
Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:
Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.
Темп прироста
Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:
Темп прироста можно получить из темпа роста:
Коэффициент прироста может быть получен таким образом:
Абсолютное значение 1%-го прироста
Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:
Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.
Примеры расчетов показателей динамики
Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики
О показателях динамики
При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.
Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста. Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения. Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.
Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем. В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными. Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.