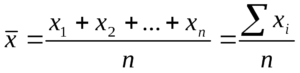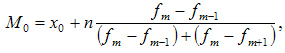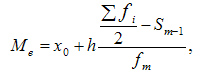среднее значение и среднее арифметическое в чем разница
Как правильно вычислить среднее значение?
Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.
В чем проблема?
Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.
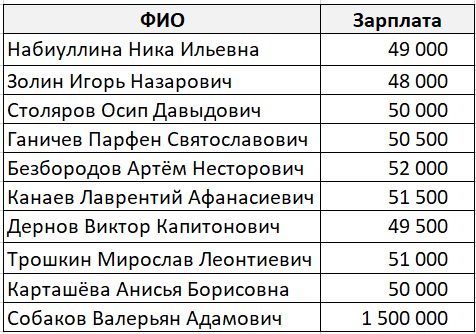
Давайте обратимся к классическому примеру со средней зарплатой.
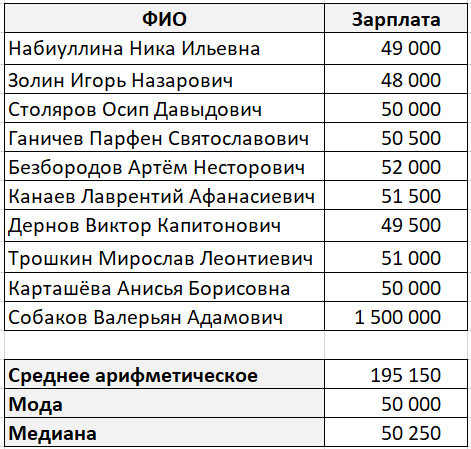
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
И вот какие значения у нас получились:
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
И чтобы ее использовать достаточно написать вот такой запрос:
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
Вычисляем медиану на SQL
Выглядит все это так:
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Какой способ все-таки использовать?
Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.
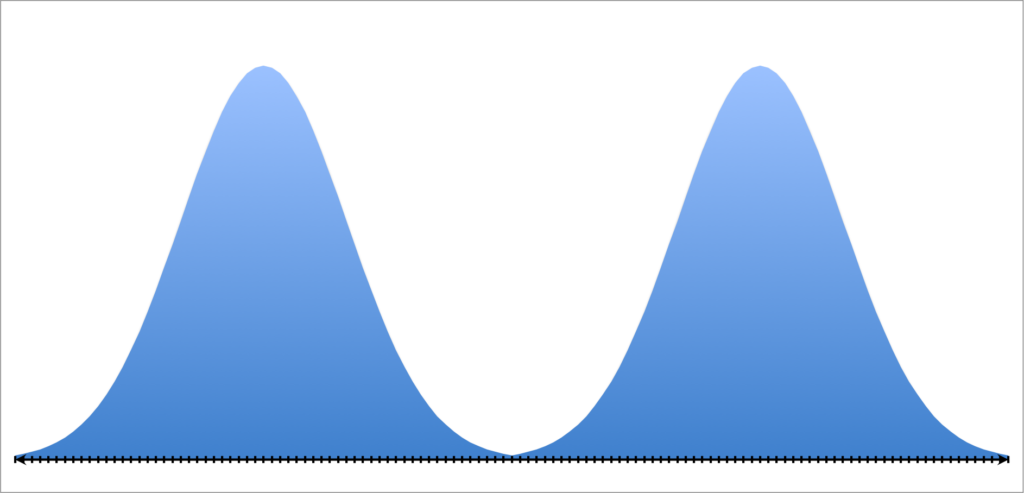
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:
На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.
В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.
А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.
Вывод:
При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.
Окончательный выбор меры центральной тенденции всегда лежит на аналитике.
Среднее значение и среднее арифметическое в чем разница
Сравнение погрешностей приборов критерием Манна-Уитни на сервисе Статзиллы показало, что средний уровень погрешностей двух приборов статистически значимо различается (уровень статистической значимости р=0,02). При этом, среднее арифметическое ошибки прибора А равно 14,6 мм.рт.ст., но и у прибора Б оно также составило 14,6 мм.рт.ст…Какой из приборов статистически лучше?
Ниже приведены результаты расчета значимости различий по Манну-Уитни:
Во-вторых, медиана оценивает среднее, нивелировав влияние выбросов. Но именно эта «сдержанность» медианы может скрыть из виду важные моменты, тогда как среднее арифметическое, завысив или занизив среднее, поможет обратить на них внимание. Так, в нашем примере 2 с погрешностью прибора, медиана говорит, что прибор Б измеряет давление в среднем точнее. Но высокое среднее арифметическое и сами данные указывают на внушительные выбросы – 30 и 90 мм.рт.ст. Очень важно разобраться с ними и понять, чем вызваны такие аномально высокие ошибки измерений.
В-третьих, что бы вы ни решили использовать, обязательно укажите, насколько эта оценка среднего уровня устойчива. Для этого можно использовать различные показатели: корень из дисперсии, ошибку среднего, квартили, минимум и максимум, доверительный интервал. Только совокупность описательных статистик даст полную картину о рассматриваемом показателе и позволит избежать нелепых ошибок, неверных выводов, страшных вопросов на защите и насмешек коллег 🙂
Среднее арифметическое: физический смысл и визуализация
Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.
Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.
Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.
Среднее арифметическое двух чисел
Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:
Их среднее арифметическое:
Физический смысл среднего арифметического
Изобразим два исходных числа и их среднее арифметическое на числовой оси:
Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.
В механике момент силы – это произведение силы F на расстояние l:
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l1 и l2, получим:
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:
Обозначив m координату точки опоры весов, получим:
Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:
Координата опоры весов m:
Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.
Визуальное восприятие равновесия
Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.
Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.
Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.
Математическое ожидание случайной величины
Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:
Теперь точка опоры весов в равновесии это μ:
Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:
Это и есть формула математического ожидания.
Гистограмма
Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.
На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.
Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:
Дайте мне точку опоры, и я переверну Землю. Архимед
Talkin go money
Мода, размах, среднее арифметическое, медиана (Декабрь 2021).
Table of Contents:
Среднее арифметическое представляет собой сумму ряда чисел, деленную на счетчик этой серии чисел.
Если вас попросили найти среднее (среднее арифметическое) количество баллов для тестов, вы просто добавили бы все тестовые баллы учащихся, а затем разделили бы эту сумму на количество студентов. Например, если пять студентов сдавали экзамен, а их баллы составляли 60%, 70%, 80%, 90% и 100%, средний арифметический класс составлял 80%.
Это будет рассчитано как: (60% + 70% + 80% + 90% + 100%) ÷ 5 = 80%.
Причина, по которой вы используете среднее арифметическое для тестов, состоит в том, что каждый результат теста является независимым событием. Если один из учеников плохо справляется с экзаменом, шансы следующего ученика на беду (или хорошо) на экзамен не будут затронуты. Другими словами, оценка каждого учащегося не зависит от оценок других учеников. Однако есть некоторые примеры, особенно в мире финансов, где среднее арифметическое не является подходящим методом для вычисления среднего.
Однако, когда дело доходит до ежегодных инвестиций, цифры не зависят друг от друга. Если вы потеряете тонну денег один год, у вас есть гораздо меньше капитала для получения прибыли в последующие годы, и наоборот. Из-за этой реальности нам нужно вычислить геометрическое среднее из ваших инвестиций, чтобы получить точное измерение того, каков ваш фактический среднегодовой доход за пятилетний период.
Может показаться странным, почему геометрические средние прибыли более точны, чем среднеарифметические доходы, но посмотрите на это следующим образом: если вы потеряете 100% своего капитала за один год, у вас нет никакой надежды сделать вернуть его в течение следующего года. Другими словами, доходность инвестиций не зависит друг от друга, поэтому они требуют, чтобы среднее геометрическое представляло их среднее значение.
Являются экспоненциальными скользящими средними, более эффективными, чем простые или взвешенные скользящие средние?
Узнать о различных типах скользящих средних, а также скользящих средних кроссоверах и понять, как они используются в техническом анализе.
Каковы основные различия между расходимостью конвергенции скользящего среднего (MACD) и экспоненциальными скользящими средними (EMA)?
Понимают экспоненциальную скользящую среднюю или EMA, а также расходимость конвергенции скользящих средних или MACD и их соответствующие цели в качестве технических индикаторов.
В чем разница между конвертирующими средними конвертами и полосами Боллинджера®?
Читал о различиях в том, как строятся полосы Боллинджера и скользящие средние конверты и что это означает для их диапазонов верхних / нижних диапазонов.
8.3. Средние величины в статистике
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
Таблица 8.2 – Результаты опроса работников офиса