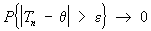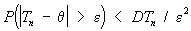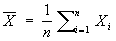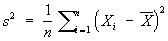состоятельность оценки означает что чем меньше объем выборки тем больше
Состоятельная оценка
Полезное
Смотреть что такое «Состоятельная оценка» в других словарях:
Состоятельная оценка — в математической статистике это точечная оценка, сходящаяся по вероятности к оцениваемому параметру. Содержание 1 Определения 2 Свойства 3 … Википедия
СОСТОЯТЕЛЬНАЯ ОЦЕНКА — сокращенный вариант термина лсостоятельная последовательность оценок … Математическая энциклопедия
ОЦЕНКА СТАТИСТИЧЕСКАЯ — функция от случайных величин, применяемая для оценки неизвестных параметров теоретич. распределения вероятностей. Методы теории О. с. служат основой современной теории ошибок; обычно в качестве неизвестных параметров выступают измеряемые физич.… … Математическая энциклопедия
ОЦЕНКА СОСТОЯТЕЛЬНАЯ — СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ … Социология: Энциклопедия
Пробит-регрессия — (пробит модель, англ. probit) применяемая в различных областях (эконометрика, токсикология и др.) статистическая (нелинейная) модель и метод анализа зависимости качественных (в первую очередь бинарных) переменных от множества… … Википедия
Точечная оценка и ее свойства
Когда оценка определяется одним числом, она называется точечной оценкой. Точечная оценка, как функция от выборки, является случайной величиной и меняется от выборки к выборке при повторном эксперименте.
К точечным оценкам предъявляют требования, которым они должны удовлетворять, чтобы хоть в каком-то смысле быть «доброкачественными». Это несмещённость, эффективность и состоятельность.
Интервальные оценки определяются двумя числами – концами интервала, который накрывает оцениваемый параметр. В отличие от точечных оценок, которые не дают представления о том, как далеко от них может находиться оцениваемый параметр, интервальные оценки позволяют установить точность и надёжность оценок.
В качестве точечных оценок математического ожидания, дисперсии и среднего квадратического отклонения используют выборочные характеристики соответственно выборочное среднее, выборочная дисперсия и выборочное среднее квадратическое отклонение.
Выборочное среднее арифметическое 

Это означает, что эффективная оценка обладает минимальным рассеиванием относительно истинного значения параметра. Заметим, что эффективная оценка существует не всегда, но из двух оценок обычно можно выбрать более эффективную, т.е. с меньшей дисперсией. Например, для неизвестного параметра a нормальной генеральной совокупности N(a,σ) в качестве несмещенной оценки можно взять и выборочное среднее арифметическое, и выборочную медиану. Но дисперсия выборочной медианы примерно в 1.6 раза больше, чем дисперсия среднего арифметического. Поэтому более эффективной оценкой является выборочное среднее арифметическое.
Несмещенные, эффективные и состоятельные оценки



Тема: Статистические оценки
Лекция 1
1. Несмещенные, эффективные и состоятельные оценки.
2. Выборочная средняя и выборочная дисперсия.
3. Анализ смещенности выборочной средней и выборочной дисперсии.
4. Начальный и центральный эмпирические моменты.
5. Число степеней свободы
Несмещенные, эффективные и состоятельные оценки
Одной из центральных задач математической статистики является задача оценки теоретического распределения случайной величины на основе выборочных данных. При этом предполагается, что закон распределения генеральной совокупности известен, но неизвестны его параметры, такие, например, как математическое ожидание, дисперсия. Требуется найти приближенные значения этих параметров, т.е. получить их статистические оценки.
Чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.
Обозначим через 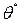
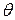
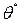
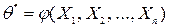
Это значит, что оценка тоже является случайной величиной.
Если для оценки некоторого параметра 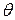
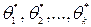
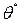
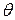
Несмещенной называется статистическая оценка 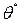
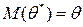
Смещенной называется статистическая оценка 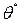
Так же как и для любой случайной величины, оценка 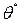
Эффективной называется статистическая оценка 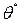
В некоторых случаях становится интересным поведение оценки при неограниченном увеличении объема выборки.
Состоятельной называется статистическая оценка 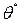
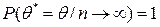
В частности, если дисперсия оценки при 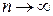
Состоятельность оценки означает что чем меньше объем выборки тем больше
В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки. [c.43]
Тогда Зс и w — несмещенные, состоятельные и эффективные (для нормально распределенной генеральной совокупности) оценки соответственно математического ожидания а и вероятности р, a s2 — смещенная, но состоятельная оценка дисперсии ст2. [c.44]
Как было отмечено в 7.1, b — несмещенная и состоятельная оценка параметра р для обобщенной линейной модели множественной регрессии следовательно, и в частном случае, когда мо- [c.156]
На практике, однако, значения о/ почти никогда не бывают известны. В этом случае при нахождении переменных в формуле (7.27) значения а, следует заменить их состоятельными оценками с,. [c.165]
Если исходить из предположения (7.20), то состоятельными оценками ст являются объясненные (прогнозные) значения el [c.165]
Они позволяют построить состоятельную оценку параметра р модели (8.1). Такая оценка имеет вид [c.196]
Уравнение (8.39) представляет собой уравнение ADL порядка (0,1) и может быть оценено нелинейным методом наименьших квадратов после обратного преобразования Койка. Заметим, впрочем, что состоятельные оценки параметров уравнения (8.39) можно получить и обычным методом наименьших квадратов, так как в уравнении объясняющая переменная Yf не коррелирует со значением случайного члена е в момент времени t (см. 8.1). [c.207]
В рассмотренном примере уравнения (9.6) были однозначно разрешимы относительно исходных параметров, что позволило найти их состоятельные оценки. Очевидно, что такая ситуация имеет место не всегда. Рассмотрим эту проблему более подробно. [c.230]
Степень реалистичности доверительных интервалов параметров регрессии обеспечивается, если оценки будут не только несмещенными и эффективными, но и состоятельными. Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии 6, имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице. [c.156]
Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей и четвертой предпосылок. [c.160]
Таким образом, разность 04 — будет сколь угодно малой, а предел стремится к единице при увеличении объема выборки при 6 > 0. Свойство очевидно, так как чем ближе п к >, тем ближе оценка ь к 0. Отсюда следует, что состоятельность оценки возрастает с увеличением объема выборки. [c.45]
Если удастся построить АКМ4-модель для ряда остатков, то можно получить эффективные оценки параметра р, а также несмещенные и состоятельные оценки дисперсий р с помощью обобщенного метода наименьших квадратов. Мы рассмотрим эту процедуру на простейшей (и в то же время наиболее часто встречающейся) авторегрессионной модели первого порядка. [c.181]
Оказывается, если ряды xt и yt на самом деле являются коинтегрируемыми, то состоятельная оценка параметра (3 получается как оценка обычного метода наименьших квадратов, примененного к модели [c.221]
Заметим, что проблема сверхидентифицируемости — это проблема количества наблюдений с увеличением объема выборки все различные состоятельные оценки параметра стремятся к одному и тому же истинному значению. Между тем проблема неидентифицируемости — это проблема структуры модели. Неидентифицируемость не исчезает с ростом количества наблюдений и означает, что существует бесконечное число структурных моделей, имеющих одну и ту же приведенную форму. [c.232]
В практических задачах полезно иметь в виду, что матрица n- lo ztAn (см. (12.19)) является состоятельной оценкой матрицы А. [c.369]