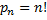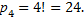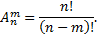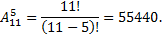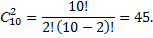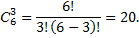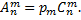сочетание и размещение в чем разница комбинаторика

Разница между сочетанием и размещением

Б. Паскаль и Ферма, изучая теорию азартных игр, были основателями нового раздела математики, называемого комбинаторикой. В ней изучается, какое количество комбинаций заданного типа можно составить из предложенных элементов.

Определение

Сочетания — соединения, каждое из которых составлено из k1 элементов, выбранных из n1 различных элементов, состав которых отличается хотя бы на один элемент.

Размещения — cоединения, каждое из которых составлено из k1 элементов, взятых из n1 различных элементов, у которых состав элементов или их порядок отличают их друг от друга.

Сравнение

Сочетания — соединения, содержащие k1 элементов, выбранных из n1 различных элементов. Сочетания отличаются друг от друга хотя бы на один элемент. Порядок следования элементов не важен. Число сочетаний равно n1 элементов.

Наборы, которых отличает только порядок следования элементов, но не состав, считаются одинаковыми. Отличие сочетаний друг от друга составом, но не порядком следования элементов.

Пример. Сочетание — нужно выбрать 3 предмета из 6. Есть предметы с номерами от 1 до 6. Выбираем из этого набора предметы в любом порядке с номерами 1, 4 и 6. Это и есть сочетание.

Размещениями называют соединения, каждое из которых содержит k1 элементов, взятых из n1 различных элементов, которых отличает друг от друга порядок или состав элементов. В размещениях не должно быть дубликатов.

Источник

Сочетания и размещения — что это такое и в чем разница

Оба этих понятия – сочетание и размещение – относятся к науке комбинаторике. Это раздел математики, созданный учеными Б. Паскалем и П. Ферма в процессе исследования теории карточных игр. Комбинаторика используется в решении задач особенного рода: когда требуется вычислить количество потенциальных вариантов для какой-либо ситуации. Примером может служить подсчет возможных позиций на шахматной доске после первого хода «черных» и «белых».

О сочетании и размещении говорят, когда из множества необходимо выбрать какое-либо подмножество. Понятия эти весьма близки по своему смыслу, поэтому так трудно бывает понять разницу между ними. Но она существует (причем принципиальная!). Ниже об этом достаточно простым языком написано в статье.

Сочетания

Сочетание – это подмножество, состоящее из К элементов, выбранных из множества, включающего в себя N элементов. При этом выполняется такое условие: N > К.

Важный момент: порядок расположения в данной выборке никакого значение не имеет. То есть комбинации, отличающиеся порядком размещения элементов, но не составом, считаются одинаковыми сочетаниями.

Образно проиллюстрировать понятие можно на примере лотереи. Предположим, человеку предлагается угадать 3 выпавшие цифры из 15-ти. Он выбрал следующий набор – 1, 6, 10. И уже не важно, в каком порядке они выпадут: 1, 6, 10; 1, 10, 6; 10, 1, 6; 10, 6, 1; 6, 10, 1; 6, 1, 10. Главное – состав комбинации. Если он совпадает с загаданным накануне набором цифр, игрок считается победителем.

Сочетания обозначаются следующим образом: С К _N. Где N – количество элементов в множестве, а К – количество объектов в производимой выборке. Для нашего примера N = 15, а К = 3.

Существует формула для определения числа возможных сочетаний в множестве. Выглядит она так: N!/((N-K)!*K!) подставим цифры из нашего примера:

Это означает, что из 15 чисел можно составить 455 различных комбинаций, включающих в себя три разных числа.

Такие подсчеты в нашем примере позволяют определить велики ли шансы субъекта на выигрыш.

Размещения

В самом названии этого термина присутствует корень, позволяющий понять его суть. Размещение – тоже подмножество, выбранное из первоначального множества. Но здесь уже существенное значение имеет место расположения элемента в комбинации. То есть если сочетания могут различаться только составом объектов, то размещения разнятся и составом, и порядком следования элементов.

Получается, что количество размещений всегда превосходит число сочетаний, при условии выборки из одного и того же множества.

Это легко проследить, если сделать выборку трех элементов из множества, состоящего всего из 4 объектов (от 1-го до 4-х).

Сочетаний здесь будет всего 4 (это легко проверить и по приведенной выше формуле):

Размещений же окажется гораздо больше:

123, 132, 321, 312, 231, 213, 234, 243, 324, 342 и т.д.

Существует формула, позволяющая подсчитать возможное количество размещений в представленном множестве:

Для нашего примера посчитаем количество потенциальных размещений:

Получается, что для состоящего из 4-х элементов множества существует 4 сочетания и целых 24 размещения.

Для тех, кто увлекается спортивными ставками, эти знания могут пригодится для того, чтобы рассчитать шансы на выигрыш.

Например, в турнире участвует 6 команд. Необходимо определить количество возможных комбинаций троек призеров кубка.

Обозначим названия команд буквами: А, Б, В, Г, Д, Е.

Сначала определим команду, которая станет золотым призером чемпионата. Таких вариантов, очевидно, 6: А, Б, В, Г, Д, Е.

Затем выбираем один из вариантов (пусть это будет комбинация, в которой золото принадлежит команде А), и определяем для него потенциального серебряного призера. Таких комбинаций уже окажется всего 5, так как одна команда уже записана на 1-м месте: АБ, АВ, АГ, АД, АЕ.

Такую пятерку вариаций можно сформировать для каждой из команд. То есть всего претендентов на серебро оказывается 30 (5*6).

Для каждой двойки первых призеров (чемпион-серебряный призер) можно составить только 4 комбинации с бронзовым призером. Первые два места уже распределены, так что остается 4 команды (6-2). Подберем комбинации для варианта АБ: АБВ, АБГ, АБД, АБЕ.

Мы уже подсчитали выше количество возможных комбинаций для первых двух мест – их оказалось 30. Теперь это число умножаем на 4 – получаем 120.

Выходит, что если в турнире участвует 6 команд, вариантов их размещения по первым трем местам может быть целых 120. Угадать призеров не так просто.

Сочетания и размещения: в чем же разница?

И сочетания, и размещения являются выборкой из определённого множества. Принципиальная разница между понятиями заключается лишь в том, что в случае сочетаний порядок расположения элементов не имеет значения, а в случае размещений он важен. Именно поэтому в пределах одного и того же множества количество сочетаний всегда оказывается меньше числа размещений.

Источник

Основные понятия

Перестановки

Обычно начинают объяснять с размещений, но я сознательно хочу начать с перестановок, так как на их примере проще понять логику вычисления.

Итак, вернемся к задаче из примера: Сколькими способами можно создать числа, переставляя цифры в числе 12345?

У нас есть пять цифр (пусть это будет пять кубиков с цифрами): 1,2,3,4,5.

У нас есть пять, пока еще свободных, позиций под их размещение (пусть это будут пустые коробочки): ▢▢▢▢▢.

Начинаем постепенно заполнять эти позиции: на первую позицию (в первую коробочку) мы можем поместить одну из пяти цифр (один из пяти кубиков). То есть у нас есть пять вариантов заполнения первой позиции.

Предположим, мы взяли кубик с номером 4.

Теперь у нас осталось четыре цифры (кубика): 1,2,3,5.

Позиций (коробочек) у нас осталось пять, но первая уже заполнена, то есть свободных позиций четыре: 4▢▢▢▢.

На размещение во второй коробочке у нас осталось 4 «претендента». Мы взяли кубик с номером 4. Но если бы мы взяли любой из других кубиков, у нас все равно было бы 4 варианта заполнения второй коробочки (просто мы выбирали бы из другого набора ставшихся кубиков), то есть на каждый вариант заполнения первой коробочки у нас приходится по четыре варианта заполнения второй.

Предположим, мы взяли кубик с номером 1.

У нас осталось три цифры (кубика): 2,3,5.

Позиций (коробочек) у нас осталось пять, но первые две уже заполнены: 41▢▢▢.

Почему последние два числа совпадают? Все просто: на последнем этапе у нас остается всего один кубик, но и одна пустая коробочка. То есть у нас уже нет вариантов размещения. Поэтому последний шаг уже не оказывает влияния на число перестановок.

Нетрудно догадаться, что сколько бы элементов (цифр, чисел, воздушных шариков и так далее) нам ни дали, мы можем узнать число из перестановок умножая последовательно число элементов на все целые числа меньше него.

В математике для подобной операции существует функция, которая называется факториал и обознается восклицательным знаком, стоящим за числом, факториал которого нужно вычислить.

Обозначается число перестановок из n так:

В итоге мы получаем следующую формулу для вычисления количества перестановок для n элементов:

Размещения

Размещение очень похоже на перестановку, с одной лишь разницей: у нас обычно «не хватает» позиций (коробочек) для размещения всех элементов (кубиков).

Обозначается размещение n из k так:

При k = n (то есть когда число «коробочек» равно числу «кубиков») количество размещений равно количеству перестановок порядка n.

Возьмем задачу из примера: Сколько трехзначных чисел можно создать из цифр от 1 до 5?

Если мы по аналогии с перестановками попробуем по шагам считать, то увидим, что мы остановились после заполения третьей (последней) «коробочки»:

Мы можем записать так:

а в общем виде так:

Размещение с повторением

Существует вариант, когда мы можем повторно использовать один и тот же элемент, независимо от того, использовали мы его до этого, или нет. В случае с кубиками и коробочками это будет выглядеть так: у нас есть не по одному кубику с каждым номером, а неограниченное число кубиков с каждым из чисел. Это называется размещение n из k с повторением и обозначается:

Начнем заполнять «коробочки».

У нас есть пять кубиков с цифрами: 1,2,3,4,5.

У нас есть пять, пока еще свободных, позиций под их размещение (пусть это будут пустые коробочки): ▢▢▢▢▢.

Положим, в первую мы кладем номер 4.

Значит у нас осталось четыре свободных «коробочки»: 4▢▢▢▢.

Начинаем заполнять вторую коробочку. Их у нас четыре, как я уже сказал. Но кубиков у нас, в отличии от размещения без повторения осталось всё равно пять. Значит у нас на каждый вариант заполения первой коробочки приходится пять вариантов заполения второй.

Соотвественно две первые коробочки мы можем заполнить 5⋅ 5 = 25 способами (а не 5⋅ 4 = 20, как в случае без повторения).

Повторяя рассуждения мы вычислим, что три коробочки мы можем заполнить 5⋅ 5⋅ 5 = 125 способами.

В общем случае число размещений равно числу элементов (кубиков) в степени числа возможных позиций для размещения (коробочек).

Сочетания

Сочетания похожи на размещения, однако для сочетаний совершенно не важно, в каком порядке расположены коробочки. Обозначаются сочетания так:

Как нам вывести формулу для сочетаний? Для начала возьмем число размещений и разделим на число всех вариантов «перемешивания» каждого набора (ведь при «перемешивании» получается тот же набор, просто расположенный в другом порядке). Но чему равно число этих «перемешиваний», спросите вы? А если не спросите, то значит я не зря писал эту статью, потому что внимательный читатель сам заметит, что в данном случае речь идет о перестановках. Обратите внимание, что тут мы переставляем не кубики, а коробочки, которых k штук, поэтому речь идет не о P_n, а о P_k. В итоге мы получаем формулу:

А теперь вернемся к задаче из примера: В вазе есть тюльпаны пяти цветов: белые, желтые, оранжевые, красные и розовые. Сколькими способами можно создать букет из трех тюльпанов, если в букете должно быть по одному цветку каждого цвета?

Сочетания с повторениями

Я думаю, вы уже догадались, что такое сочетания с повторениями. Это сочетания, при которых можно использовать элементы повторно. Обозначается сочетание с повторением так:

А теперь задание для особо внимательных: могли ли мы совершить такой же «фокус» в случае с размещением с перестановками? Если могли, то почему не сделали? А если не могли, то почему? Жду ответов в комментариях.

Ну и пара примеров задач.

Есть гвоздики двух цветов. Нужно собрать букеты из трех цветков так, чтобы у каждого был уникальный набор. Скольким букетов можно собрать?

Есть гвоздики четырех цветов. Нужно собрать букеты из трех цветков так, чтобы у каждого был уникальный набор. Скольким букетов можно собрать?

Проведем аналогию с кубиками и коробочками. Можно преобразовать эту задачу к виду «Нужно разместить шесть кубиков в трех коробочках». И решение:

Источник

Сочетания. Размещения. Перестановки

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

Где ( ).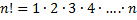

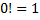
Рассмотрим пример: сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?

.

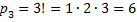
Или такой пример. Порядок выступления семи участников на студенческой конференции определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Решение: каждый вариант жеребьевки отличается только порядком участников, то есть является перестановкой из 7 элементов. Их число находится

.

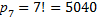
Пример. К кассе за получением денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?

Решение: очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырех человек, их число равно

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо их порядком, либо составом элементов.

Число всех возможных размещений рассчитывается

Пример: сколько можно составить сигналов из 6 флажков различного цвета, взятых по два?

Пример: расписание одного дня состоит из пяти уроков. Определить число вариантов расписания при выборе из 11 дисциплин.

Решение: каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов, как составом дисциплин, так и порядком их следования, то есть является размещением из 11 элементов по 5. Число вариантов расписания находят по формуле

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

Пример: сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Пример: в шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение: каждая партия играется двумя участниками из 16 и отличается только составом пар участников, то есть представляет собой сочетание из 16 элементов по два

Пример: имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать три штамма. Сколькими способами можно это сделать?

Решение: способы отбора считаются различными, если каждый отобранный штамм различается хотя бы одним элементом. Это число

То есть имеется 20 способов.

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

При решении задач комбинаторики используют следующие правила.

Правило суммы: если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно 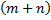способами.

Правило произведения: если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А,В) в указанном порядке может быть выбрана 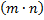способами.

Пример: в студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

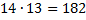
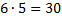
Решение: по правилу умножения двух девушек можно выбрать способами, а двух юношей способами. Следует выбрать двух студентов одного пола: двух девушек или двух юношей. Согласно правилу сложения таких способов выбора будет 182 + 30 = 212.

Контрольные вопросы

1. Что называют графом?

2. Какие вершины графа можно назвать смежными?

3. Возможно ли начертить граф с нечетным числом нечетных вершин?

4. Чем определяется полный граф?

5. Что называют перестановками, размещениями, сочетаниями?

6. Сформулировать правила суммы и произведения.

Источник

Мастер-класс по теме «Элементы комбинаторики: перестановки, сочетания и размещения»

Разделы: Математика

Элементы комбинаторики: перестановки, сочетания, размещения.

“Число, положение и комбинация – три
взаимно пересекающиеся, но различные
сферы мысли, к которым можно
отнести все математические идеи”.
Джозеф Сильвестр (1844 г.)

Оборудование: компьютеры, проектор, экран, презентация, электронные и на бумажных носителях тесты, задачи “Судоку”, кубики Рубика, папки для ВСР (внеаудиторная самостоятельная работа), рабочие тетради, чистые ватманы, калькуляторы, цветная бумага, клей, ножницы, фломастеры.

I. Организационный момент

Сообщение целей и задач занятия: В связи с тем, что по дисциплине “Математика” на 2 курсе специальности “Технология деревообработки” на тему “Основные понятия комбинаторика: перестановки, размещения, сочетания” отводится 2 часа, а рассмотреть нужно много материала, решать задачи, создать проект, вам было выдано задание на внеаудиторную самостоятельную работу следующее: в литературе по истории математики, в энциклопедиях, в учебниках и в интернете найти материал о разделе математики, имеющем звучное название “комбинаторика”. Слайды № 1–2. Презентация

В календарно-тематическом плане по дисциплине “Математика” на 2 курсе специальности “Технология деревообработки” на тему “Основные понятия комбинаторика: перестановки, размещения, сочетания” отводится 2 часа. Изучить теоретический материал, решить задачи разных видов за такой временной промежуток невозможно. Для достижения глубокого изучения материала было выдано задание на внеаудиторную самостоятельную работу: в литературе по истории математики, в энциклопедиях, в учебниках и в интернете найти материал о разделе математики, имеющем звучное название “комбинаторика”. Слайды № 1–2.

Запись даты, темы урока.

II. Работа над темой занятия

Из глубокой древности до современного человечества дошли сведения о том, что уже тогда люди занимались выбором объектов и расположения их в том или ином порядке и увлекались составлением различных комбинаций. Так, например, в Древнем Китае увлекались составлением квадратов, в которых заданные числа располагали так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же (современная игра – задача “Судоку”). Такие задачи вы могли встречать в журналах и газетах. В частности, наша Мариинская газета “Вперед” довольно часто предлагает читателям такие задачи. В Древней Греции подобные задачи возникали в связи c такими играми, как шашки, шахматы, домино, карты и т.д.

Комбинаторика – самостоятельная ветвь математической науки. Cлайд № 3

Как трактует это слово Большой Энциклопедический Словарь?

Комбинаторика – это раздел математики, в котором изучаются простейшие “соединения”: перестановки, размещения, сочетания. Этот раздел иначе называют “комбинаторный анализ”.

Сегодня мы будем рассматривать перестановки, размещения, сочетания, как соединения, как комбинаторные конфигурации.

Разделы комбинаторики: перечислительная, структурная, вероятностная, топологическая – слайд № 5.

Давайте вспомним известное вам из детства сказание о том, как богатырь или другой добрый молодец, доехав до развилки трех дорог, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации. И целый раздел математики, именуемый КОМБИНАТОРИКОЙ, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую – слайд № 6.

Итак, комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Задачей комбинаторики можно считать задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.

Перестановки-соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число их

Количество всех перестановок из n элементов обозначают

Число n при этом называется порядком перестановки – слайд № 7–10.

Необходимо знать, что 0!=1

Термин “перестановки” употребил впервые Якоб Бернулли в книге “Искусство предположений”.

Примеры решения задач:

Задача №1. Сколькими способами 7 книг разных авторов можно расставить на полке в один ряд?

Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок обозначается Рп и оно равно п!, т.е. Рп = п!, где п! = 1 * 2 * 3 * … п.

Решение: Р7 = 7!, где 7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 =5040, значит существует 5040 способов осуществить расстановку книг.

Ответ: 5040 способов.

Задача № 2 (о квартете)

В знаменитой басне Крылова “Квартет” “Проказница мартышка, Осел, Козел да косолапый Мишка” исследовали влияние взаимного расположения музыкантов на качество исполнения.

Зададим вопрос: Сколько существует способов, чтобы рассадить четырех музыкантов?

Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их.

В комбинаторике размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны.

В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы и являются различными, хотя состоят из одних и тех же элементов <1,2,3>(то есть, совпадают как сочетания).

Термин “Размещение” употребил впервые Якоб Бернулли в книге “Искусство предположений”.

Примеры решения задач:

Задача № 1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений.

Размещаются здесь десять цифр по 6. Значит, ответ на выше поставленную задачу будет:

Задача № 2. В группе ТД – 21 обучается 24 студентов. Сколькими способами можно составить график дежурства по техникуму, если группа дежурных состоит из трех студентов?

Ответ: 12144 способа

Сочетания-соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом; число их .

Таким образом, количество вариантов при сочетании будет меньше количества размещений. Cлайды № 14–16.

В комбинаторике сочетанием из n по m называется набор m элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Термин “сочетание” впервые встречается у Блеза Паскаля в 1665 году.

Примеры решения задач:

Задача №1. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?

Решение: Так как кнопки нажимаются одновременно, то выбор этих кнопок – сочетание. Отсюда возможно

Ответ: 120 вариантов.

Задача № 2. Сколько экзаменационных комиссий, состоящих из 3 членов, можно образовать из 10 преподавателей?

Решение: По формуле находим:

комиссий

Ответ: 120 комиссий.

Библиографическая справка – слайд № 17.

Общее у всех этих задач то, что их решением занимается отдельная область математики, называемая комбинаторикой. “Особая примета” комбинаторных задач – вопрос, который всегда можно сформулировать так, чтобы он начинался словами: “Сколькими способами…?”. Cлайд № 18.

3. Решение задач: тексты задач с решениями в приложении 1 – начало на слайде № 19.

4. Исторические сведения о комбинаторике на слайдах № 20–21 (частично даны сведения при изучении темы, остальные данные для проекта студенты возьмут из материалов для ВСР).

5. Связи комбинаторики на слайдах № 22–31 (частично даны сведения при изучении темы, остальные данные для проекта студенты возьмут из материалов для ВСР).

6. Выдвижение гипотезы. Гипотеза – это научное предположение, выдвигаемое для объяснения каких-нибудь явлений, вообще – предположение, требующее подтверждения.

8. Защита проектов: при защите проекта сделать вывод: подтверждает ли проект выдвинутую гипотезу или опровергает.

9. Тестирование: Часть студентов тестируется на компьютерах, остальные – на бумажных носителях по теме занятия. По мере выполнения тестов студенты решают задачу “Судока” или собирают кубик Рубика.

10. При выходе из кабинета каждый студент выбирает прямоугольник по цвету, соответствующему надписями “всё понятно и усвоено”, “трудно и не всё понятно”, “не понятно и не усвоено”, и опускает в соответствующий конверт.

1. Фадеев Д.К., Никулин М.С., Соколовский. Элементы высшей математики для школьников. Москва. “Наука”, 1987 год.

2. Грэхем Р., Кнут Д.А., Паташник О. Конкретная математика.. Москва “Мир”, 1998 г.

3. Богомолов Н.В. Практические занятия по математике: Учеб. Пособие для техникумов, Москва. “Высшая Школа, 1983.

4. Перельман Я.И. “Занимательная алгебра. Занимательная геометрия, Москва, АСТ “Астрель”, 2002 год.

5. Савин А.П. “Энциклопедический словарь юного математика”, Москва “Педагогика”, 1985.

6. Сканави М.И. “Сборник задач по математике для поступающих в вузы”, Москва, “Высшая школа”, 1998 г.

8. Элементы теории вероятностей. Математика. Приложение к газете «Первое сентября», № 41, 42.

10. Лютикас В.С. Факультативный курс по математике: Теория вероятностей, Москва, “ Просвещение”, 1990.

12. Андреева Е. В. “Комбинаторные задачи”, Москва, “Чистые пруды”, 2005 г.

Источник