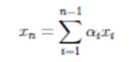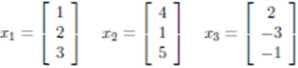след матрицы это что
Линейная алгебра для исследователей данных
«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».
Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.
Произведения векторов
Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy
называется следующее вещественное число:
Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество
Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть
Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:
След обладает следующими свойствами:
Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.
Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.
Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.
Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

Нормы
Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:
Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:
Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).
f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).
Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).
Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)
Другими примерами норм являются норма l₁
Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как
Нормы также могут быть определены для матриц, например норма Фробениуса:
Линейная независимость и ранг
линейно зависимы, так как x₃ = −2xₙ + x₂.
Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.
Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).
Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).
Ортогональные матрицы
Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м
атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.
Непосредственно из определений ортогональности и нормированности следует, что
Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n
для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

Область значений и нуль-пространство матрицы
Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,
Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть
Квадратичные формы и положительно полуопределенные матрицы
Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:
Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как
(или просто A > 0), а множество всех положительно определенных матриц часто обозначают
Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как
(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают
Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной
, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx
), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.
Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что
Собственные значения и собственные векторы
Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство
На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).
Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.
След (линейная алгебра)
СОДЕРЖАНИЕ
Определение [ править ]
Пример [ править ]
Свойства [ править ]
Основные свойства [ править ]
tr ( A + B ) = tr ( A ) + tr ( B ) tr ( c A ) = c tr ( A ) <\displaystyle <\begin

Матрица и ее транспонирование имеют один и тот же след: [2] [3] [4] : 34
Это сразу следует из того, что транспонирование квадратной матрицы не влияет на элементы по главной диагонали.
След продукта [ править ]
Это означает, что след произведения матриц равного размера функционирует аналогично скалярному произведению векторов (представьте, что A и B как длинные векторы со столбцами, наложенными друг на друга). По этой причине обобщения векторных операций на матрицы (например, в матричном исчислении и статистике ) часто включают след матричных произведений.
Для вещественных матриц A и B след продукта также можно записать в следующих формах:
Циклическое свойство [ править ]
Произвольные перестановки не допускаются: как правило,
Однако, если рассматриваются произведения трех симметричных матриц, допускается любая перестановка, поскольку:
где первое равенство связано с тем, что следы матрицы и ее транспонирования равны. Обратите внимание, что в целом это неверно для более чем трех факторов.
След матричного продукта [ править ]
След продукта Кронекера [ править ]
След продукта Кронекера двух матриц является произведением их следов:
Полная характеристика следа [ править ]
Следующие три свойства:
Инвариантность подобия [ править ]
След произведения симметричной и кососимметричной матрицы [ править ]
Связь с собственными значениями [ править ]
След единичной матрицы [ править ]
След идемпотентной матрицы [ править ]
След нильпотентной матрицы [ править ]
Трассировка равна сумме собственных значений [ править ]
В более общем смысле, если
f ( x ) = ∏ i = 1 k ( x − λ i ) d i <\displaystyle f(x)=\prod _
то есть след квадратной матрицы равен сумме собственных значений, подсчитанных с кратностями.
След коммутатора [ править ]
Наоборот, любая квадратная матрица с нулевым следом представляет собой линейную комбинацию коммутаторов пар матриц. [примечание 3] Более того, любая квадратная матрица с нулевым следом унитарно эквивалентна квадратной матрице с диагональю, состоящей из всех нулей.
След эрмитовой матрицы [ править ]
След эрмитовой матрицы действительный, потому что элементы на диагонали действительны.
След матрицы перестановок [ править ]
След матрицы проекции [ править ]
Матрица P X идемпотентна, и, вообще говоря, след любой идемпотентной матрицы равен ее собственному рангу.
Экспоненциальный след [ править ]
След линейного оператора [ править ]
Отношения собственных значений [ править ]
В более общем смысле,
Производные [ править ]
который явно имеет нулевую трассу, что указывает на то, что эта матрица представляет собой бесконечно малое преобразование, сохраняющее площадь.
Приложения [ править ]
Алгебра Ли [ править ]
Фактически, существует внутреннее разложение операторов / матриц прямой суммой на бесследные операторы / матрицы и скалярные операторы / матрицы. Карта проекции на скалярные операторы может быть выражена в терминах следа, в частности, как: g l n = s l n ⊕ K <\displaystyle <\mathfrak
0 → s l n → g l n → tr K → 0 <\displaystyle 0\to <\mathfrak След определяет билинейную форму: Форма является симметричной, невырожденной [примечание 4] и ассоциативной в том смысле, что: Для сложной простой алгебры Ли (такой как n ) каждая такая билинейная форма пропорциональна друг другу; в частности, к форме убийства. s l <\displaystyle <\mathfrak Две матрицы X и Y называются ортогональными по следу, если Для матрицы A размера m × n с комплексными (или действительными) элементами и H, являющимся сопряженным транспонированием, имеем Если K является следовым классом, то для любого ортонормированного базиса след определяется выражением ( φ n ) n <\displaystyle (\varphi _ и конечна и не зависит от ортонормированного базиса. [6] Операция тензорного сжатия обобщает след на произвольные тензоры. К следу можно также подойти безкоординатным образом, т. Е. Без обращения к выбору базиса, следующим образом: пространство линейных операторов в конечномерном векторном пространстве V (определенном над полем F ) изоморфно пространству пространство V ⊗ V ∗ линейным отображением Существует также каноническая билинейная функция t : V × V ∗ → F, которая состоит в применении элемента w ∗ из V ∗ к элементу v из V, чтобы получить элемент из F : можно интерпретировать композиционную карту ( V ⊗ V ∗ ) × ( V ⊗ V ∗ ) → ( V ⊗ V ∗ ) <\displaystyle (V\otimes V^<*>)\times (V\otimes V^<*>)\to (V\otimes V^<*>)> происходит от спаривания V ∗ × V → F на средних членах. Отслеживание следа продукта происходит в результате спаривания на внешних терминах, при взятии продукта в обратном порядке и последующем взятии следа просто выбирается, какое спаривание применяется первым. С другой стороны, взятие следа A и следа B соответствует применению спаривания к левым и правым членам (а не к внутреннему и внешнему) и, таким образом, отличается. В координатах это соответствует индексам: умножение дается на что то же самое, в то время как Если t определено, как указано выше, Далее можно дуализировать эту карту, получив карту Затем можно составить их, F,> Матрица и ее транспонирование имеют одинаковый след: Это сразу следует из того, что транспонирование квадратной матрицы не влияет на элементы по главной диагонали. Это означает, что след произведения матриц равного размера функционирует аналогично скалярному произведению векторов (представьте, что A и B как длинные векторы со столбцами, наложенными друг на друга). По этой причине обобщения векторных операций на матрицы (например, в матричном исчислении и статистике ) часто включают след матричных произведений. Для вещественных матриц A и B след продукта также можно записать в следующих формах: Произвольные перестановки не допускаются: как правило, Однако, если рассматриваются произведения трех симметричных матриц, допускается любая перестановка, поскольку: где первое равенство связано с тем, что следы матрицы и ее транспонирования равны. Обратите внимание, что в целом это неверно для более чем трех факторов. След продукта Кронекера двух матриц является произведением их следов: Следующие три свойства: В более общем смысле, если то есть след квадратной матрицы равен сумме собственных значений, подсчитанных с кратностями. Наоборот, любая квадратная матрица с нулевым следом представляет собой линейную комбинацию коммутаторов пар матриц. Более того, любая квадратная матрица с нулевым следом унитарно эквивалентна квадратной матрице с диагональю, состоящей из всех нулей. След эрмитовой матрицы действительный, потому что элементы на диагонали действительны. Матрица P X идемпотентна, и, вообще говоря, след любой идемпотентной матрицы равен ее собственному рангу. В более общем смысле, который явно имеет нулевую трассу, что указывает на то, что эта матрица представляет собой бесконечно малое преобразование, сохраняющее площадь. Фактически, существует внутреннее разложение операторов / матриц прямой суммой на бесследные операторы / матрицы и скалярные операторы / матрицы. Карта проекции на скалярные операторы может быть выражена в терминах следа, в частности, как: грамм л п знак равно s л п ⊕ K <\ displaystyle <\ mathfrak 0 → s л п → грамм л п → tr K → 0 <\ displaystyle 0 \ to <\ mathfrak След определяет билинейную форму: Форма является симметричной, невырожденной и ассоциативной в том смысле, что: Для сложной простой алгебры Ли (такой как n ) каждая такая билинейная форма пропорциональна друг другу; в частности, к форме убийства. s л <\ displaystyle <\ mathfrak Две матрицы X и Y называются ортогональными по следу, если Для матрицы A размера m × n с комплексными (или действительными) элементами и H, являющимся сопряженным транспонированием, имеем Если K является следовым классом, то для любого ортонормированного базиса след определяется выражением ( φ п ) п <\ Displaystyle (\ varphi _ <п>) _ <п>> и конечна и не зависит от ортонормированного базиса. Операция тензорного сжатия обобщает след на произвольные тензоры. К следу можно также подойти безкоординатным образом, т. Е. Без обращения к выбору базиса, следующим образом: пространство линейных операторов в конечномерном векторном пространстве V (определенном над полем F ) изоморфно пространству пространство V ⊗ V ∗ линейным отображением Существует также каноническая билинейная функция t : V × V ∗ → F, которая состоит в применении элемента w ∗ из V ∗ к элементу v из V, чтобы получить элемент из F : можно интерпретировать композиционную карту ( V ⊗ V * ) × ( V ⊗ V * ) → ( V ⊗ V * ) <\ displaystyle (V \ otimes V ^ <*>) \ times (V \ otimes V ^ <*>) \ to (V \ otimes V ^ <*>)> происходит от спаривания V ∗ × V → F на средних членах. Отслеживание следа продукта происходит в результате спаривания на внешних терминах, при взятии продукта в обратном порядке и последующем взятии следа просто выбирается, какое спаривание применяется первым. С другой стороны, взятие следа A и следа B соответствует применению спаривания к левым и правым членам (а не к внутреннему и внешнему) и, таким образом, отличается. В координатах это соответствует индексам: умножение дается на что то же самое, в то время как Если t определено, как указано выше, Далее, можно дуализировать эту карту, получив карту Затем можно составить их, F,> ><\to >>K\to 0> Билинейные формы [ править ]
Внутренний продукт [ править ]
Обобщения [ править ]
Определение без координат [ править ]
Двойной [ править ]
Обобщения [ править ]
СОДЕРЖАНИЕ
Определение
Пример
Характеристики
Основные свойства
След продукта
Циклическое свойство
След матричного произведения
След продукта Кронекера
Полная характеристика следа
Инвариантность подобия
След произведения симметричной и кососимметричной матрицы
Отношение к собственным значениям
След единичной матрицы
След идемпотентной матрицы
След нильпотентной матрицы
Трассировка равна сумме собственных значений
След коммутатора
След эрмитовой матрицы
След матрицы перестановок
След матрицы проекции
Экспоненциальный след
След линейного оператора
Отношения собственных значений
Производные
Приложения
Алгебра Ли
> <\ to>> K \ to 0> Билинейные формы
Внутренний продукт
Обобщения
Безкоординатное определение
Двойной
Обобщения