скорость звука в воде выше чем в воздухе
Разгадана тайна быстрого звука в воде
Эксперименты итальянских физиков позволили наконец-то дать окончательное объяснение явлению быстрого звука в воде. Из двух существующих сегодня теорий — вискоэластичной и двухкомпонентной — эти эксперименты подтвердили первую и опровергли вторую.
В обычных условиях скорость звука в воде составляет примерно 1,5 километра в секунду и не зависит от частоты звуковой волны. Однако уже давно известно, что ультразвуковые колебания с частотой несколько терагерц (1 терагерц = 10 12 Гц) распространяются в воде со скоростью примерно вдвое большей. Это явление было открыто экспериментально 20 лет назад, намеки на него появлялись и при численном моделировании динамики воды на атомарном уровне, но несмотря на всё это общепринятого его объяснения до сих пор не было. Только сейчас, благодаря экспериментам итальянских физиков, опубликованных в статье S. C. Santucci et al., Physical Review Letters, 97, 225701 (27 November 2006), в природе этого явления расставлены все точки над «i» (статья доступна также на сайте авторов, PDF, 274 Кб).
Сразу стоит подчеркнуть, что опыты со столь высокочастотным ультразвуком ставить очень непросто. Акустические излучатели в этом диапазоне пока не придуманы, и потому физикам приходится определять скорость такого ультразвука косвенными методами. Для этого воду облучают потоком нейтронов или рентгеновских лучей, которые, сталкиваясь с молекулами воды, порождают в микроскопическом объемчике быстрые колебания и передают им часть своей энергии и импульса. Из соотношения этих двух величин и выводится скорость распространения звуковых колебаний.
На сегодня существует две основных теории, претендующих на объяснение этого явления. В соответствии с первой, для звука всё более высокой частоты вода становится всё более упругой и всё менее подвижной средой (такие среды называются вискоэластиками). В результате колебания с такой высокой частотой распространяются скорее через упругую, почти твердую среду, а в твердом теле скорость звука выше, чем в жидкости (скорость звука во льду, например, как раз и составляет примерно 3 км/сек).
Вторая теория основана на том факте, что вода состоит из переплетенной сети ионов двух типов: очень легких ионов водорода и тяжелых ионов кислорода. Вычисления показывают, что часто в таких двухкомпонентных средах с сильно различающимися массами существует специальный тип быстрых звуковых волн, которые распространяются исключительно через сеть легких атомов. Эта теория уже хорошо себя зарекомендовала для описания быстрого звука в двухкомпонентных газах и металлических сплавах, и потому кажется естественным, что она будет работать и для воды.
Обе эти модели, разумеется, согласуются с описанными выше экспериментами, однако они совершенно по-разному описывают переход от нормального звука к быстрому, который должен происходить при меньших частотах, в гигагерцевом диапазоне. Поэтому для ответа на вопрос, какая из двух моделей верна, требуется измерить зависимость скорости звука от частоты в этой промежуточной области. Дополнительная сложность такого эксперимента состоит в том, что наиболее четко переход от нормального к быстрому звуку проявляется в очень холодной и даже переохлажденной воде (то есть ниже нуля градусов Цельсия). Эксперименты с переохлажденной водой требуют сноровки, поскольку при малейшем возмущении она быстро кристаллизуется.
Именно этот опыт и поставили итальянские физики. Изучая рассеяние оптических и ультрафиолетовых фотонов, они смогли просканировать частотный диапазон звуковых колебаний от 1 до 100 ГГц и впервые получили точные данные о скорости звуковых колебаний в этом диапазоне. Эксперимент абсолютно четко показал, что при повышении частоты (или при понижении температуры) скорость звука действительно постепенно отходит от «нормальной» зависимости и начинает расти (в существовании такого плавного перехода, кстати, мнения тоже разделялись).
Кроме того, авторы статьи сравнили свои данные с предсказаниями обеих моделей и доказали, что эксперимент подтверждает вискоэластичную модель и противоречит выводам двухкомпонентной модели. Таким образом, можно считать, что в многолетнем споре приверженцев двух моделей поставлена точка. В целом же, эта работа лишний раз подчеркивает поразительное разнообразие структурных и динамических свойств воды (для дальнейшего ознакомления см. популярную статью: Ю. И. Головин. Вода и лед — знаем ли мы о них достаточно? // СОЖ, 2000, № 9, с. 66–72).
Звук (звуковые волны). Скорость звука.
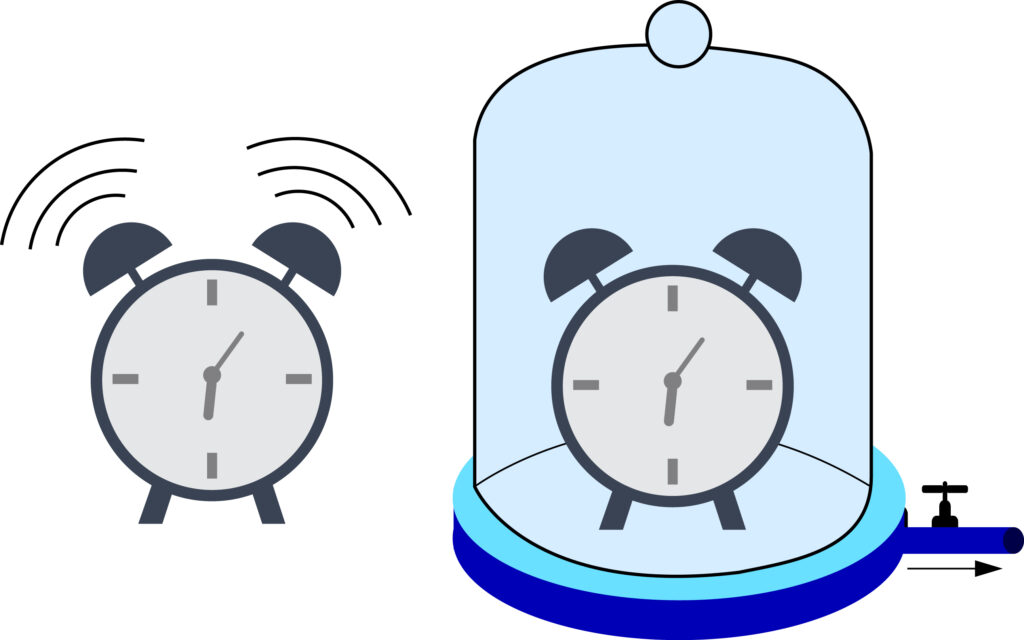
Для распространения звука необходима упругая среда. В вакууме звуковые волны распространяться не могут, так как там нечему колебаться. В этом можно убедиться на простом опыте. Если поместить под стеклянный колокол электрический звонок, то по мере выкачивания из-под колокола воздуха звук от звонка будет становиться все слабее и слабее, пока не прекратится совсем.
Известно, что во время грозы мы видим вспышку молнии и лишь через некоторое время слышим раскаты грома. Это запаздывание возникает из-за того, что скорость звука в воздухе значительно меньше скорости света, идущего от молнии.
Скорость звука в воздухе впервые была измерена в 1636 г. французским ученым М. Мерсенном. При температуре 20 °С она равна 343 м/с, т. е. 1235 км/ч. Заметим, что именно до такого значения уменьшается на расстоянии 800 м скорость пули, вылетевшей из автомата Калашникова. Начальная скорость пули 825 м/с, что значительно превышает скорость звука в воздухе. Поэтому человек, услышавший звук выстрела или свист пули, может не беспокоиться: эта пуля его уже миновала. Пуля обгоняет звук выстрела и достигает своей жертвы до того, как приходит этот звук.
Скорость звука в газах зависит от температуры среды: с увеличением температуры воздуха она возрастает, а с уменьшением — убывает. При 0 °С скорость звука в воздухе составляет 332 м/с.
В разных газах звук распространяется с разной скоростью. Чем больше масса молекул газа, тем меньше скорость звука в нем. Так, при температуре 0 °С скорость звука в водороде составляет 1284 м/с, в гелии — 965 м/с, а в кислороде — 316 м/с.
Скорость звука в твердых телах больше, чем в жидкостях и газах. Если приложить ухо к рельсу, то после удара по другому концу рельса слышно два звука. Один из них достигает уха по рельсу, другой — по воздуху.
Хорошей проводимостью звука обладает земля. Поэтому в старые времена при осаде в крепостных стенах помещали «слухачей», которые по звуку, передаваемому землей, могли определить, ведет ли враг подкоп к стенам или нет. Прикладывая ухо к земле, также следили за приближением вражеской конницы.
Твердые тела хорошо проводят звук. Благодаря этому люди, потерявшие слух, иной раз способны танцевать под музыку, которая доходит до слуховых нервов не через воздух и наружное ухо, а через пол и кости.
Скорость звука можно определить, зная длину волны и частоту (или период) колебаний:
Звуковые волны
Звуковые волны или звук – это колебания частиц, распространяемые волнообразно в какой-либо среде – газообразной, жидкой или твёрдой, – которые воспринимаются органами слуха животных.
Когда мы изучаем свет, то убеждаемся не только в том, что он существует вне нас, но сверх того еще и в том, что нам необходимо иметь глаза для восприятия света, иначе мы и не подозревали бы о нем. Всё вокруг нас погружается в темноту, когда мы закрываем глаза. Точно так же для нас не существовало бы мира звуков, если бы у нас не было органа слуха, который воспринимает их.
Итак, мы называем звуком то, что мы чувствуем нашим слуховым аппаратом. Но явления внешнего мира для нас имеют характер звуковых только с того момента, когда они дошли до наших ушей. Закрыв уши пальцами, мы не услышим разговора, хотя он и продолжается около нас.
Из этого следует, что как бы ни были грандиозны звуковые явления, происходящие на Солнце и Луне, они не могут произвести такого шума, который мог бы быть услышан у нас на Земле, потому что за пределами нашей атмосферы, между Землей и небесными телами, нет обычной материи.
Источники звуковых волн
Мы говорим, что звук есть волнообразные движения или колебания. Каждый, кто видел или чувствовал то, что происходит, когда рождается звук, тотчас согласится с этим. Так, например, если крепко натянуть нить и потом быстро ударить по ней, то можно видеть, как она заколеблется. И услышать при этом небольшой музыкальный звук. То же самое будет наблюдаться в звучащей фортепианной струне или в колоколе. И мы можем ощущать эти колебания, если дотронемся до них.
Мы также знаем, что при ударе по стеклу оно издает звук, который прекращается, если прикосновением пальца прекратить его колебания. Все эти явления служат доказательством того, что известные колебания производят звук. Каждый раз, когда колеблется колокольчик, стакан или струна, воздух получает от них легкие удары. В нем образуется ряд волн, доходящих до нашего уха, вот почему мы и слышим звук.
Нетрудно доказать, что воздух проводит звуковые волны. Для этой цели производят следующий опыт: под стеклянный колпак воздушного насоса помещают электрический звонок, заставляют его непрерывно звенеть. Затем начинают насосом выкачивать воздух.
Когда уменьшается количество воздуха под колпаком, мы видим звонок так же хорошо, как и раньше, потому что свет распространяется, когда воздуха нет. Но звук делается все тише и наконец совершению прекращается. Колебания звонка продолжают совершаться, но так как вокруг него больше нет воздуха, то он не может производить те волны. которые мы называем звуковыми. Если же воздух начинает снова входить под колпак, то звук восстанавливается. Этот простой опыт показывает нам не только то, что воздух служит проводником звука, но и то, что сила звука в значительной степени зависит от состояния воздуха.
Когда у нас появляется возможность сравнить скорость света со скоростью звука, то мы находим между ними огромное различие. Но видим огонь и дым при стрельбе из отдаленной пушки на несколько секунд раньше звука от ее выстрела. Свет распространяется так быстро, что даже значительное расстояние, на котором находится от нас действующее орудие, он проходит в какую-нибудь тысячную долю секунды; тогда как звук распространяется гораздо медленнее, и скорость его распространения при таком опыте очень легко вычислить.
Распространение звуковых волн
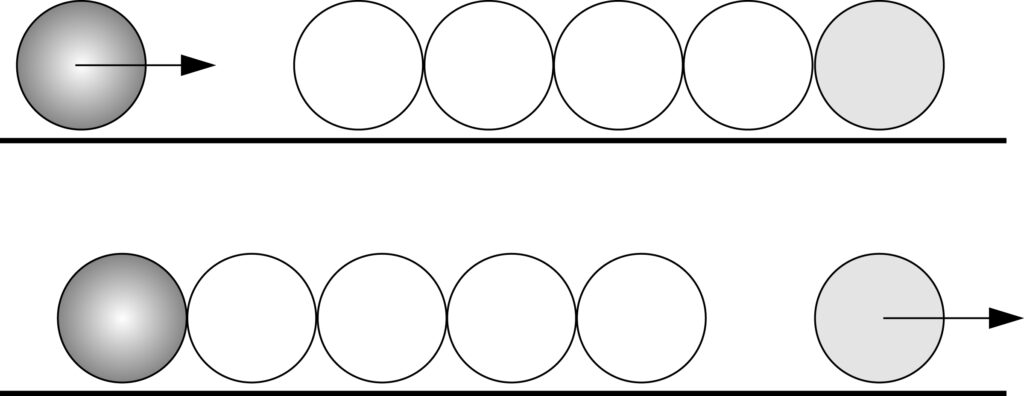
Возьмем несколько бильярдных шаров и положим их прямой линией на бильярдном столе так, чтобы они касались друг друга. Затем возьмем еще шар и покатим его так, чтобы он ударил в шар, лежащий на конце ряда. Тогда каждый из шаров в ряду будет попеременно сжиматься и производить давление на следующий за ним, в результате чего шар, находящийся на другом конце ряда, отскочит от него.
Каждый шар ряда здесь попеременно сжимается и расширяется. То же самое случается и в воздухе, когда звук проходит через него. Мы можем представить себе, что волну принуждают двигаться частицы воздуха, ударяющие одна о другую при своих движениях взад и вперед, точно так, как эти бильярдные шары.
Скорость звука
Скорость света одинакова при всех условиях, насколько это можно было изучить. А скорость звука изменяется в значительной степени с изменением условий, при которых он распространяется в воздухе. Большое счастье для музыкального искусства заключается в том, что скорость звука изменяется только в незначительной степени с изменением высоты его или силы.
Было бы очень затруднительно слушать издали музыку, если бы звуки различных инструментов оркестра доходили до нашего слуха в разное время, в то время как композитор имел в виду, что они будут слышаться одновременно. Или, если бы мотив, разыгрываемый одной частью оркестра, доходил до нашего слуха раньше того, что играет другая часть оркестра, или позже.
1. Скорость звука в воздухе
Обычная скорость звука в воздухе считается около 331 метра (То есть около трети километра) в секунду. Когда температура воздуха поднимается, он становится более упругим и тогда прохождение звука через него совершается быстрее.
Скорость звука увеличивается с повышением температуры воздуха, если плотность его остается той же самой.
Если мы примем во внимание зависимость скорости звука от упругости проводящей его среды, то нам будет понятно, почему звук проходит значительно быстрее в жидкостях, чем в газах, и еще быстрее в твердых телах.
2. Скорость звуковых волн в твёрдых телах
Звуковые волны распространяются в твёрдых телах быстрее, чем в воздухе. Железо, когда оно в твердом состоянии, обладает большею упругостью, чем воздух, и звук проходит в нем почти в семнадцать раз быстрее, чем в воздухе
Нельзя смешивать скорость распространения звука в воздухе или в какой-либо другой среде с высотой тона. Она у музыкального звука зависит от числа колебаний в секунду, и чем их больше, тем выше тон.
Звук, как мы сказали, проходя через железо, достигает нашего уха в семнадцать раз быстрее, чем когда он проходит через воздух; высота же его тона остается той же самой в обоих случаях, потому что число колебаний в секунду остается одно и то же, хотя звук через железо проходит значительно быстрее.
3. Скорость звука в разных средах
Сила звука
Когда мы начнем исследовать силу звука на разных расстояниях, то найдем, что первый закон, относительно его, тот же, что и для света. И насколько нам известно, этот закон верен не только относительно волнообразных движений, но и такого явления, как тяготение.
На точном научном языке закон о силе звука излагается так:
Сила звука изменяется обратно пропорционально квадрату расстояния от его источника
Таким образом можно коротко и ясно выразить, например, ту мысль, что если мы удаляемся от источника звука на расстояние, которое в три раза больше прежнего, то сила звука уменьшится при этом не в три, а в девять раз: девять есть квадрат трех. Квадратом числа называется число, полученное от перемножения его на самого себя.
Когда этот закон применяется к силе света или тяготения, то нам не приходится считаться с какими-либо условиями, которые могут повлиять на них. Но если речь идёт о звуке, то дело обстоит несколько иначе. На звук влияет плотность той среды, в которой он проходит; в морозную ночь воздух очень плотен, почему нам и дышится тогда легче, звук же будет в это время слышен сильнее. С другой стороны, звук ружейного выстрела высоко в горах ослабляется, потому что воздух там редок. Это явление напоминает нам опыт со звонком под колпаком воздушного насоса.
Отражение звука
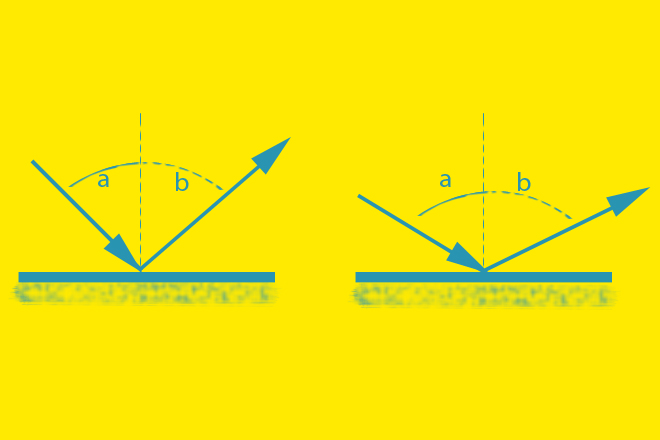
Когда мы наблюдаем, как волны моря или озера ударяют в крутой берег, мы видим, что они отражаются от него и отскакивают назад. Если поверхность берега ровная и вертикальная, то мы видим, что волны отражаются от нее точно так же, как мяч от стены. Если звук есть действительно волнообразное движение, то мы всегда можем ожидать, что и он будет так же отражаться, как водяные волны, и нам часто приходится убеждаться в этом.
Всякие движущиеся волны могут отражаться от преград на их пути; это совершается как при свете, так и при морских волнах. Есть законы отражения, которые одинаково приложимы к этим различным явлениям.
Природа грома
Мы все хорошо знаем, что на открытом воздухе звук кажется нам не таким, как в закрытом помещении. И наш голос в разных местах звучит различно. Все эти явления зависят от особенностей отражения звука в разных местах.
Самым лучшим способом для доказательства отражения звука может служить эхо. Мы можем довольно простым способом определить скорость звука, стоит только нам произвести звук на некотором расстоянии от отражающей его поверхности и заметить, как быстро мы услышим эхо.
Лучшим примером отражения звука, производящего эхо, являются раскаты грома, случающиеся во время грозы:
Волны Рэлея
Если мы наполним резиновый шар или выпуклый диск углекислым газом, то заметим, что он действует на звук точно так, как зажигательное стекло на световые лучи. Звуковые волны отклоняются газом, находящимся в шаре, так что они все собираются в одном пункте, находящемся по другую сторону шара точно так, как лучи солнца могут быть собраны на кусок бумаги в одну точку зажигательным стеклом.
Это видно из хорошо известного опыта, произведенного замечательным английским ученым, лордом Рэлеем. Опыт этот заключается в том, что нас ставят против часов на таком расстоянии, чтобы не слышать их тиканья. Если после этого гуттаперчевый шар, наполненный углекислым газом, будет помещен между нами и часами, то, находясь на том же самом расстоянии, мы услышим часы. Это происходит вследствие того, что углекислый газ преломляет звуковые волны и фокусирует их в одной точке.
Скорость звука
| Азот | 334 |
| Аммиак | 415 |
| Ацетилен | 327 |
| Водород | 1284 |
| Воздух | 331 |
| Гелий | 965 |
| Кислород | 316 |
| Метан | 430 |
| Угарный газ | 338 |
| Углекислый газ | 259 |
| Хлор | 206 |
Скорость звука — скорость распространения упругих волн в среде — как продольных в газах, жидкостях и твердых телах, так и поперечных (сдвиговых) в твердой среде. Определяется упругостью и плотностью среды. Скорость звука в газах не является величиной постоянной и зависит от температуры данного вещества, в монокристаллах зависит от направления распространения волны и при заданных внешних условиях обычно не зависит от частоты волны и её амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом.
Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, поэтому при сжижении газа скорость звука возрастает.
Содержание
Расчёт скорости в жидкости и газе
Скорость звука в однородной жидкости (или газе) вычисляется по формуле:
где 
— адиабатическая сжимаемость среды; 
— плотность.
Для газов эта формула выглядит так:
где 
— показатель адиабаты: 5/3 для одноатомных газов, 7/5 для двухатомных (и для воздуха), 4/3 для многоатомных; 
— постоянная Больцмана; 
— универсальная газовая постоянная; 
— абсолютная температура в кельвинах; 
— температура в градусах Цельсия; 
— молекулярная масса; 
— молярная масса. По порядку величины скорость звука в газах близка к средней скорости теплового движения молекул и в приближении постоянства показателя адиабаты пропорциональна квадратному корню из абсолютной температуры.
Данные выражения являются приближенными, поскольку основываются на уравнениях, описывающих поведение идеального газа. При больших давлениях и температурах необходимо вносить соответствующие поправки.
Для расчета сжимаемости многокомпонентной смеси, состоящей из невзаимодействующих друг с другом жидкостей и/или газов, применяется уравнение Вуда. Это же уравнение применимо и для оценки скорости звука в нейтральных взвесях.
Для растворов и других сложных физико-химических систем (например, природный газ, нефть) данные выражения могут давать очень большую погрешность.
Твёрдые тела
В однородных твёрдых телах могут существовать два типа объемных волн, отличающихся друг от друга поляризацией колебаний относительно направления распространения волны: продольная (P-волна) и поперечная (S-волна). Скорость распространения первой 
всегда выше, чем скорость второй 
:
где 
— модуль всестороннего сжатия; 
— модуль сдвига; 
— модуль Юнга; 
— коэффициент Пуассона. Как и для случая с жидкой или газообразной средой, при расчетах должны использоваться адиабатические модули упругости.
В многофазных средах из-за явлений неупругого поглощения энергии скорость звука, вообще говоря, зависит от частоты колебаний (то есть наблюдается дисперсия скорости). Например, оценка скорости упругих волн в двухфазной пористой среде может быть выполнена с применением уравнений теории Био-Николаевского. При достаточно высоких частотах (выше частоты Био) в такой среде возникают не только продольные и поперечные волны, но также и продольная волна II-рода. При частоте колебаний ниже частоты Био, скорость упругих волн может быть приблизительно оценена с использованием гораздо более простых уравнений Гассмана.
При наличии границ раздела, упругая энергия может передаваться посредством поверхностных волн различных типов, скорость которых отличается от скорости продольных и поперечных волн. Энергия этих колебаний может во много раз превосходить энергию объемных волн.
Скорость звука в воде
В чистой воде скорость звука составляет 1500 м/с (см. опыт Колладона—Штурма). Прикладное значение имеет также скорость звука в солёной воде океана. Скорость звука увеличивается в более солёной и более тёплой воде. При большем давлении скорость также возрастает, то есть чем глубже, тем скорость звука больше. Разработано несколько теорий распространения звука в воде.
Например, теория Вильсона 1960 года для нулевой глубины даёт следующее значение скорости звука:
,
Иногда также пользуются упрощённой формулой Лероя:
,