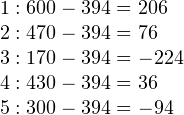ско в метрологии что это

Как найти среднеквадратическое отклонение

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом 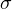(греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее 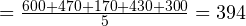мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

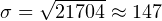
Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

При этом стандартное отклонение по выборке равно 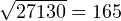мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

.

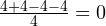
Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

.

.

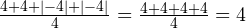
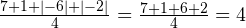
Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

.

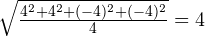
Для второго примера получится:

.

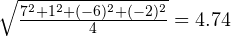
Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Источник

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Источник

Статистические данные

Слово статистика образовано от латинского status, которое обозначает состояние. От этого корня произошли слова stato (государство), statistica (сумма знаний о государстве). Математическая статистика — наука, которая изучает методы сбора и обработки информации, представленной в численном виде. Эта информация появляется как результат экспериментов. Во многом математическая статистика опирается на теорию вероятностей, которая позволяет оценить точность и надёжность заключений, сделанных на основании изучения ограниченных статистических данных.

Метод не исследует сущность процессов, а формулирует и описывает их количественную сторону. Термином генеральная совокупность обозначается общность всех объектов, относительно которых необходимо сделать выводы при изучении научной проблемы. Выборочная совокупность или выборка — множество объектов, отобранных из генеральной совокупности для исследования. Основные цели математической статистики:

Главный метод математической статистики — выборочный метод, состоящий в исследовании представительной выборочной совокупности для получения достоверной характеристики генеральной. Отбор объектов в выборку производится случайно, а исследуемое свойство должно обладать статистической устойчивостью, то есть иметь высокую частоту повторений при многократных испытаниях.

Выборочный метод сокращает время и трудоёмкость исследований, так как изучение всей совокупности оказывается более тяжёлым или невозможным. Математическая статистика выявляет закономерности массовых явлений и предсказывает появление внешних влияний.

Размах вариации

Вариация — это различия значений признака у единиц исследуемой совокупности. Она образуется из-за того, что индивидуальные значения формируются при различных условиях. Выборка должна быть представительной, чтобы по результатам её исследований можно было сделать правильные выводы о характеристиках всей совокупности.

Количественная репрезентативность достигается при использовании достаточного числа наблюдений в выборке, которое может обеспечить получение достоверных результатов. Качественная репрезентативность заключается в одинаковой структуре выборочной и генеральной совокупностей по признакам, имеющим влияние на получение конечного результата. К абсолютным показателям вариации относятся:

Размах вариации показывает абсолютную разницу между максимумом и минимумом значений признака:

R = x max — x min, где x — значения признака.

Основным недостатком показателя R можно назвать то обстоятельство, что колебания значений признака могут вызываться случайными причинами и искажать характерный для исследуемой совокупности размах.

Показатели отклонения

Существуют показатели вариации, учитывающие все значения величин, а не только наибольшие или наименьшие. Одним из них можно назвать среднее линейное отклонение — показатель, характеризующий меру разброса значений. Сначала требуется определить точку отсчёта разброса. Как правило, ею становится среднее арифметическое значение, входящее в исследование величин. Потом необходимо измерить, отклонение от среднего для каждого значения. Все отклонения вычисляются по модулю и определяется среднее значение уже среди них. Формула для расчёта отклонения:

a = Σ n i=1 (x — x̅) / n, где:

Коэффициент вариации

Квадратичное отклонение — это абсолютная оценка меры разброса. Для того чтобы сравнить величину разброса с самими значениями величины, необходимо применить относительный показатель — коэффициент вариации:

V = σ / x̅, где σ — стандартное отклонение из выборки, x̅ — среднее арифметическое.

Коэффициент вариации измеряется в процентах. Показатель полезен для сравнивания однородности разных процессов.

Математическое ожидание — среднее значение случайной величины. Для дискретной выборки оно определяется по формуле:

M (X)= Σ n i=1 xi ⋅ pi, где xi — случайные значения, pi — их вероятность.

Дисперсией называется среднее значение квадрата отклонения случайной величины от её математического ожидания:

D (X) = M (X 2 ) — (M (X)) 2

Для дискретной случайной величины формула приобретает вид:

Среднеквадратическое отклонение или стандартный разброс — это корень квадратный из дисперсии, формула которого имеет вид:

Дисперсия и стандартный разброс — взаимозависимые характеристики. Стандартная ошибка среднего — величина, которая характеризует квадратическое отклонение выборочного среднего, рассчитанного по выборке размера из генеральной совокупности. Величина ошибки SDx̅ зависит от дисперсии генеральной совокупности и объёма выборки и рассчитывается по формуле:

SDx̅ = σ / √ n, где σ — величина стандартного разброса генеральной совокупности, а n — объём выборки.

Статистическая закономерность — это количественная форма проявления причинной связи. Она возникает как результат воздействия большого числа причин, действующих либо постоянно, либо только временами. Существует ряд статистических критериев, которые позволяют сравнивать экспериментально полученное распределение с нормальным, полученным в теории. Погрешность измерения — отклонение измеренного значения величины от действительного, являющиеся характеристикой точности измерения. Вместе с полученным результатом должна указываться погрешность измерений.

Пример расчёта

Пример расчёта по формулам для среднеквадратичного отклонения и дисперсии при решении следующей задачи по теории вероятностей: для выполнения ремонтных работ рабочему необходима краска определённого цвета. В городе имеется четыре строительных магазина, в каждом из которых эта краска может находиться в продаже с вероятностью 0,41. Записать закон распределения количества посещаемых магазинов. Рассчитать дисперсию и среднеквадратичное отклонение случайной величины. Обход заканчивается после того, как необходимая краска будет куплена или после посещения всех четырёх магазинов.

x = 1 — краска куплена в первом магазине.

x = 2 — краски не нашлось в первом магазине, но она была во втором.

p (2) = (1 — 0,41) · 0,41 = 0,59 · 0,41 = 0,242.

x = 3 — краски не нашлось в двух первых магазинах, но она была в третьем.

p (3) = (1 — 0,41) 2 · 0,41 = 0,59 2 · 0,41 = 0,143.

x = 4 — краски не было в первых трёх магазинах, рабочий зашёл в четвёртый магазин, купил краску или просто закончил обход.

p (4) = 0,59 3 · 0,41 + 0,59 4 = 0,205.

Закон распределения:

Математическое ожидание: M (X) = 1 · 0,41 + 2 · 0.242 + 3 · 0,143 + 4 · 0,205 = 2,143.

Дисперсия: D (X) = Σ n i=1 xi 2 ⋅ pi — M (X) 2 = 1 2 · 0,41 + 2 2 · 0,242 + 3 2 · 0,143 + 4 2 · 0,205 — 2,143 2 = 1,353.

Стандартное отклонение: σ(X) = √ D (X) = √1,353 = 1,163.

Ответ: Дисперсия 1,353; квадратическое отклонение 1,163.

Для вычисления среднеквадратичного отклонения в онлайн-калькуляторе достаточно внести в таблицу значения случайной величины xi и их количество.

Среднеквадратичное отклонение применяется для определения погрешности при проведении последовательных измерений. Эта характеристика играет важную роль для сравнения изучаемого процесса с теоретически предсказанным. Если СКО велико, то полученные результаты или метод их получения нужно проверить.

Источник

Ско в метрологии что это

Всероссийский научно-исследовательский институт
оптико-физических измерений

ПОИСК И НАВИГАЦИЯ

МЫ НА YOUTUBE

Погрешности измерений

Погрешность результата измерения (англ. error of a measurement) – отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Примечания:

Инструментальная погрешность измерения (англ. instrumental error) – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.

Погрешность метода измерений (англ. error of method) – составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.
Примечания:

Погрешность (измерения) из-за изменений условий измерения – составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Примечание. Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.

Субъективная погрешность измерения – составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора.
Примечания:

Неисключенная систематическая погрешность – составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
Примечания:

Случайная погрешность измерения (англ. random error) – составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.

Абсолютная погрешность измерения (англ. absolute error of a measurement) – погрешность измерения, выраженная в единицах измеряемой величины.

Абсолютное значение погрешности (англ. absolute value of an error) – значение погрешности без учета ее знака (модуль погрешности).
Примечание. Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности.

Относительная погрешность измерения (англ. relative error) – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
Примечание. Относительную погрешность в долях или процентах находят из отношений:

Рассеяние результатов в ряду измерений (англ. dispersion) – несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.
Примечания:

Размах результатов измерений (англ. ) – оценка R_n рассеяния результатов единичных измерений физической n величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле:

Среднее квадратическое отклонение результатов единичных измерений в ряду измерений (англ. experimental (sample) standard deviation) – характеристика S рассеяния результатов измерений в ряду равноточных измерений одной и той же физической величины, вычисляемая по формуле:

Среднее квадратическое отклонение среднего арифметического значения результатов измерений (англ. experimental (sample) standard deviation) – характеристика S_x рассеяния среднего арифметического значения результатов равноточных измерений одной и той же величины, вычисляемая по формуле:

Доверительные границы погрешности результата измерений – наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

Поправка (англ. correction) – значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.
Примечание. Знак поправки противоположен знаку погрешности. Поправку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора.

Поправочный множитель (англ. correction factor) – числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.
Примечание. Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению величины.

Точность результата измерений (англ. accuracy of measurement) – одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Примечание. Считают, что чем меньше погрешность измерения, тем больше его точность.

Неопределенность измерений (англ. uncertainty of measurement) – параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.

Погрешность метода поверки – погрешность применяемого метода передачи размера единицы при поверке.

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешность воспроизведения единицы физической величины – погрешность результата измерений, выполняемых при воспроизведении единицы физической величины.
Примечание. Погрешность воспроизведения единицы при помощи государственных эталонов обычно указывают в виде ее составляющих: неисключенной систематической погрешности; случайной погрешности; нестабильности за год.

Погрешность передачи размера единицы физической величины – погрешность результата измерений, выполняемых при передаче размера единицы.
Примечание. В погрешность передачи размера единицы входят как неисключенные систематические, так и случайные погрешности метода и средств измерений.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения.

Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения.

Промах – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Примечание. Иногда вместо термина промах применяют термин грубая погрешность измерений.

Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.

Погрешность результата однократного измерения – погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях (измерений).
Пример. При однократном измерении микрометром какого-либо размера детали получено значение величины, равное 12,55 мм. При этом еще до измерения известно, что погрешность микрометра в данном диапазоне составляет +/- 0,01 мм, и погрешность метода (непосредственной оценки) в данном случае принята равной нулю. Следовательно, погрешность полученного результата будет равна +/- 0,01 мм в данных условиях измерений.

Суммарное среднее квадратическое отклонение среднего арифметического значения результатов измерений – характеристика S_∑ рассеяния среднего арифметического результатов измерений, обусловленная влиянием случайных и неисключенных систематических погрешностей и вычисляемая по формуле:

Источник

• ← сирень около дома приметы
• прочистка труб на даче →