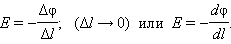работа в потенциальном поле
Работа в потенциальном поле
Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле
Электростатическое поле обладает важным свойством:
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
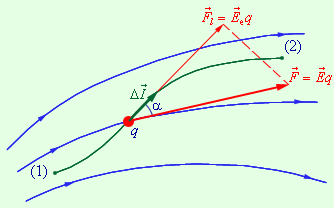
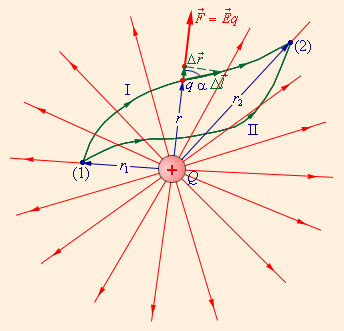
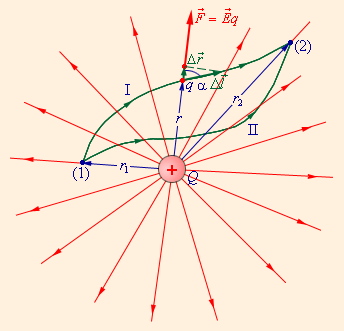
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда и две различные траектории перемещения пробного заряда из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение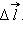 
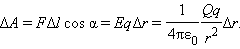Работа Δ кулоновских сил на этом перемещении равна
 |
Таким образом, работа на малом перемещении зависит только от расстояния между зарядами и его изменения Δ. Если это выражение проинтегрировать на интервале от = 1 до = 2, то можно получить
 |
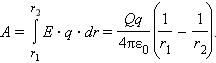Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Если электростатическое поле создается совокупностью точечных зарядов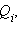 
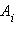
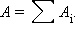
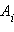
то при перемещении пробного заряда работа результирующего поля в соответствии с принципом суперпозиции будет складываться из работ 
кулоновских полей точечных зарядов: 
Так как каждый член суммы 
не зависит от формы траектории, то и полная работа результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электростатическое полем при перемещении точечного заряда из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
|
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
|
Потенциал φ является энергетической характеристикой электростатического поля.
Работа 12 по перемещению электрического заряда из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
| 12 = p1 – p2 = φ1 – φ2 = (φ1 – φ2). |
В Международной системе единиц (СИ) единицей потенциала является вольт (В).
Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
|
Потенциал φ∞ поля точечного заряда на расстоянии от него относительно бесконечно удаленной точки вычисляется следующим образом:
 |
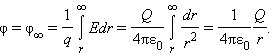Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.
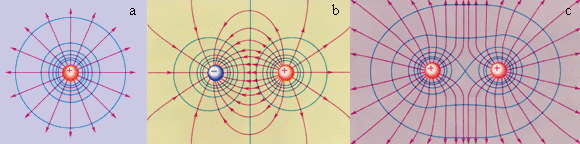
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Если пробный заряд совершил малое перемещение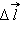 
вдоль силовой линии из точки (1) в точку (2), то можно записать:
| Δ12 = Δ = (φ1 – φ2) = – Δφ, |
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует
 |
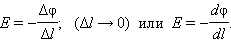Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь – координата, отсчитываемая вдоль силовой линии.
Работа в электрическом поле. Потенциал
Работа сил электростатического поля. Понятие потенциала
Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.
При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.
У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.
Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:
Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны. Если же мы изменим направление на противоположное, то и работа также поменяет знак. А если траектории будут соединены, т.е. заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.
Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов. Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле. Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.
Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.
Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки). На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет. Важна лишь разность ее значений в начальной и конечной точке пространства.
Если мы поместим заряд q в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.
Понятие потенциала электрического поля
Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.
Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.
Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:
Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.
φ = φ ∞ = 1 q ∫ r ∞ E d r = Q 4 π ε 0 ∫ r ∞ d r r 2 = 1 4 π ε 0 Q r
Изображение электрических полей с помощью эквипотенциальных поверхностей
Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.
Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.
Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.
Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.
Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.
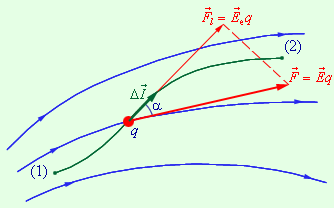
В случае малого перемещения пробного заряда q вдоль силовой линии из начальной точки 1 в конечную точку 2 мы можем записать такую формулу:
Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой l обозначена координата, которую следует отсчитывать вдоль силовой линии.
Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:
Работа в потенциальном поле
Фролов Александр Владимирович
Научный Эксперт Русского Физического Общества
Извлечение мощности в точке меняющегося потенциала
как результат изменения величины потенциала в процессе движения от тела M на бесконечное расстояние.
Электрическое напряжение U известно как разность потенциалов между двумя точками, расположенными на некотором расстоянии друг от друга в пространстве,
Работа и мощность являются результатами этого движения, поскольку градиент потенциала означает некоторое изменение величины энергии (преобразование энергии).
Для различия с обычным градиентом, используем обозначение « grad j ( t )». Хрональному градиенту соответствует определенная напряженность:
Напряженность хронального поля в точке C создается в том случае, если потенциал является функцией времени. Изменение энергии (преобразование энергии) создает работу, поэтому хрональное поле в одной точке пространства может быть использовано как источник мощности и движущая сила. Движение, в данном случае, происходит во времени.
Работа зависит от хронального напряжения и определяется как производная по времени:
A = Dj / D t = j ‘(t) F.5
Отметим, что это работа по перемещению материальной заряженной частицы вдоль оси времени. Технические системы по извлечению мощности, в данном случае, должны включать «элемент памяти» для того, чтобы делать сравнение между прошлым значением потенциала j A ( t ) и будущим значением j B ( t ). Примером этого устройства является электрический конденсатор, используемый в схеме на Рис.1.
Отметим, что величина потенциала может быть переменной или пульсирующей. Частота и амплитуда изменений задают мощность на выходе. Кроме того, существенным фактором для мощности в нагрузке является число свободных электронов в проводе, ограничивающих возможность увеличения силы тока в нагрузке.
По аналогии с обычной электродвижущей силой ЭДС, которая производится любым источником разности потенциалов в пространстве, введем понятие хронодвижущей силы ХДС. Поле данной силы расположено не в пространстве, а во времени. Еще раз отметим, что результатом действия ХДС на частицы материи является перемещение во времени.
Постоянная ХДС в данной точке пространства есть результат однонаправленного изменения величины потенциала по времени. Природа массы демонстрирует однонаправленное движение из прошлого в будущее. Согласно предлагаемой здесь теории, это движение есть результат некоторого постоянного изменения величины потенциала. Это изменение является глобальным, поскольку эффект (так называемый естественный поток времени) обнаруживается во всех точках нашего пространства-времени.
Однонаправленное изменение величины потенциала, например, электрического, может быть использовано в экспериментах для того, чтобы производить локальные изменения скорости хода времени, детектируемых по изменению скорости процессов существования материи.
Тесловская концепция беспроводной передачи мощности
В своей статье [4] Тесла описывает концепцию передачи мощности за счет источника высокочастотных колебаний электрического поля. Величина потенциала, который использовал Тесла была также очень высокая. Есть принципиальная разница в схемах Тесла и привычного нам передатчика волн Герца.
Итак, в схеме, рассматриваемой на Рис.2, нет направленного радиолуча. При резонансе вторичный терминал C 2 может производить свободную энергию в нагрузке в некотором количестве, не более или равном мощности первичного генератора колебаний. Для извлечения большей мощности, в области осциллирующего электрического поля может быть установлено несколько одинаковых вторичных терминалов.
Электролиз, как работа потенциального поля по перемещению ионов
В 1888 году русский ученый Дмитрий А. Латчинов, изобретатель электролитического способа получения водорода, запатентовал высокоэффективный способ электролиза воды. Его способ демонстрировал парадоксальную ситуацию: электролитическая ячейка может производить газ высокого давления, но при этом требует такие же затраты электроэнергии, как и при производстве газа низкого давления. Вторичный эффект при работе электролизера высокого давления заключается в самоохлаждении электролитической ячейки, поскольку ей необходимо компенсировать избыточную выходную мощность за счет внутреннего тепла. Ранее этот способ не мог быть теоретически обоснован, поскольку он противоречил второму закону термодинамики, но сейчас существует много объяснений конверсии тепла в работу.
Можно сказать, что это был один из примеров теплового насоса, то есть технологии, которая связана с понятием синтропии, а не энтропии. Физически, механизм генерирования свободной мощности здесь заключается в том, что потенциальное поле между электродами перемещает ионы. Электрический ток проводимости, идущий через первичный источник, не является необходимым условием электролиза. Потенциальное поле само по себе уже производит разложение воды и поэтому выходная мощность может быть намного более, чем мощность, затраченная на создание потенциального поля.
Ускорение в потенциальном поле
Когда параметры поля или параметры рабочего тела меняются, то становится возможным создавать только ускорение тела в потенциальном поле. Примеры: Экранирование части траектории ротора позволяет использовать кулоновские силы только для ускорения ротора, патент США №4897592. Другой способ исключения отрицательной части работы состоит в пространственной суперпозиции источника поля и рабочего тела, Рис.3.
Некоторая аналогия позволяет объяснить известный эксперимент Александра Чернетского по созданию самогенерирующегося разряда, как использование работы потенциального поля. Небольшое демонстрационное устройство было изготовлено мной и показано в ходе конференции. Рассмотрим Рис.4
Профессор Александр Чернетский [5] объяснял полученные результаты эффектом пинчеванием тока в искре, что требует силы тока в сотни Ампер. В своем объяснении он использовал концепцию виртуальных частиц, возникающих на короткое время при эффекте поляризации вакуума, и отдающих часть своей энергии реальным частицам, согласно многочисленным теориям «энергии нулевой точки». Другое объяснение предлагается здесь: очевидно, что заряженная частица получает некоторую дополнительную кинетическую энергию в процессе своего движения, поскольку это движение является ускоренным, так как оно происходит в электрическом потенциальном поле между электродами, Рис.5.
Изменяющееся магнитное поле
Подвижная металлическая деталь устройства (экран) периодически изменяет конфигурацию поля в области между магнитами. По этой причине возникает периодическая сила взаимодействия, что создает мощность на выходе. Движение экрана, теоретически, вообще не требует затрат мощности, так как в идеальной конструкции экран входит в зазор с ускорением, а затем, с равным по силе торможением, выводится из зазора. Другой способ известен как «альтернатор», в котором ротор периодически вносит металлический элемент в зазор между постоянным магнитом и катушкой генератора.
Таким образом, периодическое изменение плотности энергии в точке извлечения мощности позволяет совершать полезную работу за счет постоянного магнитного поля.
Причина и два встречных следствия
при пространственном разделении
Простой пример двух пространственно разнесенных следствий одной причины показан в схеме на Рис. 7. 
Представляется возможным построить по такой схеме генератор с КПД более 100%, поскольку он, теоретически, имеет нулевой тормозящий эффект в данной двунаправленной схеме нагрузки. Можно надеяться, что в другой похожей схеме, при особой версии расположения ротора и катушек нагрузки, удастся получить ускорение ротора при подключении нагрузки в цепь вторичных катушек.
Внутренняя структура потенциального поля
Отсюда, мы полагаем, что мощность, получаемая за счет потенциального поля, может быть получена только благодаря дисбалансу внутренней структуры поля. Двунаправленный поток энергии, о котором мы говорили ранее, математически может быть представлен простым выражением
или в виде выражения
В новой формулировке закон сохранения энергии приобретает смысл закона сохранения баланса структуры времени: Энергия всех процессов в прямом времени должна быть равна энергии всех процессов в реверсированном времени.
Строение потока времени может быть более сложным, чем двунаправленное «время/реверсированное время» и хрональная область, как и пространственная область, может рассматриваться в многомерной форме.
1. PhReview E, vol.48, num.2, p.1562-1565, Extracting energy and heat from the vacuum; PhReview A, vol.39, num.5, Gravity as a zero-point-fluctuation force, Dr. Harold Puthoff. Patent: Electronic Devices Using Discreet, Contained Charge Particle Bundless and Source of Same, H.E.Puthoff, E.W. Church, Jr.,B.B.Clifton, S.R.Little patent number 5,208,844 of May 4, 1993.
3. Измерения токов проводимости, которые создаются посредством поляризационных токов, Заев Н.В., Авраменко С.В., Лисин В.Н., Русская Физическая Мысль, N 2, 1991, г. Реутов, Москва.
4. Nikola Tesla, Colorado Springs Notes 1899-1990, Publ. in Angriff Press, P.O.Box 2726, Hollywood, CA, 90078, USA.
5. Чернетский А.В., О физической природе биологических явлений и их моделировании, Москва, Изд. Политехнического Института, 1989.
6. On the Expression of the Electromagnetic Field due to Electrons by Means of Two Scalar Potential Functions, by E.T.Whittaker, 1903, Published in Proceedings of the London Mathematical Society, Vol.1, 1904, p.367-372. Also it is included in Annex C, Gravitobilogy, T.E.Bearden, p. c-1.
7. Gravitobiology, by T.E.Bearden, 1991, Tesla Book Company, P.O.Box 121873 Chula Vista, CA 91912, USA. Library of Congress Catalog Card Number 86-50553.
Copyrights 2015 © Alexander V. Frolov +7 (910) 9482509 Skype alexfrolov2509
Работа в потенциальном поле
При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении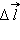 
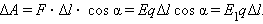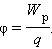
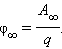
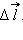равна (рис. 1.4.1):
 |
Работа Δ A кулоновских сил на этом перемещении равна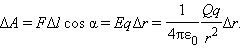
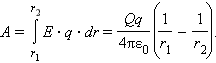
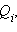то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ 
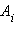кулоновских полей точечных зарядов: 
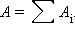Так как каждый член суммы 
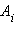не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.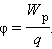
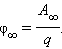
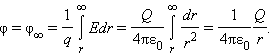
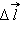вдоль силовой линии из точки (1) в точку (2), то можно записать: