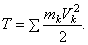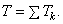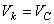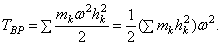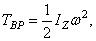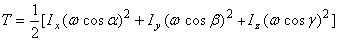потенциальное поле это физика
Потенциальное поле
Смотреть что такое «Потенциальное поле» в других словарях:
потенциальное поле — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN potential field … Справочник технического переводчика
потенциальное поле — potencialinis laukas statusas T sritis Standartizacija ir metrologija apibrėžtis Potencialinės jėgos, išreikštos skaliarine funkcija – potencialo gradientu, laukas, pvz., elektrostatinis laukas. atitikmenys: angl. potential field vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
потенциальное поле — potencialinis laukas statusas T sritis Standartizacija ir metrologija apibrėžtis Skaliarinio potencialo laukas. atitikmenys: angl. potential field vok. Potentialfeld, n rus. потенциальное поле, n pranc. champ potentiel, m … Penkiakalbis aiškinamasis metrologijos terminų žodynas
потенциальное поле — potencialinis laukas statusas T sritis fizika atitikmenys: angl. potential field vok. potenzielles Feld, n rus. потенциальное поле, n pranc. champ potentiel, m … Fizikos terminų žodynas
Потенциальное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве … Википедия
векторное потенциальное поле — vektorinis potencialinis laukas statusas T sritis radioelektronika atitikmenys: angl. vector potential field vok. Potentialfeld, n; Vektorpotentialfeld, n rus. векторное потенциальное поле, n pranc. champ vectoriel à potentiel, m … Radioelektronikos terminų žodynas
векторное потенциальное поле — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN vector potential field … Справочник технического переводчика
Потенциальное векторное поле — Потенциальное (или безвихревое) векторное поле в математике векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном… … Википедия
потенциальное силовое поле — Силовое поле, для которого существует силовая функция. Примечание. Силы в этом силовом поле называются потенциальными силами. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической… … Справочник технического переводчика
Потенциальность электростатического поля
Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.
Что такое потенциальное поле
Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).
Известно, что сила гравитации F G
На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.
Легко докажем это математически. Циркуляция вектора напряженности поля точечного заряда E i → по любому замкнутому контуру равняется 0 :
Если поле создает N точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:
Что такое ротор. Практические задачи
Ротор − это вектор, проекция которого на направление единичного вектора n → определяется таким образом:
Обращаем внимание, что в формуле большой буквой S обозначена площадь, а маленькой буквой s − линейное перемещение.
Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:
Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:
где L 1 и L 2 − это различные пути между точками А и В . При замене местами пределов интегрирования получаем:
Выражение ∫ A L 1 B E → · d s → = ∫ A L 2 B E → · d s → представим в виде:
к уравнению выше, получаем:
Это дифференциальная формулировка потенциальности электростатического поля.
Необходимо найти r o t n υ → для точек оси вращения, если υ → − это вектор скорости точек твердого тела, вращающегося с угловой скоростью ω вокруг оси коллинеарной n →
Решение
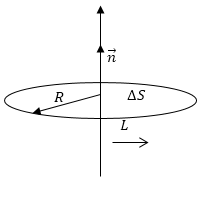
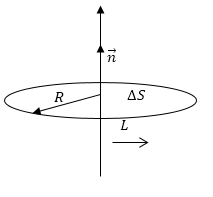
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок 1 ). Известно, что:
где ∮ d s = 2 π R − это длина окружности.
Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.
Решение
Поскольку электростатическое поле потенциально, тогда выполняется равенство:
Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.
Потенциальность электростатического поля
Вы будете перенаправлены на Автор24
Что такое потенциальное поле
Поле (для любых сил) называется потенциальным (консервативным), если работа при перемещении в нем зависит только от конечной и начальной точки пути и не зависит от траектории движения тела. Существует и другое, но абсолютно равнозначное определение потенциальности поля. Поле называется потенциальным, если при перемещении по любому замкнутому контуру работа сил поля равна нулю.
Нам известно, что сила гравитации ($F_G\sim \frac<1>
На основании принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля. Математически доказать это очень просто. Циркуляция вектора напряженности поля точечного заряда ($\overrightarrow
Если поле создается N точечными зарядами, то по принципу суперпозиции мы можем результирующее поле найти как:
Выше описанный критерий потенциальности поля не является дифференциальным, вследствие чего, его бывает трудно применять. Приходится проверять равенство нулю работы по замкнутому контуру. Это значит необходимо исследовать бесконечное количество циклов, что, в конечном счете, невозможно. Критерий потенциальности можно применить только тогда, когда известна аналитическая формула работы, что бывает совсем не всегда. Следовательно, необходимо найти другой критерий потенциальности поля, который был бы легок в применении. Таким критерием стала дифференциальная формулировка. Она дается с помощью понятия ротор вектора ($rot\overrightarrow$).
Что такое ротор
Ротор характеризует интенсивность «завихрения» вектора. При практическом вычислении ротора используют формулы:
Независимость работы от пути перемещения заряда в электростатическом поле выражается равенством:
Выражение (6) представим как:
к уравнению (8), получим:
\[\oint\limits_L<\overrightarrow>=\int\limits_S>=0\ \left(9\right),\]
Формула (10) является дифференциальной формулировкой потенциальности электростатического поля.
Готовые работы на аналогичную тему
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рис.1). Мы знаем, что:
\[v=\omega R\left(1.1\right),\] \[\triangle S=\pi R^2\left(1.2\right).\]
Задание: Доказать, что из условия потенциальности поля следует, что тангенциальные составляющие напряженности электростатического поля не прерываются.
Так как электростатическое поле потенциально, то выполняется равенство:
Потенциальное поле это физика
Чрезвычайно большое значение в физике имеют векторные поля, для которых тождественно равпа нулю либо дивергенция, либо ротация, либо и та и другая величины вместе. Изучением этих полей мы и займемся.
§ 1. Потенциальное поле
1. Потенциальное поле как безвихревое поле.
Векторное поле В называется потенциальным, если в каждой его точке ротация равна нулю:
Потенциальное поле называют также безвихревым полем.
Примером потенциального поля может служить электростатическое поле Е (см. гл. XVIII, § 1).
2. Поле градиента.
Рассмотрим произвольное скалярное поле
В каждой точке этого поля единственным образом определяется градиент поля
Следовательно, каждому скалярному полю соответствует определенное векторное поле — поле градиента.
Найдем ротацию поля градиента какой-либо скалярной функции:
Теорема. Поле градиента любой скалярной функции есть поле потенциальное:
Потенциальное поле сил



Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения части
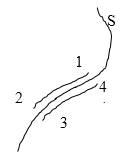
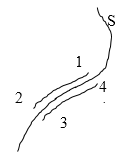
Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными (сила трения). Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части: 1а2 и 2b1. Так как поле
 |
| Рис. 5.5. Работа в потенциальном поле сил |
потенциально, то, по условию 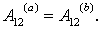
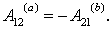
что и требовалось доказать.
Наоборот, если работа сил поля на любом замкнутом пути равна нулю, то и работа этих сил на пути между произвольными точками 1 и 2 от формы пути не зависит, т. е. поле потенциально. Для доказательства выберем два произвольных пути: 1а2 и 1b2 (рис. 5.5). Составим из них замкнутый путь 1a2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. 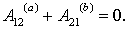
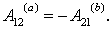
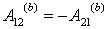
Введем понятие потенциальной энергии частицы в поле. То, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.
Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек P в фиксированную точку O. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки P (при фиксированной точке O ). А это значит, что данная работа будет некоторой функцией радиус-вектора r точки P.
Обозначив эту функцию 
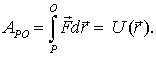 | (5.9) |
Функцию 
Ранее было показано, что при перемещении частицы из одной точки потенциального поля в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы, т. е. 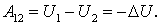
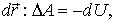
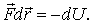 | (5.14) |
Учитывая, что 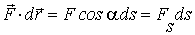
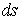
где 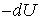
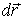
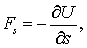 | (5.15) |
Перемещение 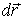
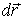
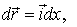
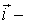
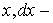
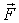
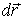
где 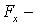
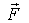
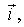
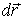
Подставив последнее выражение в уравнение (5.14), получим
где символ частной производной означает, что потенциальная энергия 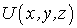
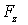
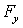
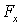
Итак, взяв с обратными знаками частные производные функции U по х, у и z, мы найдем проекции 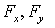
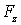
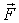

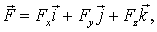
Величину, стоящую в скобках, называют градиентом (полным дифференциалом) скалярной функции U и обозначают 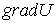

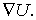
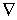
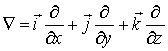
Т.о., сила, действующая на точку со стороны силового поля, выража-
ется через градиент потенциальной энергии точки в этом поле, взятый
с обратным знаком. Т.е. сила оказывается направленной в сторону наи-
быстрейшего убывания потенциальной энергии.
7.Нормировка потенциальной энергии.
Потенциальная энергия принимается равной нулю для некоторой конфигурации (координат) тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии. 
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
| |
|
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
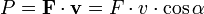 |
F — сила, v — скорость, α — угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
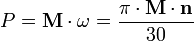 |
M — момент силы, 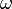
2. Энергия системы материальных точек.
Кинетическая энергия системы.
Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы
Кинетическая энергия является характеристикой и поступательного и вращательного движения системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:
Кинетическая энергия – скалярная и всегда положительная величина.
Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.
1. Поступательное движение.
В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки
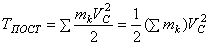
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит.
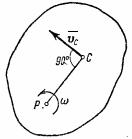
2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рис.46), то скорость любой его точки 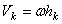
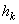
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:
т. е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.
При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.47)
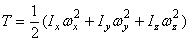
где Ix, Iy, Iz – моменты инерции тела относительно главных осей инерции x1, y1, z1 в неподвижной точке О ; 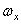
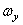
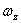
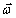
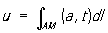









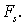
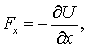
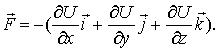

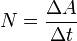 — средняя мощность
— средняя мощность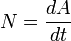 — мгновенная мощность
— мгновенная мощность