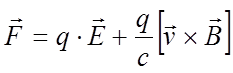полупроводники в магнитном поле

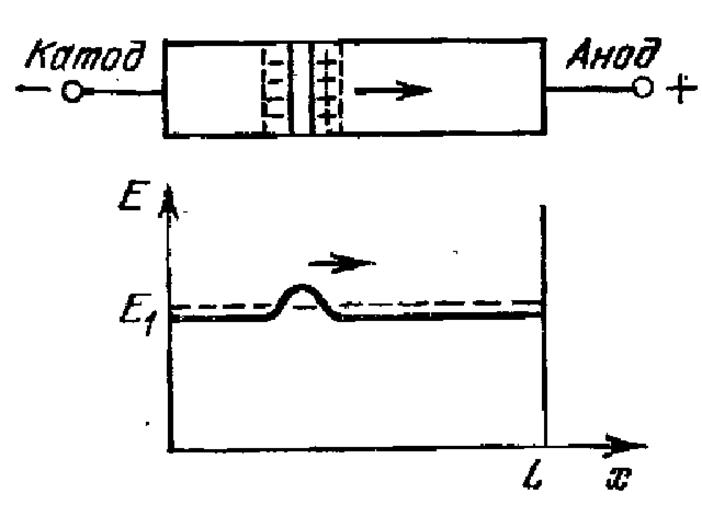
Рис. 6.8. Распределение поля и заряда внутри домена, поясняющее эффект Ганна.

Эффект Ганна применяется в диодах Ганна, использующихся для генерации СВЧ колебаний.

Лекция 15. Полупроводники в магнитном поле.

Эффект Холла. Тензор магнитосопротивления. Холловская подвижность. Квантование электронов и дырок в сильном магнитном поле. Уровни Ландау. Циклотронный резонанс. Квантовый эффект Холла.

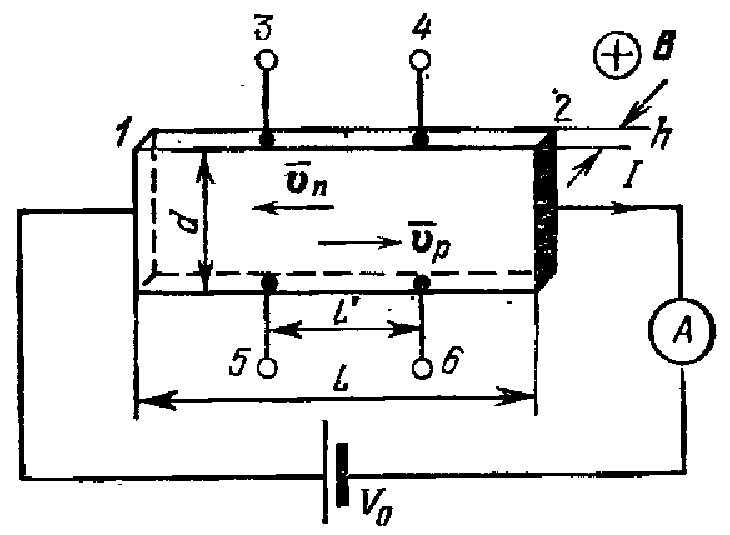
Рассмотрим схему измерений, похожую на ту, что использовалась для измерения удельного сопротивления. Контакты 1 и 2 – токовые контакты, контакты 3-6 потенциальные контакты. В отсутствии магнитного поля, если наш образец однороден по сопротивлению, при пропускании тока через него, падение напряжения между контактами 3 и 5 равно нулю (как и между контактами 4 и 6). В 1879 году, американский физик Э.Холл обнаружил, что если приложить перпендикулярно к образцу магнитное поле, между контактами 3-5 возникает напряжение (Э.Д.С. Холла), пропорциональное току, протекающему через образец. Рассмотрим причины данного эффекта, названного по имени первооткрывателя эффектом Холла.

Рис. 6.9. Схема измерения эффекта Холла.

В постоянных электрическом и магнитном полях на заряженную частицу действует сила Лоренца.

Рассмотрим полупроводник с электронным типом проводимости, концентрация дырок в котором пренебрежимо мала, поэтому их вкладом в ток можно пренебречь. Скорость движения электронов состоит из хаотической тепловой и дрейфовой. В силу линейности силы Лоренца от скорости 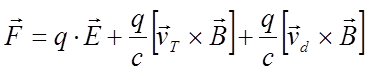. Так как в среднем тепловая скорость равна нулю, то средняя сила зависит только от дрейфовой скорости. Установившийся (после включения магнитного поля) в образце ток течёт слева направо (рис. 6.9), вертикальной компоненты у тока нет. Это происходит из за того, что магнитная составляющая силы Лоренца уравновешивается силой, возникающей из-за Э.Д.С. Холла:

(6.9)

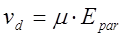
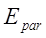
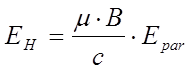
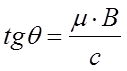
Выразим дрейфовую скорость из формулы 6.7 , где — компонента напряжённости электрического поля, параллельная току. Тогда:

(6.10)

При измерении эффекта Холла важно правильно выбрать геометрию образца и контактов. Металлические контакты 1 и 2 – эквипотенциали на краях образца, на рисунке 6.9 они вертикальны, тогда как в глубине, у контактов 3-6, эквипотенциали наклонены на угол q. Поэтому, для уменьшения искажений, вносимых токовыми контактами, их необходимо удалить от потенциальных контактов. 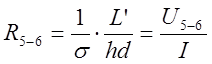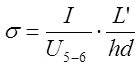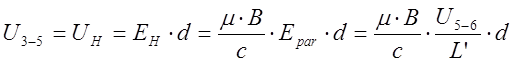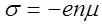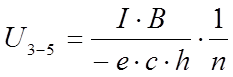Если угол q мал, то сопротивление образца между контактами 5 и 6 равно: , тогда, можно найти удельную проводимость: . Измеряемая экспериментально Холловская Э.Д.С. равна: . Отсюда подвижность . То есть, измеряя Э.Д.С. Холла можно определить подвижность носителей заряда. Теперь определив подвижность и проводимость, используя можно определить связь между концентрацией носителей заряда и Э.Д.С. Холла:

(6.11)

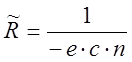
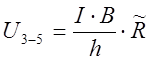
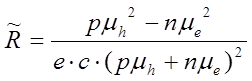
знак Э.Д.С. Холла направлением магнитного поля и знаком носителей заряда. Постоянную называют коэффициент Холла, или постоянная Холла: . Попробуйте самостоятельно получить, что при учёте дырок с концентрацией p, постоянная Холла равна:

(6.12)

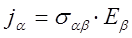
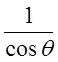
Как уже отмечалось, влияние магнитного поля приводит к тому, что направлением тока становится не параллельно направлению электрического поля. Проводимость становится тензором: . Удельное сопротивление также становится тензором, в этом случае говорят о тензоре магнитосопротивления. Чтобы точно найти тензор удельного сопротивления (и обратный ему тензор удельной проводимости) нужно найти движение заряженной частицы в скрещенных электрическом и магнитном полях с учётом конечной вероятности её рассеяния (обратно пропорциональной времени релаксации по импульсу). Затем надо усреднить скорость по всему ансамблю частиц, с учётом того что время релаксации зависит от энергии (и от скорости) частицы [2.3]. Качественно, результат заключается в следующем. Недиагональные члены тензора проводимости будут пропорциональны магнитному полю. Диагональные члены тензора проводимости будут чуть меньше, чем в случае отсутствия магнитного поля. Ведь теперь, чтобы сместиться вдоль поля E, частица должна проделать путь больший в раз.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Микроминиатюризация: магнитный полупроводник толщиной в два атома

Со времен первых сотовых телефонов, которые весили до одного килограмма и работали от силы пол часа без подзарядки, в мире технологий произошло множество полезных усовершенствований, новаторских изобретений и революционных открытий. С течением времени гаджеты, которые мы используем практически каждый день, становятся меньше в габаритах, но больше в аспекте производительности. Этот процесс неминуемо движется в тупик, поскольку классические транзисторы не могут уменьшаться бесконечно, что бы там не требовали дизайнеры новых смартфонов или планшетов. Следовательно, нужно отказаться от классики и создать нечто совершенно новое, что и сделали ученые из технологического института Стивенса (США). Сегодня мы рассмотрим исследование, в котором они описывают атомарно тонкий магнитный полупроводник, способный не только использовать заряд электрона, но и его спин. Что легло в основу нового полупроводника, как он был создан, и насколько производительна эта революционная новинка? Об этом нам расскажет доклад ученых. Поехали.

Основа исследования

Спин это собственный момент импульса элементарных частиц. Спинтроника в свою очередь является разделом квантовой электроники, которая занимается изучением спинового токопереноса в твердотельных веществах. Другими словами, в отличие от классической электроники, в спинтронике перенос информации происходит посредством тока спинов.

В аспекте создания новых устройств многие ученые стараются получить полный контроль над спин-поляризованными носителями заряда. Одним из вариантов достижения этой цели является разбавленный магнитный полупроводник (РМП или DMS от dilute magnetic semiconductors). Обычный магнитный полупроводник объединяет в себе свойства ферромагнетиков и полупроводников. А вот разбавленный (или полумагнитный полупроводник) по сути является немагнитным полупроводником, в который внедрили определенное число парамагнитных атомов. К примеру, легирование элементов переходных металлов, таких как железо (Fe) и марганец (Mn), в немагнитные объемные полупроводники позволяет получить DMS.

Относительно недавнее открытие ферромагнетизма в двумерных (2D) атомарно тонких слоях, таких как CrI₃ (трийодид хрома) и Cr₂Ge₂Te₆ (теллурид хрома-германия) сместило акцент исследований от объемных кристаллов к двумерным материалам.

Монослои дихалькогенидов переходных металлов (ДПМ)* в виде атомарно тонких полупроводников демонстрируют уникальные электрические и оптические свойства, которые напрямую зависят от толщины. Однако монослои ДПМ остаются немагнитными в своей собственной форме.

Дихалькогениды переходных металлов (ДПМ)* — это тонкий монослойный полупроводник, состоящий из переходного металла и халькогена (кислорода, серы, селена, теллура, полония или ливермория). Один слой атомов металла располагается между двумя слоями атомов халькогена, что можно выразить формулой MX2 (М — металл и Х — халькоген).

Легирование ДПМ, таких как ванадий (V), Mn и Fe, и преобразование его в атомарно тонкий разбавленный магнитный полупроводник (РМП) позволило бы исследовать магнитную связь в двухмерных ограниченных структурах. Несмотря на то, что ДПМ ограничены растворимостью и химической стабильностью, они могут быть в некоторой степени легированы в однослойные РМП. Тем не менее, в ходе таковых экспериментов ферромагнетизм не был продемонстрирован.

Несмотря на это, 2% Mn легирование в монослоях Mn:MoS₂, выращенных на графеновой подложке, и 1% рений (Re) легирование в монослое Re:MoS₂ продемонстрировали подавление эмиссии при низких температурах, связанной с дефектами. Следовательно, есть шанс полноценно реализовать монослойные ДПМ.

Ранее уже проводились исследования, в которых ученые пытались реализовать столь сложную задачу, как разбавленный магнитный полупроводник на основе ДПМ, но результаты этих трудов были не особо удовлетворительны.

В рассматриваемом нами сегодня исследовании все же удалось достичь положительного результата в виде успешного замещающего легирования атомов Fe в монослои MoS₂.

Результаты исследования

Легирование железом (Fe) монослоя MoS₂ осуществлялось путем выращивания MoS₂ и Fe₃O₄ методом химического осаждения из газовой фазы.

Чтобы устранить эффекты локальных деформаций в субстрате, монослои MoS₂ и Fe:MoS₂ были инкапсулированы в тонкопленочный hBN (гексагональный нитрид бора).

Изображение №1

На изображении 1а показан РЭМ (растровый электронный микроскоп) снимок монослоев Fe:MoS₂. Мы видим треугольные островоподобные домены, что вполне типично для подобных методов синтеза MoS₂.

Изображение 1b показывает схематическое представление атомных структур монослоев Fe: MoS₂ (вид сверху и сбоку). Поскольку замещение атомами Fe участков Мо является термодинамически благоприятным (т.е. реакция не требует энергии, чтобы произойти), один атом легирующей примеси Fe заменяет один атом Mo в кристалле MoS₂.

На 1с показан ПРЭМ (просвечивающий растровый электронный микроскоп) снимок монослоя Fe: MoS₂. По сравнению с атомами Мо (Z = 42), Fe (Z = 26) имеет атомный номер (т.е. зарядовое число — количество протонов в атомном ядре) на 40% меньше. Поскольку величина интенсивности рассеянных электронов зависит от атомного номера, ожидалось, что атомы Fe будут вырабатывать более низкую относительную интенсивность, что отчетливо видно для замещенных атомов Fe на ПРЭМ снимке.

Соответствующее ПРЭМ сканирование интенсивности (1d) указывает на то, что коэффициент интенсивности равен 0.38, что согласуется с ранее проведенными исследованиями.

Для точного подтверждения роста монослойных доменов Fe:MoS₂, образцы были проверены с помощью атомно-силовой микроскопии (АСМ). Данная методика позволила подтвердить, что после влажной очистки и термического отжига на поверхности Fe:MoS₂ не содержится каких-либо частиц Fe3O4, оставшихся там после легирования.

Изменения в решетке монослоя были дополнительно изучены посредством сравнения спектров фотолюминесценции при комнатной температуре монослоев MoS₂ и Fe:MoS₂. Наблюдаемое сильное гашение фотолюминесценции объясняется дополнительными безызлучательными каналами рекомбинации (состояниями захвата), которые обусловлены легированием, что подтверждает успешное внедрение Fe. Эволюция интенсивности фотолюминесценции в зависимости от температуры для монослоев Fe:MoS₂ и MoS₂ показана на 1e и 1f соответственно.

Изображение №2

На изображении 2а показана низкотемпературная фотолюминесцентная (ФЛ) эмиссия монослоев Fe:MoS₂ и MoS₂ в более широком диапазоне энергий, в том числе и в режиме запрещенной зоны. При сравнении ФЛ монослоев Fe:MoS₂ и MoS₂ становится очевидным пик излучения при 2.28 эВ.

На графике 2b показано излучение Fe:MoS₂ для трех различных треугольников, демонстрирующее значительные изменения интенсивности на пике 2.28 эВ. Причиной этих изменений может быть разница в концентрации легирующей примеси (Fe) между этими разноориентированными треугольниками.

Далее, чтобы исключить связанные с Fe локальные колебательные рамановские моды в качестве источника электронно-дырочного перехода*, были записаны оптические спектры в области пика 2.28 эВ. При этом длина волны лазера регулировалась от 405 нм (2c) до 532 нм (2d).

Электронно-дырочный переход* — участок соприкосновения двух полупроводников с разной проводимостью — дырочной (положительной) и электронной (отрицательной).

Сравнение результатов показало, что положение пика не меняется. Это подтверждает, что наблюдаемое излучение, связанное с железом, не вызвано рамановской колебательной модой, которая бы сдвигалась относительно энергии лазера.

Изображение №3

Чтобы исследовать происхождение пика ФЛ, связанного с железом, при 2.28 эВ, исследователи использовали DFT (теорию функционала плотности) для расчета электронной структуры Fe:MoS₂.

Изолированная легирующая примесь Fe была смоделирована в виде замены одного атома Mo на атом Fe в 5х5 суперячейке MoS₂ (3а).

На 3b показана структура спин-поляризованных зон для этой системы, где площадь каждого синего (или зеленого) круга пропорциональна перекрытию состояния со спином вверх (или вниз) и сферы радиусом 1.3 Å с центром в атоме Fe. График показывает, что присутствие Fe вводит состояния, которые лежат внутри нетронутой запрещенной зоны MoS₂. А тот факт, что большие синие и зеленые круги внутри запрещенной зоны не перекрываются, указывает на то, что Fe индуцирует магнитный момент.

На графике 3с показано сравнение скоростей спонтанного излучения зоны проводимости со спином вверх и зоны проводимости нетронутого MoS₂. Наименьшая энергия излучения для первоначального состояния MoS₂ составляет

1.79 эВ, что соответствует большому пику ФЛ на 2а, который возникает в результате релаксации по всей ширине запрещенной зоны. Присутствие Fe вводит еще один значительный переход с энергией

2.32 эВ, что соответствует экспериментально наблюдаемому пику ФЛ эмиссии Fe:MoS₂ при 2.28 эВ.

Ожидаемая величина пика ФЛ намного меньше, чем показано на 3с, поскольку любая дырка в валентной зоне, оставшаяся от лазерного возбуждения, очень быстро релаксирует без излучения до максимума валентной зоны. Поэтому дырки будут проводить очень мало времени в состоянии валентной зоны, соответствующем переходу 2.28 эВ, что делает этот переход гораздо менее вероятным, чем переход до максимума валентной зоны.

Изображение №4

На следующем этапе исследования была проведена оценка магнитных характеристик монослоев Fe:MoS₂.

Известно, что оптическое излучение от комплексов ионов переходных металлов обычно возникает в результате переноса заряда между лигандами и переходным металлом. Спиновый угловой момент электрона в ионе сильно зависит от поляризации из-за правил отбора спина циркулярно поляризованного света. Таким образом, ионы переходных металлов демонстрируют неодинаковое количество поглощения света при возбуждении с левой и правой круговой поляризацией.

На атомном уровне поглощение света тесно связано с магнитоиндуцированными зеемановскими сдвигами. Следовательно, выполнение MCD-спектроскопии (магнитный круговой дихроизм) может дать представление о магнитных свойствах материала.

Графики 4а и 4b показывают ФЛ спектры Fe:MoS₂ при возбуждении противоположным циркулярно поляризованным светом как при 4 K, так и при комнатной температуре. Излучение, связанное с Fe, показывает сильный круговой дихроизм* (ρ ≈ 40%) как при 4 K, так и при RT.

Круговой дихроизм* — различие между коэффициентами поглощения света, поляризованного по правому и левому кругу.

Учитывая, что свечение переходных металлов теряет свой круговой дихроизм выше температуры Кюри, наблюдение сильного дихроизма при 300 K предполагает, что Fe:MoS₂ остается ферромагнитным при комнатной температуре.

На графике 4с показана связанная с Fe эмиссия MCD в зависимости от возрастающего (синие точки) и уменьшающегося (красные точки) магнитного поля в диапазоне от −3 Т до 3 Тл при 4 К. Ярко выраженная петля гистерезиса четко идентифицирует ферромагнитную природу излучения ФЛ, связанного с железом.

На 4d видно, что монослои Fe:MoS₂ демонстрируют выраженную петлю гистерезиса M – H как при 5 К, так и при комнатной температуре. Это подтверждает, что синтезированные монослои Fe:MoS₂ демонстрируют ферромагнетизм даже при 300 К.

В заключение ученые провели магнитометрию монослоев Fe:MoS₂ для оценки локальной силы ферромагнитного поля при комнатной температуре методом ODMR (оптическое детектирование магнитного резонанса).

Изображение №5

Примерный спектр ODMR для Fe:MoS₂ и MoS₂ показан на 5а. На 5b показана гистограмма зеемановских расщеплений энергии, записанных в 24 и 20 различных точках монослоя Fe:MoS₂ и нелегированного MoS₂ соответственно. Статистический анализ показывает, что среднее расщепление энергии на Fe:MoS₂ увеличилось на

11 МГц по сравнению с чистым MoS₂. Из этих данных удалось установить, что локальное магнитное поле образца может достигать 0.5 ± 0.1 мТл. Этот показатель близок к измеренным в 2D-ферромагнетиках CrI₃ и CrBr₃ при криогенной температуре.

Тот факт, что Fe: MoS₂ демонстрирует большое локальное магнитное поле при комнатной температуре, является четким свидетельством того, что этот материал сохранил свою намагниченность. Следовательно, из данных можно сделать вывод, что монослои Fe:MoS₂ с внедренными атомами Fe действуют как разбавленные магнитные полупроводники, демонстрирующие ферромагнетизм при комнатной температуре.

Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.

Эпилог

Развитие технологий и соответствующих устройств часто сопряжено с комфортом тех, кто ими будет пользоваться. Современные устройства становятся все миниатюрнее, но компактности много не бывает. Однако, как бы пользователи ни желали минимизировать габариты любимых гаджетов, этот процесс ограничен размерами внутренностей этих устройств.

Авторы сего исследования отмечают, что классические транзисторы не могут уменьшаться бесконечно, что вполне соответствует как законам логики, так и физики. Тем не менее, если классика не работает, то можно обратить свой взор в сторону модерна, что и сделали ученые. В своем труде они описали новый тип полупроводника Fe:MoS₂, объединяющем в себе свойства полупроводника и ферромагнетика. В процессе его создания атомы железа так сказать выталкивают атомы молибдена, занимая их место. Результатом этого процесса является очень тонкий (всего два атома в толщину) и гибкий материал, сохраняющий намагниченность при комнатной температуре.

Как говорят сами исследователи, их изобретение не подчиняется известному многим закону Мура, поскольку оно не связано с физическим масштабированием. В своем труде они описали возможность использовать не только заряд электрона, но и его спин, что расширяет возможности будущих технологий.

Фундаментом устройств будущего, гибких, легких и прозрачных, по мнению ученых, может быть полное понимание и контроль свойств материалов, из которых они будут сделаны.

Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. 🙂

Немного рекламы 🙂

Источник

Гальваномагнитные эффекты в полупроводниках

Гальваномагнитными эффектами в полупроводниках называются такие явления, которые возникают при одновременном действии на полупроводник электрического и магнитного полей.

Все гальваномагнитные эффекты делятся на поперечные (действие электрического и магнитного полей обнаруживается на гранях полупро­водника, параллельных электричес­кому и магнитному полям) и продоль­ные (проявляются вдоль образца).

К поперечным относятся эффекты Холла и Эттинсгаузена, к параллель­ным—изменение сопротивления образ­ца в магнитном поле и эффект Нернста (продольная разность температур).

Рассмотрим только эффект Холла. Если полупроводник, вдоль которого течет электрический ток, поместить в магнитное поле, перпендикулярное

направлению тока, то в полупроводнике возникнет поперечное электрическое поле, перпендикулярное току и магнитному полю. Это явление получило название эффекта Холла, а возникающая по­перечная ЭДС — ЭДС Холла.

На рис. 8.8 изображена пластинка полупроводника n-типа. Электрическое поле Е направлено параллельно оси Z, а магнитное

поле Н — вдоль оси У. На движущийся в магнитном поле электрон действует сила Лоренца, которая отклоняет его в направлении, перпендикулярном направлению магнитного поля. В результате электроны будут накапливаться у одного из торцов образца. На противоположной грани будет создаваться положительный нескомпенсированный заряд, обусловленный ионами донорной приме­си. Такое накопление зарядов будет происходить до тех пор, пока действие возникшего в результате такого процесса электрического поля не уравновесит действующую на электрон силу Лоренца. Ус­ловие равновесия действующей на электрон силы в скалярной фор­ме можно записать в виде

где Vn — средняя скорость направленного движения электрона;

В — магнитная индукция в образце; Ex — напряженность воз­никшего поперечного электрического поля.

Считая поперечное электрическое поле однородным, получим

где а — ширина пластинки; Ux — ЭДС Холла. Известно также, что j = сигмаЕ или

Используя (8.24), из (8.22) получаем

Величина Rx называется коэффициентом Холла и определяется

ЭДС Холла в полупроводнике n-типа можно определить по формуле

Знак минус отражает тот факт, что носителями заряда в данном полупроводнике являются электроны. Для полупроводников р-типа получается аналогичное выражение, только лишь концентра­ция п будет заменена на р и направление поперечного электрическо­го поля будет противоположным, т. е. ЭДС Холла будет положи­тельная. Это обстоятельство используется для определения типа электропроводности полупроводников.

Если выразить ток в А, напряженность магнитного поля — в А/м, холловское напряжение — в В, толщину образца — в см, то коэффициент Холла равен (cm 3 /k)

Таким образом, измерив разность потенциалов Холла Ux при из­вестном токе I, напряженности магнитного поля Н и толщине образ­ца b рассчитываем Rx. Далее, если известны коэффициент Холла Pх и электропроводность, легко вычислить концентрацию носителей заряда и величину подвижности.

Эффект Холла интересен не только как метод определения харак­теристик полупроводниковых материалов, но и как принцип дейст­вия целого ряда полупроводниковых приборов, нашедших техниче­ское применение.

Основным элементом структуры большинства типов полупровод­никовых приборов является электрический переход- переходный слои в полупроводниковом материале между двумя областями с раз­личными типами электропроводности или разными значениями

удельной электропроводности, причем одна из областей может быть металлом.

Электрический переход между двумя областями полупроводни­ка. одна из которых имеет электропроводность р-типа, а другая —

n-типа, называют электронно-дырочным переходом или р-п-переходом.

Сооздать р-n-переход механическим соединением двух полупро­водников с различным типом электропроводности невозможно электронно-дырочные переходы получают путем введения в полупроводник донорной и акцепторной примесей таким образом, чтобы одна часть полупроводника обладала электронной, а другая — ды­рочной электропроводностью.

Рассмотрим две отдельно взятые области электронного и ды­рочного полупроводников, показанные на рис. 8.9, а. Основные но­сители заряда в полупроводнике n-типа — электроны (на рис. 8.9,о обозначены знаком минус), а в полупроводнике р-типа—дырки (на рис. 8.9, а обозначены знаком плюс). Ионизированные атомы донорной и акцепторной примеси обозначены соответственно знака­ми плюс и минус в кружочках. Неосновные носители в электрон­ном и дырочном полупроводниках не обозначены, так как их кон­центрация очень мала в сравнении с концентрацией основных носи­телей.

Условно будем считать, что п- и р-полупроводники приведены в идеальное соприкосновение (рис. 8.9. б). Так как в n-полупроводнике много электронов, а в р- полупроводнике много дырок, между полупроводниками начнется интенсивный обмен носителями заря­да. За счет разности концентраций электроны из полупроводника n-типа диффундируют в полупроводник р-типа, оставляя в приконтактной области полупроводника n-типа нескомпенсированный по­ложительный заряд ионов донорной примеси. Дырки, в свою очередь,

При смене полярности внешнего напряжения электрическое по­ле объемных зарядов и внешнее поле будут совпадать по направле­нию. В результате действия суммарного электрического поля ос­новные носители будут двигаться от перехода и пересечь переход смогут только неосновные носители. Так как количество неоснов­ных носителей во много раз меньше основных, то и ток, ими обу­словленный, будет мал по сравнению с тем, который получится при прямом включении. При данном включении электронно-дыроч­ный переход «заперт» и через него может протекать только малый обратный ток неосновных носителей.

На рис. 8.10 показана зависимость между током, текущим через р-п-переход, и внешним напряжением, которая называется вольт-амперной характеристикой. Описывается вольт-амперная характе­ристика р-n-перехода следующим выражением:

I = Is (e qU/(kT) –1) (8.29)

где Is — ток насыщения (при обратном включении р-п-перехода этот ток равен обратному току); U — приложенное напряжение;

Простые полупроводники

a) Германий. Германий—один из наиболее тщательно изучен­ных полупроводников, и многие явления, характерные для полу­проводников, впервые экспериментально были обнаружены на этом материале.

Существование и основные свойства германия предсказал Д. И. Менделеев в 1870 г. назвав его экасилицием. В 1886 г. немец­кий химик К. Винклер обнаружил в минеральном сырье новый элемент, который он назвал германием. Германий оказался эквива­лентен экасилицию. Содержание германия в земной коре невелико, но встречается он в естественных условиях во многих частях света. Выделяют германий из германийсодержащей руды чаще всего в ре­зультате химической переработки сырья с помощью концентриро­ванной НСL в виде тетрахлорида германия GeCL₄. Тетрахлорид гер­мания — летучая жидкость, которую подвергают глубокой очист­ке, используя методы экстракции и ректификации. После очистки GeCl₄ его гидролизуют водой, в результате чего получается диоксид германия GeO₂ — порошок белого цвета. После просушки GeO₂, восстанавливается в токе очищенного водорода при температуре 650 °С до элементарного германия, представляющего собой серый порошок. Восстановленный таким образом германий подвергается травлению в смеси кислот и его сплавляют в слитки. Слитки ис­пользуют в качестве исходного материала для получения особо чи­стого германия методом зонной плавки или же непосредственного получения монокристаллов методом вытягивания из расплава.

Сущность метода зонной плавки заключается в том. что узкая расплавленная зона перемещается вдоль горизонтально располо­женного образца, находящегося в графитовой или кварцевой ло­дочке. Примеси, имеющиеся в образце, оттесняются к концу слитка. Для высококачественной очистки весь процесс повторяют много раз или используют установки более совершенной конструкции, позволяющие создавать вдоль слитка одновременно четыре или пять расплавленных зон.

или поднимать для подбора оптимального положения тигля с расплавом по отношению к нагревательному элементу В. В каче­стве нагревательного элемента используют обычно печь сопротивле­ния или источник индукционного высокочастотного нагрева. Через верхний фланец камеры соосно с нижним штоком Б-1 вводится верхний шток Б-2, на нижнем конце которого крепится монокри­сталлическая затравка кристаллизуемого материала. Затравка вво­дится в расплав и выдерживается в нем, пока не произойдет оплав-ление поверхности. Когда это про­изойдет, затравку, вращая, начи­нают медленно поднимать. За за­травкой тянется жидкий столбик расплава, удерживаемый поверх­ностным натяжением. Попадая в область низких температур над поверхностью тигля, расплав за­твердевает, образуя одно целое с затравкой. Этим способом в насто­ящее время получают монокри­сталлы германия диаметром до 100 мм, а иногда и более.

химически устойчив на воздухе при комнатной температуре. Раз­мельченный в порошок германий при нагревании на воздухе до тем­пературы примерно 700 °С легко образует диоксид германия GеО₂. Герма­ний слабо растворим в воде и практически нерастворим в соляной и разбавленной серной кислоте. Активными растворителями гер­мания в нормальных условиях является смесь азотной и плавиковой кислот и раствор перекиси водорода. При нагревании германий ин­тенсивно взаимодействует с галогенами, серой и сернокислыми сое­динениями.

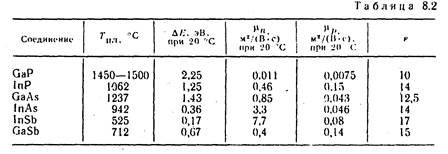
Основные физические свойства германия, кремния и селена при­ведены в табл. 8.1.

Температурные зависимости удельного сопротивления германия при различном содержании донорной примеси представлены на рис. 8.12. Германий, применяемый в полупроводниковых приборах, обладает удельным сопротивлением от миллионных долей Ом-м до значений, близких к удельному сопротивлению собственного германия

Германий применяется для изготовления диодов различных ти­пов, транзисторов, датчиков ЭДС Холла, тензодатчиков. Оптические свойства германия позволяют его использовать для изготов­ления фотодиодов и фототранзисторов, модуляторов света, опти­ческих фильтров, а также счетчиков ядерных частиц. Рабочий диа­пазон температур германиевых приборов от —60 до +70 °С.

Б) Кремний. В противоположность германию кремний является одним из самых распространенных элементов в земной коре; его со­держание в ней около 29 %. Однако в свободном состоянии в при­роде он не встречается, а имеется только в соединениях в виде окисла и в солях кремниевых кислот. Чистота природной окиси кремния в виде монокристаллов кварца иногда достигает 99,9 %; в ряде мес­торождений чистота песка достигает 99,8—99.9 %.

Технология получения кремния полупроводниковой чистоты вклю­чает в себя следующие операции:

I) превращение технического крем­ния в легколетучее соединение, ко­торое после очистки может быть легко восстановлено; 2) очистка соединения физическими и хими­ческими методами; 3) восстановле­ние соединения с выделением чис­того кремния; 4) конечная очистка кремния методом бестигедьной зонной плавки; 5) выращивание монокристаллов.

В полупроводниковом произ­водстве наибольшее распростране­ние получил метод водородного восстановления трихлорсилана SiHCI₃. Его получают обработкой измельченного технического кремния сухим хлористым водородом при температуре 300 — 400 0 С:

Трихлорсилан представляет собой жидкость с температурой ки­пения 32 0 С. Поэтому он легко очищается методами экстракции, адсорбции и ректификации.

Электропроводность кристаллов SiC при нормальной темпера­туре примесная. Тип электропроводности и окраска кристаллов карбида кремния зависят от инородных примесей или определяются избытком атомов Si или С над стехиометрическим составом. Чистый карбид кремния стехиометрического состава бесцветен. Примеси элементов V группы (N, P, As, Sb, Bi) и железа в карбиде дают зе­леную окраску и электропроводность /г-типа, элементы II (Са, Mg) и III групп (В, Al, Ga, In) — голубую и фиолетовую окраску и электропроводность p-типа. Избыток Si приводит к электронной электропроводности SiC, а избыток С — к дырочной.

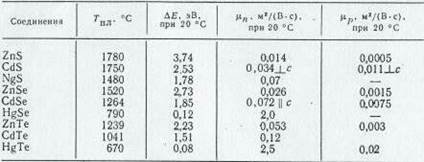
Некоторые параметры рассматриваемых соединений приведены в табл. 8.2.

Арсенид галлия среди соединений A ПI B V занимает особое поло­жение. Большая ширина запрещенной зоны (1,4 эВ). высокая под­вижность электронов [0,85 м 2 /Вс)! позволяют создавать на его основе приборы, работающие при высоких температурах и высоких частотах. Первым полупроводником являлся GaAs, на котором в 1962 г. был создан инжекционный лазер. Он используется для из­готовления светодиодов, туннельных диодов, диодов Гаипа, тран­зисторов, солнечных батарей и других приборов. Для изготовле­ния детекторов в инфракрасной области спектра, датчиков Холла, термоэлектрических генераторов, тензометров применяется анти-монид индия, имеющий очень малую ширину запрещенной зоны (0,17 эВ) и очень высокую подвижность электронов — 7,7 м 2 / (Вс). Широкое применение в серийной производстве светодиодов нашел фосфид галлия, имеющий большую ширину запрещенной, зоны (2,25 эВ). В отличие от других соединений группы A III B V чрезвы­чайно высокой чувствительностью к механическим напряжениям об­ладает антимонид галлия. Удельное сопротивление GaSb увеличи­вается в два раза при воздействии давления 4-10 8 Па. При таком же давлении, приложенном к кристаллам GaAs и 1пР, их удельное со­противление меняется лишь на 3 %. Благодаря высокой чувстви­тельности к деформациям антимонид галлия используют при изго­товлении тензометров.

К полупроводниковым соединениям A II B V I относят халькогениды цинка, кадмия и ртути. Среди них можно выделить сульфиды, селениды и теллуриды.

Основные физические свойства данных соединений указаны в табл. 8.3.

Среди полупроводниковых соединений типа A IV B V I наиболее изученными являются халькогениды свинца: PbS. PbSe, РЬТе. Сульфид, селенид и теллурид свинца в естественном состоянии встре­чаются в виде минералов галенита, клаусталита и алтаита. Первый минерал является одной из самых распространенных руд свинца, два других в природе обнаруживаются довольно редко. Моно­кристаллы PbS, PbSe, РЬТе получают в основном путем осажде­ния из газовой фазы, методом выращивания из расплава или мето­дом медленного охлаждения расплава с использованием естествен­ного градиента температуры печи. Основные физические свойства халькогенидов свинца приведены в табл. 8.4.

Из табл. 8.4 видно, что эти соединения являются узкозонными полупроводниками. Халькогениды свинца используют для изготов­ления фото рези сто ров в инфракрасной технике, инфракрасных лазе­ров, тензометров и термогенераторов, работающих в интервале тем­ператур от комнатной до 600 °С.

Источник