поле внутри заряженной сферы
Электростатическое поле точечного заряда и заряженной сферы
теория по физике 🧲 электростатика
Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.
Электростатическое поле точечного заряда
Направление силовых линий электростатического поля точечного заряда
| Положительный заряд +Q | Отрицательный заряд –Q |
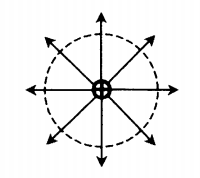 | 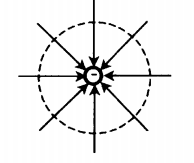 |
| У положительного заряда силовые линии направлены по радиальным линиям от заряда. | У отрицательного заряда силовые линии направлены по радиальным линиям к заряду. |
Модуль напряженности не зависит от значения пробного заряда q0:
Модуль напряженности точечного заряда в вакууме:
Модуль напряженности точечного заряда в среде:
Сила Кулона:
Потенциал не зависит от значения пробного заряда q0:
Потенциал точечного заряда в вакууме:
Потенциал точечного заряда в среде:
Внимание! Знак потенциала зависит только от знака заряда, создающего поле.
Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.
Работа электрического поля по перемещению точечного заряда:
A 12 = ± q ( φ 1 − φ 2 )
Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз? Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:
Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины. Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.
Электростатическое поле заряженной сферы
Направление силовых линий электростатического поля заряженной сферы:
| Положительно заряженная сфера +Q | Отрицательно заряженная сфера –Q |
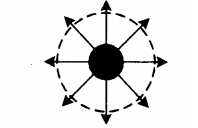 | 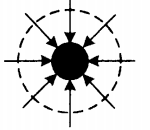 |
| У положительно заряженной сферы силовые линии — это радиальные линии, которые начинаются из этой сферы. | У отрицательно заряженной сферы силовые линии — это радиальные линии, которые заканчиваются в этой сфере. |
Модуль напряженности электростатического поля заряженной сферы:
| Внутри проводника (расстояние меньше радиуса сферы, или r E = 0 a — расстояние от поверхности сферы до изучаемой точки. r — расстояние от центра сферы до изучаемой точки. |
Сила Кулона:
Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.
Так как сфера заряжена положительно, то потенциал тоже положителен:
Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F. Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?
Алгоритм решения
Решение
Запишем исходные данные:
Применим закон Кулона к парам зарядов. Закон Кулона для первой пары:
Закон Кулона для второй пары:
Коэффициент n сократился. Следовательно, силы, с которыми заряды взаимодействуют друг с другом, не изменятся:
После изменения зарядов модуль силы взаимодействия между ними останется равным F.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
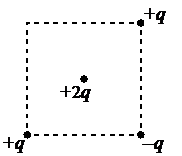
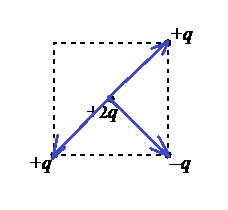
Сделаем чертеж. В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:
Модули всех векторов сил, приложенных к центральному точечному заряду равны, так как модули точечных зарядов, расположенных в вершинах квадрата равны, и находятся они на одинаковом расстоянии от этого заряда.
Складывая векторы геометрически, мы увидим, что силы, с которыми заряд +2q отталкивается от точечных зарядов +q, компенсируют друг друга. Поэтому на заряд действует равнодействующая сила, равная силе, с которой он притягивается к отрицательному точечному заряду –q. Эта сила направлена в ту же сторону (к нижней правой вершине квадрата).
pазбирался: Алиса Никитина | обсудить разбор | оценить
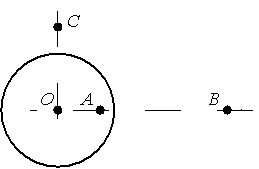
Установите соответствие между физическими величинами и их значениями.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Учебники
Журнал «Квант»
Общие
§9. Электрическое поле и его свойства
9.7. Поле равномерно заряженной сферы
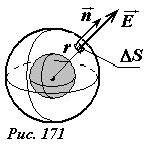
Рассмотрим теперь с помощью теоремы Гаусса, поле, создаваемое равномерно заряженной тонкой сферической оболочки. Опять начнем с рассмотрения симметрии поля. Очевидно, что поле, также как распределение зарядов имеет сферическую симметрию. Это означает, что модуль вектора напряженности зависит только от расстояния до центра сферы (или во всех точках, находящихся от центра сферы на одном расстоянии, модуль напряженности постоянен), а направление — радиальное, от центра сферы к точке наблюдения. Выберем в качестве замкнутой поверхности, к которой применим теорему Гаусса, сферу, концентрическую с заряженной оболочкой (рис. 171).
Пусть радиус сферы r больше радиуса оболочки. Тогда во всех точках этой сферы вектор напряженности направлен вдоль нормали к поверхности, а его модуль постоянен. Поэтому поток вектора напряженности через сферу равен произведению модуля напряженности на площадь сферы \(
Полученная формула, соответствует формуле закона Кулона для точечного заряда, следовательно, вне сферы, поле равномерно заряженной сферы, совпадает с полем точечного заряда, помещенного в центре сферы. Таким образом, результат, на доказательство которого И. Ньютон затратил несколько лет, получен нами почти автоматически. Подчеркнем, что для доказательства формулы (1) помимо теоремы К. Гаусса, потребовалось рассмотреть симметрию поля.
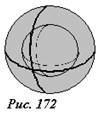
Поле внутри заряженной сферической оболочки также должно обладать сферической симметрией. Поэтому, поток вектора напряженности электрического поля через сферу, концентрическую с заряженной оболочкой и расположенную внутри нее (рис. 172) также выражается формулой \(
Однако внутри этой сферы электрических зарядов нет, поэтому, из теоремы К. Гаусса следует, что напряженность поля внутри сферы равна нулю. Подчеркнем, если бы теорема Гаусса была не справедлива, то внутри равномерно заряженной оболочки существовало бы электрическое поле.
Таким образом, функция, описывающая напряженность поля равномерно заряженной сферы радиуса R, имеет вид (график этой функции показан на рисунке 173)
§ 1.12. Поле заряженной плоскости, сферы и шара
Поле равномерно заряженной бесконечной плоскости
Когда заряд распределен по какой-либо поверхности, то для расчета полей удобно ввести поверхностную плотность заряда с. Выделим на плоской поверхности маленький участок площадью ΔS. Пусть заряд этого участка равен Δq. Поверхностной плотностью заряда называют отношение заряда Δq к площади поверхности, по которой он распределен:
Эта плотность может непрерывно изменяться вдоль поверхности. Конечно, электрический заряд имеет дискретную (прерывную) структуру, так как сосредоточен в элементарных частицах. Но если на поверхности площадью ΔS содержится огромное число элементарных зарядов, то дискретную структуру заряда можно не принимать во внимание. Мы ведь пользуемся понятием плотности, считая, что масса непрерывно распределена в пространстве. А на самом деле все тела состоят из дискретных образований — атомов.
В случае равномерного распределения заряда q по поверхности площадью S поверхностная плотность заряда постоянна и равна:
Рассмотрим бесконечную равномерно заряженную плоскость. Поверхностная плотность заряда σ известна. Из соображений симметрии очевидно, что линии напряженности представляют собой прямые, перпендикулярные плоскости. Поле бесконечной плоскости — однородное поле. Во всех точках пространства, независимо от расстояния до плоскости, напряженность поля одна и та же.
Для применения теоремы Гаусса нужно выбрать замкнутую поверхность таким образом, чтобы можно было легко вычислить поток напряженности электрического поля через эту поверхность. В данном случае удобнее всего выбрать цилиндр, образующие которого параллельны линиям напряженности электрического поля, а основания параллельны плоскости (рис. 1.43).
Тогда поток через боковую поверхность цилиндра будет равен нулю. Поэтому полный поток равен потоку через основания цилиндра А и В:
где Еn — проекция вектора напряженности на нормаль к основанию цилиндра. Полный заряд внутри цилиндра равен σS. Согласно теореме Гаусса
Отсюда модуль напряженности равен:
В СИ эта формула принимает вид:
а в абсолютной системе
Поле равномерно заряженной сферы
Поток напряженности электрического поля через любую замкнутую поверхность внутри сферы равен нулю, так как равен нулю заряд. Это может быть лишь в том случае, когда напряженность поля внутри сферы равна нулю.
Найдем напряженность поля вне сферы. Из соображений симметрии ясно, что линии напряженности начинаются на поверхности сферы (в случае положительного заряда), направлены по радиусам сферы и перпендикулярны ее поверхности (рис. 1.44). Поэтому модуль напряженности поля одинаков во всех точках, лежащих на одинаковых расстояниях от центра сферы.
Проведем сферическую поверхность радиусом r > R, где R — радиус заряженной сферы. Поток напряженности через эту поверхность равен:
Если заряд сферы q, то по теореме Гаусса
Следовательно, модуль напряженности поля при r > R равен:
Таким образом, поле заряженной сферы совпадает вне сферы с полем точечного заряда, расположенного в центре сферы. График зависимости Е(r) изображен на рисунке 1.45.
Поле равномерно заряженного шара
Для характеристики распределения заряда по объему используется понятие объемной плотности заряда. Объемной плотностью заряда называется отношение заряда Δq к объему ΔV, в котором он распределен:
Эта плотность может непрерывно изменяться внутри заряженного тела. Если заряд q равномерно распределен по объему V, то объемная плотность заряда постоянна и равна:
Будем считать, что шар радиусом R равномерно заряжен; плотность заряда ρ известна. Полный заряд шара
Напряженность электрического поля вне шара можно найти с помощью теоремы Гаусса точно так же, как и напряженность равномерно заряженной сферы [см. формулу (1.12.9)]:
(при условии, что r > R). Поле аналогично полю точечного заряда q, расположенного в центре шара.
Для нахождения поля внутри шара нужно применить теорему Гаусса к потоку напряженности через сферическую поверхность радиусом к
Напряженность электрического поля линейно растет с увеличением расстояния вплоть до u = R. При r > R она определяется формулой (1.12.12). График модуля напряженности поля в зависимости от расстояния до центра представлен на рисунке 1.47.
Теорема Гаусса позволяет сравнительно просто определить напряженность электрического поля, если распределение заряда обладает определенной симметрией. Формулы (1.12.5), (1.12.9) и (1.12.15) следует запомнить. Их придется часто использовать.
Вопрос для самопроверки
* Мы предполагаем, что диэлектрическая проницаемость среды одинакова внутри и вне шара.
Поле внутри заряженной сферы
| Вычисление электрических полей с помощью теоремы Остроградского –Гаусса |   |
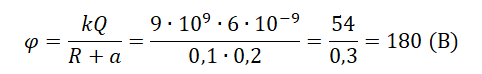




















 во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).


 . Следовательно, из теоремы Остроградского–Гаусса получим:
. Следовательно, из теоремы Остроградского–Гаусса получим:
 .
.


 , то
, то , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
, где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
 для боковой поверхности
для боковой поверхности  т.е. зависит от расстояния r.
т.е. зависит от расстояния r.
 на поверхности будет заряд
на поверхности будет заряд  По теореме Остроградского-Гаусса
По теореме Остроградского-Гаусса  , отсюда
, отсюда
 , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
, т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
 ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при
), то можно вблизи поверхности получить поле с очень большой напряженностью и, при  , получить нить.
, получить нить.

 ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).



 ;
;  – объем шара. Тогда по теореме Остроградского-Гаусса запишем:
– объем шара. Тогда по теореме Остроградского-Гаусса запишем: