поле внутри заряженного цилиндра
Поле внутри заряженного цилиндра
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля 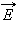
|
Окружим теперь точечный заряд произвольной замкнутой поверхностью и рассмотрим вспомогательную сферу радиуса (рис. 1.3.3).
Таким образом, теорема Гаусса доказана.
Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.
Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.
Этот результат не зависит от радиуса заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).
Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.
Как недопонимание одного явления привело к недопониманию учёными других явлений.
Надеюсь, что в этой попытке написать научно-популярную статью мне удалось докопаться до некоторой истины. Однако, судить вам, читатель.
Электричество — такая же вечная тема для учёных, как и Бог для верующих людей. Только в отличие от Бога, электричество можно ощутить, его действие можно даже увидеть глазами а также с помощью приборов, вследствие этого его можно изучать, его можно подчинить воле человека и, наконец, электрическую энергию можно поставить на службу человеку. Это и было сделано ещё в 19 веке, когда были открыты электромагнетизм, электромагнитная индукция, изобретены электрические трансформаторы, электрические лампы, электрические реле и электрические двигатели, и т.п. Когда в том же 19 веке была открыта возможность генерации радиоволн, а потом и возможность их приёма на некотором удалении от источника, началась новая эра человечества — «Эра Радио».
Итак, чего же, на мой взгляд, изначально недопоняли учёные 19 века, что привело к недопониманию последующими поколениями физиков ряда других явлений и эффектов? Каких именно? Об этом я расскажу в середине своего повествования.
А для начала, вспомним о таком явлении как электростатика.
Электростатика — раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов.
В 1836 году английский учёный Майкл Фарадей заметил, что избыточный заряд на заряженном пустотелом проводнике любой формы локализуется лишь на его внешней стороне и не оказывает никакого влияния на предметы, находящиеся внутри полого проводника.
Из этого следовало, что, если сделать из хорошо проводящей электричество проволоки большую клетку и посадить в неё человека, то даже удары молнии по этой клетке не причинят человеку никакого вреда. Что и демонстрирует практический опыт, представленный на этой фотографии:
К такому убеждению Майкл Фарадей и пришёл в 1836 году, когда он с помощью электроскопа, измеряющего электрический потенциал заряженных тел, смог удостовериться в том, что внутри металлической клетки электрического заряда нет. Если металлическая клетка заряжена статическим электричеством, положительным или отрицательным, весь заряд находится исключительно на наружной стороне металлической клетки.
Почему так?
В электронной энциклопедии сказано: «Принцип работы клетки Фарадея очень простой — при попадании замкнутой электропроводящей оболочки в электрическое поле свободные электроны оболочки начинают двигаться под воздействием этого поля. В результате противоположные стороны клетки приобретают заряды, поле которых компенсирует внешнее поле. » Источник.
На мой взгляд, это неполное объяснение. Оно касается лишь частного случая, когда клетка Фарадея находится вблизи заряженного статическим электричеством некоего тела. Но это не ответ на поставленный вопрос. К тому же, любые тела можно электризовать (заряжать) непосредственно перемещая на них электрические заряды, изъятые из другого заряженного тела.
Поэтому вопрос остаётся открытым: почему избыточный заряд на заряженном пустотелом проводнике любой формы локализуется лишь на его внешней стороне, и почему на внутренней стороне заряженного полого тела заряда нет?
Само это наблюдаемое явление — заряд локализуется на наружной стороне тела — позволило американскому физику Роберту Ван де Граафу создать в 1929 году высоковольтный электрический генератор, названный впоследствии его именем.
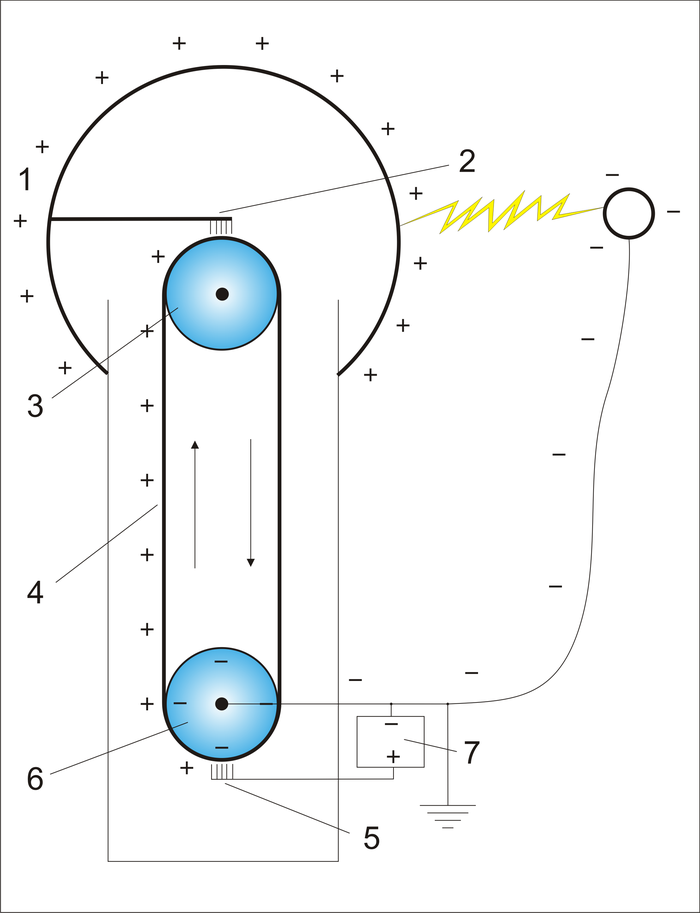
Как работает генератор Ван де Граафа, объясняет приведенная ниже схема: электрические заряды (статическое электричество) порционно вносятся внутрь проводящей сферы с помощью электризуемой кольцевой ленты, движущейся по двум направляющим роликам. Внутри сферы электрические заряды также порционно снимаются с ленты с помощью специальной металлической щётки, и они моментально переходят на наружную сторону проводящей сферы, создавая на ней высокую плотность электрических зарядов, характеризуемую высокой электрической напряжённостью.
«Простой генератор Ван де Граафа состоит из диэлектрической (шёлковой или резиновой) ленты (4 на рисунке), вращающейся на роликах 3 и 6, причём верхний ролик диэлектрический, а нижний металлический и соединён с землёй. Один из концов ленты заключён в металлическую сферу 1. Два электрода 2 и 5 в форме щёток находятся на небольшом расстоянии от ленты сверху и снизу, причём электрод 2 соединён с внутренней поверхностью сферы 1. Через щетку 5 воздух ионизируется от источника высокого напряжения 7, образующиеся положительные ионы под действием силы Кулона движутся к заземлённому 6 ролику и оседают на ленте, движущаяся лента переносит заряд внутрь сферы 1, где он снимается щёткой 2, под действием силы Кулона заряды выталкиваются на поверхность сферы и поле внутри сферы создается только дополнительным зарядом на ленте. Таким образом на внешней поверхности сферы накапливается электрический заряд. Возможность получения высокого напряжения ограничена коронным разрядом, возникающим при ионизации воздуха вокруг сферы.»
Как видите, всё гениальное — просто! А в данном случае до примитива просто!
Первый такой генератор создавал разность электрических потенциалов до 80 тысяч Вольт. А самый мощный генератор Ван де Граафа, созданный в ХХ веке, создавал электрическое напряжение до 7 миллионов Вольт. Источник.
Однако, давайте разбираться, почему избыточный заряд на заряженном пустотелом проводнике любой формы локализуется лишь на его внешней стороне, и почему его нет на внутренней стороне полого тела?
Наука говорит: «В металлах имеется огромное число свободных электронов, которые могут перемещаться по всему объёму металла».
Хорошо, это знание принимается к сведению! Но в нашем случае получается, что избыточные свободные электроны, которые делают тело заряженным, не хотят перемещаться по всему объёму металла, они располагаются только на его наружной поверхности.
В учебниках физики по этому поводу написано: «электрические заряды, сообщённые телу извне, в состоянии равновесия распределяются так, что электрическое поле внутри проводника отсутствует».
Смотрите, опять есть констатация факта, но нет его объяснения, почему? При этом в тех же учебниках сообщается очень важный нюанс: «заряды располагаются в поверхностном тонком слое проводника и характеризуются поверхностной плотностью зарядов».
Если добавить к этому, что заряды противоположного знака притягиваются друг к другу, а заряды одного знака отталкиваются друг от друга, а свободные электроны — это заряды одного знака, то картина более-менее становится понятной.
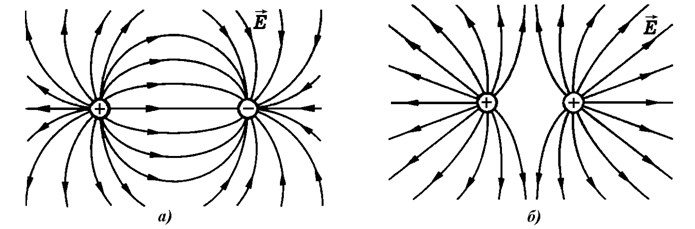
Посмотрите сейчас на рисунок справа, на котором представлено через картину электрических силовых линий взаимодействие двух одноимённых зарядов. Вы видите белое поле между зарядами, свободное от силовых линий? Это нейтральная зона, в которой электрические силы скомпенсированы взаимным противодействием зарядов одного знака!
Возьмём теперь не заряды, а заряженную статическим электричеством прямолинейную проволоку произвольной длины. Если изобразить электрическое поле вокруг неё, то при взгляде с торца прямой проволоки, заряженной положительным или отрицательным электричеством, мы увидим точно такую же картину силовых линий электрического поля, какую создаёт и одиночный точечный заряд.
А если мы теперь свернём проволоку в кольцо и тоже зарядим его статическим электричеством, то картина силовых линий электрического поля вокруг кольца будет примерно такой:
Также эту картину силовых линий электрического поля нетрудно представить объёмной, понимая, что здесь мы рассматриваем кольцо, обращённое к нам боком.
Таким образом, этот рисунок — отличное объяснение, в силу каких причин внутри заряженного проволочного кольца или внутри заряженного проводящего цилиндра, электрическое поле отсутствует.
Что даёт нам это знание?
Сейчас поймёте. Считайте, что это была разминка для ума. Давайте теперь нарисуем в своей голове следующую умозрительную картину:
«В металлах имеется огромное число свободных электронов, которые могут перемещаться по всему объёму металла (это раз), но не могут без особых причин покинуть пределы металла. Если нет проводника свободных электронов, то покидать металл они могут только при коронном разряде, при фотоэффекте или при сильном нагреве металла (это два). Учёные говорят, что счёт свободных электронов в металлах идёт на миллиарды штук на один кубический миллиметр (это три). При этом свободные электроны пребывают в состоянии вечного дистанцирования друг от друга, так как они обладают зарядами одного знака, а зарядам одного знака свойственно отталкиваться друг от друга (это четыре). В силу всего этого под воздействием разных факторов (воздействие стороннего электрического или магнитного поля на металлическое тело или перенос зарядов с тела на тело) свободным электронам свойственно упорядоченно перераспределяться внутри металлических проводников (это пять), с образованием электрического тока (это шесть), но прежде всего им свойственно перераспределяться на наружной поверхности проводников (электростатический «скин-эффект» — это семь), причём это перераспределение происходит с высокой скоростью, величина которой не может превышать скорость распространения в проводниках электрического поля, которая в свою очередь равна скорости света (это восемь).»
Если мы вдумчиво проанализируем эту нашу умозрительную мозаичную картину, состоящую из 8 «пазлов», то мы поймём, что присутствующие во всех металлах в огромных количествах свободные электроны образуют в заряженных телах этакий «электрический флюид» (о существовании которого впервые была высказана догадка ещё в 18 веке, кстати, Бенджамином Франклиным, лик которого изображён на 100 долларовых банкнотах США). Этот «электрический флюид», мало того, что он обладает высокой текучестью, также обладает некоторой плотностью и внутренним давлением. Вот только в отличие от всех жидкостей или газов, он удерживается под давлением (под электрическим напряжением) не внутри электропроводящих тел, а на их наружной поверхности.
Естественной ёмкостью для сбора (накопления) этого вездесущего «электрического флюида» является любая электропроводная поверхность.
В быту мы обычно называем ёмкостью — внутренний объем того или иного сосуда: банки, ведра или канистры, к примеру. Однако, в электротехнике понятие электрическая ёмкость — это характеристика проводника, мера его способности накапливать электрический заряд на своей поверхности.
Таким образом, мы можем представить себе, что все металлические тела представляют собой для электричества «сосуды, вывернутые наизнанку». Их можно наполнять «электрическим флюидом», имеющим свойства текучей жидкости, но собирается эта «электронная жидкость» на наружной поверхности этих сосудов. И вот это свойство всех электропроводных тел накапливать на своей наружной поверхности электрический заряд, и было названо учёными электрической ёмкостью.
Теперь вдумайтесь. С одной стороны, присутствующие во всех металлах в огромных количествах свободные электроны образуют в заряженных телах этакий «электрический флюид», обладающий высокой текучестью, некоторой плотностью и даже массой (ведь каждый отдельно взятый электрон обладает массой 9,10⋅10⁻³¹ кг), с другой стороны, этот «электрический флюид» накапливается на наружной поверхности электропроводных тел.
Но ведь это же как вода, налитая в блюдце до краёв и имеющая открытую поверхность! А на ней, на открытой поверхности, как мы знаем, могут образовываться волны!
Причём волны, которые образуются на поверхности воды, являются поперечными. Поперечная волна – это волна, при распространении которой смещение частиц среды происходит в направлении, перпендикулярном направлению распространения волны.
Вникаем внимательно. Наш «электрический флюид», когда он накапливается на наружной поверхности электропроводных тел, также имеет открытую поверхность (как и вода в океане или вода, налитая в блюдце). А это значит, что на поверхности заряжаемых и перезаряжаемых электропроводных тел (обладающих естественной электрической ёмкостью) в переходные моменты всегда образуются поперечные волны поверхностной плотности зарядов. Причём, как и все упругие волны, они могут быть бегущими, а в некоторых случаях стоячими.
Справка: «Упругие волны — это распространяющиеся возмущения упругой среды. Среда является упругой, если между её частицами существует взаимодействие — возникают силы упругости, препятствующие её деформации. Возмущение упругой среды — это отклонение частиц среды от положения равновесия».
В нашем случае упругая среда, в которой возникают упругие поперечные волны, — это «электрический флюид», находящийся на поверхности заряженных электропроводных тел и состоящий из миллиардов свободных электронов, между которыми действуют силы взаимного отталкивания (Кулоновские силы).
Причём, как я уже сказал, поперечные волны (равно как и продольные волны) могут быть бегущими, а могут быть стоячими.
Бегущие волны образуются всегда при любом возмущении упругой среды. А вот стоячие волны образуются в особом случае – при наложении друг на друга двух встречных бегущих волн с одинаковой длиной и амплитудой. Этот особый случай наступает, например, когда бегущая волна отражается от преграды и движется в противоположную сторону. Тогда падающая на преграду волна превращается в отражённую волну, движущуюся навстречу падающей волне. Вот когда падающая и отражённая волны встречаются и накладываются друг на друга, тогда и образуется стоячая волна.
Продольные волны, которые возникают в толще упругих сред, тоже могут образовывать стоячие волны, когда имеет место отражение бегущих продольных волн от препятствий или от неоднородностей. Об этом я расскажу чуть позже. Продольные волны электрического поля образуются внутри проводов всякий раз, когда по ним протекает переменный электрический ток.
Итак, если мы будем заряжать и перезаряжать прямолинейный незамкнутый проводник (статическим электричеством, например, как в случае с генератором Ван де Граафа), то на его поверхности будут возникать поперечные волны поверхностной плотности электрических зарядов, а в случае цилиндрической формы проводника – поперечно-радиальные волны поверхностной плотности электрических зарядов. При этом в толще проводника будут возникать продольные волны электрического поля. Причём скорость и тех и других волн равна скорости света.
Интересно, не правда ли?
Так вот, поперечные волны поверхностной плотности электрических зарядов, благодаря тому, что они взаимодействуют с открытым пространством, с внешней средой, и порождают в ней радиоволны, уходящие от передающей антенны прочь всё дальше и дальше в открытое пространство со скоростью 300.000 км/с.
В этом и состоит суть работы на излучение так называемого «открытого колебательного контура», отличающегося от «закрытого колебательного контура» тем, что в последнем поперечные волны поверхностной плотности электрических зарядов образуются в закрытом пространстве (в зазоре между пластинами двухполюсного конденсатора.
Я проштудировал многие учебники физики, излучал электродинамику и в конце концов пришёл к выводу, что такую картину излучения радиоволн радиопередающей антенной ещё никто до сих пор почему-то не рассматривал, хотя российские инженеры точно знают о волнах поверхностной плотности электрических зарядов.
Доказательство тому — книга российского физика И.Мисюченко «Последняя тайна Бога», в которой есть такие мысли: «…Если в одном месте проводящей поверхности тем или иным способом нарушить равновесную плотность носителей заряда, то носители придут в движение, стремясь восстановить утраченное равновесие. Поскольку носители инерционны, то процесс восстановления может носить волновой и даже резонансный характер. По всей видимости, Никола Тесла именно этот способ пытался положить в основу не только глобальной всемирной связи, но и энергетики. Поведение подобных поверхностных волн изучено всё ещё плохо. Следует отметить, что поверхностная волна электронной плотности сопровождается и «обычной» электромагнитной волной, и переменным электрическим полем, и специфическими магнитными полями. Такое обилие сопутствующих процессов препятствует объективному изучению явления. »
Вот оно, оказывается как! «Поведение подобных поверхностных волн изучено всё ещё плохо…» При этом теория излучения радиоволн «вибраторами Герца» или «полуволновыми диполями», считается полностью объяснённой шотландским физиком Д.К.Максвеллом (автором «Электромагнитной теории света») и немецким физиком Г.Герцем (первооткрывателем радиоволн).
Так может, всё-таки, механизм излучения радиоволн таки не раскрыт до конца?!
Поле внутри заряженного цилиндра
| Вычисление электрических полей с помощью теоремы Остроградского –Гаусса |   |
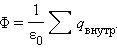



%20(2).gif)


 во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).


 . Следовательно, из теоремы Остроградского–Гаусса получим:
. Следовательно, из теоремы Остроградского–Гаусса получим:
 .
.


 , то
, то , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
, где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
 для боковой поверхности
для боковой поверхности  т.е. зависит от расстояния r.
т.е. зависит от расстояния r.
 на поверхности будет заряд
на поверхности будет заряд  По теореме Остроградского-Гаусса
По теореме Остроградского-Гаусса  , отсюда
, отсюда
 , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
, т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
 ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при
), то можно вблизи поверхности получить поле с очень большой напряженностью и, при  , получить нить.
, получить нить.

 ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).



 ;
;  – объем шара. Тогда по теореме Остроградского-Гаусса запишем:
– объем шара. Тогда по теореме Остроградского-Гаусса запишем: