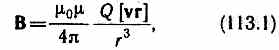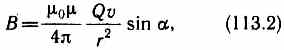поле равномерно движущегося заряда

Поле равномерно двигающегося заряда

При переходе ко второму равенству учтено, что ( γ + 1 ) Γ = γ 2 <\displaystyle \textstyle (\gamma +1)\Gamma =\gamma ^<2>> .

Если бы кулоновская сила в () была регуляризована (стр.\pageref), то в знаменателе дополнительно появилось бы слагаемое + a 2 <\displaystyle \textstyle +a^<2>> .

Обратим внимание, что при выводе () мы использовали постулат инвариантности заряда частицы. Аналогично инвариантности массы, мы считаем, что заряд — это собственная характеристика объекта, не зависящая от его скорости. Другими словами:

где введены электрическое и магнитное поля:

Выражение для напряжённости электрического поля может быть записано следующим образом:

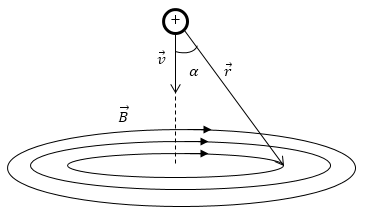
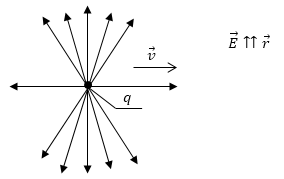
«Густота» линий напряженности символизирует величину поля, поэтому электрическое поле движущегося заряда выглядит примерно так, как изображено на левом рисунке:

где введена функция:

Мы видим, что, несмотря на то, что вектор напряжённости электрического поля не обладает сферической симметрией, дивергенция имеет такое же сингулярное значение, как и в случае неподвижного заряда.

Найдём теперь дивергенцию от магнитного поля:

Используя это соотношение, найдём ротор магнитного поля ():

Аналогично производной электрического поля, производная магнитного поля по времени равна:

Источник

Магнитное поле движущегося заряда

Каждый проводник с током создает в ок­ружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что лю­бой движущийся в вакууме или среде за­ряд создает вокруг себя магнитное поле. В результате обобщения опытных данных

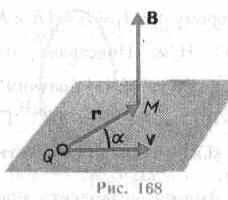
был установлен закон, определяющий по­ле В точечного заряда Q, свободно движу­щегося с нерелятивистской скоростью v. Под свободным движением заряда по­нимается его движение с постоянной ско­ростью. Этот закон выражается формулой

где r — радиус-вектор, проведенный от за­ряда Q к точке наблюдения М (рис. 168). Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и г, а именно: его направление совпадает с на­правлением поступательного движения правого винта при его вращении от v к г. Модуль магнитной индукции (113.1) вычисляется по формуле

где а — угол между векторами v и r.

Сравнивая выражения (110.1) и (113.1), видим, что движущийся заряд по своим магнитным свойствам эквива­лентен элементу тока:

Idl=Qv.

Приведенные закономерности (113.1) и (113.2) справедливы лишь при малых скоростях (v

тельная скорость, т. е. скорость относи­тельно наблюдателя. Вектор В в рассмат­риваемой системе отсчета зависит как от времени, так и от положения точки М на­блюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда.

Впервые поле движущегося заряда удалось обнаружить американскому физи­ку Г. Роуланду (1848—1901). Окончатель­но этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863—1944), изучившим магнит­ное поле конвекционного тока, а также магнитное поле связанных зарядов поля­ризованного диэлектрика. Магнитное поле свободно движущихся зарядов было из­мерено академиком А. Ф. Иоффе, доказав­шим эквивалентность, в смысле возбужде­ния магнитного поля, электронного пучка и тока проводимости.

Источник

Магнитное поле движущегося заряда

Вы будете перенаправлены на Автор24

Модуль вектора индукции поля движущегося заряда

а плотность тока через концентрацию заряженных частиц:

Значит индукция поля, которое создает одна заряженная частица, равна:

Направление вектора индукции поля движущегося заряда

Направление вектора индукции магнитного поля, создаваемого одной частицей перпендикулярно к вектору скорости ($\overrightarrow$) частицы и радиус- вектору ($\overrightarrow$), который проведен из частицы в рассматриваемую точку и подчиняется правилу правого буравчика. Силовыми линиями поля точечного заряда являются концентрические окружности рис.1.

Значит окончательно, вектор магнитной индукции поля, которое создается движущимся зарядом в системе СИ, можно записать как:

Готовые работы на аналогичную тему

Влияние магнитного поля на электрическое поле при движении заряда

Необходимо отметить, что появление в формуле для вектора магнитной индукции вектора скорости означает, что в пространстве появляется выделенное направление. Электрическое поле заряда утрачивает свою сферическую симметрию и становится осесимметричным (рис.2). При скорости движения заряда много меньшей чем скорость света в любой момент времени электрическое поле считается не отличающимся от электростатического поля. Но надо помнить, что поле перемещается вместе с зарядом. Поэтому поле изменяется в каждой точке пространства со временем.

При скоростях сравнимых со скоростью света, поле «сплющивается» в направлении движения и сосредоточено около плоскости, которая перпендикулярна вектору скорости ($\overrightarrow$) (рис.2).

Считаем, что электрон находится в вакууме. За основу решения примем формулу:

Модуль вектора магнитной индукции при этом имеет вид:

Выделим произвольный бесконечно тонкий слой сферы высоты dx. Произвольную площадку поверхности сферы обозначим как dS. Тогда заряд, который находится на такой площадке, равен:

\[dq=dS\cdot \sigma \ \left(2.1\right).\]

Этот заряд, двигаясь вместе с поверхностью сферы, создает магнитное поле в ее центре, которое можно записать как:

Сферу можно разделить на бесконечное количество слоев. Каждый слой создает магнитное поле В, которое рассчитывается по формуле (2.3), для нахождения суммарного поля охарактеризуем положение слоя как:

Источник

Поле равномерно движущегося заряда

О СУЩЕСТВОВАНИИ МАГНИТНОГО ПОЛЯ

Показано, что магнитное поле вокруг цепочки равномерно движущихся зарядов не является суммой магнитных полей отдельных зарядов, а есть результат взаимодействия пробного заряда со всеми зарядами цепочки. Вокруг одиночного движущегося заряда нет никакого магнитного поля. Рассмотрены излучение электромагнитных волн и явление индукции в предположении, что магнитного поля вообще не существует. Указано, что классическая электродинамика может быть построена исходя из формулы для электрического поля произвольно движущегося заряда.

О магнитном поле одиночного движущегося заряда

В середине XIX века Дж. К. Максвелл написал систему уравнений, теоретически обобщившую все известные к тому времени результаты экспериментов с заряженными телами, проводниками с током, магнитными стрелками. Она позволяла с единых позиций объяснить почти все известные к тому времени экспериментальные факты и вводила новое понятие “ток смещения”, в первоначальном варианте только в материальных средах, а затем распространенное Лоренцем и на вакуум.

Проблемы с теорией эфира привели в 1905 г. к появлению теории относительности. На ее основе Leigh Page в 1912 г. [1] сократил количество “сущностей” и объяснил появление магнитных сил, до этого считавшихся проявлением особого «магнитного» поля, через релятивистские эффекты и закон Кулона.

Современные учебники [2,3] приводят вывод магнитных сил, по крайней мере, для параллельных проводников с током. Хотя только в [2] и только качественно рассматривается и случай перпендикулярного движения одиночного заряда к цепочке других движущихся зарядов. Поэтому остановимся на этом вопросе подробнее.

где: e –величина заряда;

R – радиус-вектор от токового заряда до данной точки;

Пересчитав эту силу назад, в лабораторную систему отсчета, нетрудно убедиться, что она равна силе Лоренца действующей со стороны магнитного поля, создаваемого цепочкой токовых зарядов, на пробный заряд или, другими словами, и в данном случае все сводится к закону Кулона и эффектам теории относительности. Собственно говоря, результат этих вычислений можно было предсказать заранее, поскольку величина силы Лоренца не зависит от направления движения пробного заряда.

Более того, поскольку вышеприведенные рассуждения справедливы и в случае притягивающихся частиц и природа сил взаимодействия не играет роли, то аналогичным образом может быть объяснено и гравимагнитное поле, возникающее в общей теории относительности.

Другими словами, магнитное поле вокруг цепочки зарядов не есть сумма магнитных полей отдельных зарядов, а результат взаимодействия пробного заряда со всеми зарядами цепочки образующих ток.

Парадоксы классической электродинамики

С другой стороны, согласно современным представлениям [4], вокруг одиночного движущегося заряда существует движущееся электрическое поле, следовательно, магнитное поле существует и вокруг такого заряда:

Уравнение для rot H :

Для вычисления магнитного поля вдоль контура L нам необходимо проинтегрировать левую и правую части этого уравнения. В соответствии с теоремой Стокса линейный интеграл от вектора H по контуру L будет равен интегралу от rot H по поверхности опирающейся на контур L

Далее. При выводе широко известной формулы Резерфорда для дифференциального сечения рассеяния частиц:

переходят в систему отсчета центра масс обеих сталкивающихся частиц, в которой, неподвижная в лабораторной системе заряженная частица, также движется, и, следовательно, вокруг нее должно существовать магнитное поле. Тем не менее, при выводе формулы рассматривают только кулоновское взаимодействие частиц и получают правильный результат.

О существовании магнитного поля

Пусть мы имеем целую систему зарядов движущихся в произвольных направлениях с различными скоростями и ускорениями и взаимодействующих друг с другом и нас интересует сила, действующая на какой-либо заряд со стороны всех других зарядов. Для вычисления такой силы нам необходимо перейти из лабораторной системы отсчета в систему отсчета связанную с этим зарядом (т. е. в ту, в которой он неподвижен и, следовательно, не участвует в магнитных взаимодействиях). При этом неизбежно изменятся скорости и направления движения всех зарядов входящих в систему. Затем необходимо поочередно вычислить силы электрического взаимодействия между данным зарядом и всеми остальными зарядами системы и векторно сложить их (принцип суперпозиции). Полученная равнодействующая сила будет следствием взаимодействия выбранного нами заряда со всеми остальными в его системе отсчета. При возвращении в исходную, лабораторную систему отсчета, нам придется пересчитать полученную силу в эту систему отсчета. Эта пересчитанная сила в общем случае будет отличаться от исходной как по величине, так и по направлению на некоторый разностный вектор. Это общее правило теории относительности применяемое для всех сил. Однако, в классической электродинамике этот разностный вектор приписывают действию “магнитного поля”.

Все магнитные явления проистекают из того факта, что согласно специальной теории относительности, из разных систем отсчета, движущихся с разными скоростями, окружающий мир представляется по-разному. В разной степени сокращаются длины окружающих предметов, с разной скоростью течет время и что особенно важно в нашем случае, из-за сокращения пространства в направлении движения, меняются плотности зарядов и конфигурации электрических полей. Именно это обстоятельство приводит к появлению магнитных сил. Само по себе изменение электрического поля не приводит к появлению какого-то особого “магнитного поля”.

Если мы объяснили силы, возникающие между проводниками с током и приписываемые действию магнитного поля через закон Кулона и теорию относительности, т. е. доказали что в данном случае никакого особого “магнитного поля” не существует, то непонятно, во что превращается электрическое поле в процессе распространения электромагнитной волны.

В источниках электромагнитных волн, а это, как правило, различные колеблющиеся диполи (мы, оставаясь в рамках классической физики, не рассматриваем излучение атомов и их ядер), в одни моменты времени электрические заряды неподвижны и разнесены на максимально возможное расстояние, затем следует фаза ускоренного движения этих зарядов, пока через четверть периода они не достигнут максимальной скорости и, наконец, торможение зарядов и их остановка. При этом их электрическое поле в заданной точке описывается уравнением [4]:

E = (1)

v – скорость заряда;

R – радиус-вектор между зарядом и точкой наблюдения; ( R – его дли- на)

с – скорость света, e –электрический заряд,

На достаточно больших расстояниях от диполя, за пределами волновой зоны, основную роль играет второе слагаемое, обусловленное ускоренными движениями электрических зарядов. Именно это электрическое поле, распространяясь во все стороны от диполя-излучателя, достигает приемных антенн и приводит в движение электрические заряды в них.

Нет никакой необходимости полагать, что между передающей и приемными антеннами происходит какое-то превращение электрического поля в магнитное и обратно. Иными словами, радиоволны представляют собой просто колебания электрического поля с длиной волны равной расстоянию между максимумами этого поля.

Для малых по сравнению с c скоростей движения заряда формула (1) существенно упростится:

(2)

Конечно, на заряды в верхнем проводнике действует и поле, обусловленное первым слагаемым в формуле (2), однако при вычислении сил действующих на эти заряды со стороны зарядов нижнего проводника, за счет симметрии все усредняется и результирующая сила оказывается направленной поперек верхнего проводника. Более того, поскольку в подавляющем большинстве случаев на практике используются металлические проводники, то поле электронов, обусловленное первым слагаемым, оказывается нейтрализованным зарядом ионного остова металлической решетки.

Хотя при выводе формулы (1) и использованы представления о магнитном поле и его вектор-потенциале, само по себе появление дополнительного электрического поля при ускоренном движении электрических зарядов представляет собой самостоятельный закон природы и только ограниченность наших знаний и зигзаги исторического пути развития науки заставляют привлекать для получения второго слагаемого формулы (1) представления об особом “магнитном” поле.

Другое дело, когда сам провод намотан катушку, уложен в виде “вихря”. В таком случае рассматриваемое электрическое поле, следуя за проводником, так же имеет вид вихря. И именно отсюда появилось представление о вихрях электрического и магнитного полей математически записанных в виде роторов Е и Н и затем распространенное на все электродинамические явления.

Об опытах и теории классиков

Изменение тока в первой катушке также приводит к появлению э. д. с. во второй катушке. Причина этого явления, заключающаяся в электромагнитной индукции, рассмотрена выше.

Основоположники классической электродинамики проводили свои опыты именно с катушками, а поскольку они представляют собою проводники уложенные в виде “вихрей”, то и поля ими создаваемые имели такой же характер. На основании гипотезы Ампера то же самое можно сказать и о магнитных стрелках. Затем представление о вихреобразных полях было ошибочно распространено на все электромагнитные явления. Если предположить, что все электромагнитные явления объясняются законом Кулона, теорией относительности и возникновением дополнительного электрического поля (описываемом вторым слагаемым в формуле (1)) при ускоренном движении зарядов, то все уравнения Максвелла, в которые входят роторы электрического и магнитного полей, должны относиться только к частному случаю полей создаваемых катушками.

Ну а если предположить, что в природе вообще не существует магнитного поля, то теряют физический смысл вообще все уравнения Максвелла в которые оно входит, исчезает необходимость в “токе смещения”. Понятие “ток смещения”, остается в силе только для электрических явлений в материальных средах (в конце концов, в вакууме и смещаться то нечему). Теория Максвелла становится чисто феноменологической теорией, хотя и позволяющей получать практически ценные результаты, но не соответствующей реальному положению вещей. В конце концов, теория движения небесных тел Птолемея так же позволяла кораблям благополучно приходить в порты назначения, хотя и имела мало чего общего с правильной теорией Коперника.

Тем не менее, к настоящему времени на основе теории Максвелла развит мощный математический аппарат, позволяющий получать ценные результаты в электро и радиотехнике и теоретической физике. На ее стороне оказывается и наглядность демонстрации магнитного поля постоянных магнитов и катушек с током. Однако и здесь ситуация похожа на ситуацию с движением небесных тел – нам кажется, что в полном соответствии с теорией Птолемея, все небесные тела обращаются вокруг Земли.

Тем не менее, как и в астрономии, где для многих целей представляется, что небесные тела расположены на вращающейся вокруг Земли бесконечно удаленной небесной сфере, представление о магнитном поле остается очень удобным инструментом при расчете различных устройств, работа которых основана на магнитных явлениях.

Надо сказать, что если считать формулу (1) экспериментально установленным законом природы, то из нее вытекает вся классическая электродинамика. Таблица показывает, как получаются из этой формулы основные ее законы.

Источник

Большая Энциклопедия Нефти и Газа

Равномерно движущийся заряд

Этот метод использует разложение поля в ряд Фурье по пространственным переменным и поэтому не всегда может быть применен в случае диспергирующей среды. Однако поле равномерно движущегося заряда как раз таково, что его пространственные компоненты Фурье гармонически изменяются во времени. [16]

Для практических целей нам нужно найти поля. Равномерно движущиеся заряды попадаются буквально на каждом шагу, скажем проходящие через камеру Вильсона космические лучи или даже медленно движущиеся электроны в проводнике. Так что давайте хотя бы посмотрим, как выглядят эти поля для любых скоростей заряда, даже для скоростей, близких к скорости света, но предположим при этом, что ускорение вообще отсутствует. [19]

Рассмотрим поле излучения ускоренно движущегося квазиточечного заряда. Равномерно движущиеся заряды не излучают. Действительно, для равномерно движущегося заряда существует инерциальная система отсчета, в которой он неподвижен. Излучение же возникает лишь при ускоренном движении заряда. [20]

Следует обратить внимание на тот факт, что на базе ньютоновской механики невозможно объяснить происхождение магнитных сил. В самом деле, в ньютоновской механике силы взаимодействия связаны только с ускорениями. Поэтому согласно ньютоновской механике силы взаимодействия между равномерно движущимися зарядами не должны были бы отличаться от сил взаимодействия между неподвижными зарядами, что не соответствует эксперименту. [22]

Таким образом, заряды могут излучать, только если они движутся с ускорением. Равномерно движущиеся заряды не излучают. Это следует, впрочем, и непосредственно из принципа относительности, так как равномерно движущийся заряд можно рассматривать в такой инерциальной системе, где он покоится, а покоящиеся заряды не излучают. [23]

Таким образом, заряды могут излучать только в случае, если они движутся с ускорением. Равномерно движущиеся заряды не излучают. Это следует, впрочем, и непосредственно из принципа относительности, так как равномерно движущийся заряд можно рассматривать в такой инерциальной системе, где он покоится, а покоящиеся заряды не излучают. [24]

Источник