поле направлений дифференциального уравнения
Метод изоклин для дифференциальных уравнений 1-го порядка
Дифференциальное уравнение первого порядка
Если в каждой точке области задано значение некоторой величины, то говорят, что в области задано поле этой величины. Таким образом, дифференциальное уравнение (1) определяет поле направлений.
Задача интегрирования дифференциального уравнения (1) может быть теперь истолкована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке.
где — параметр. Придавая параметру близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения (1).
Замечание 1. Нулевая изоклина дает уравнение линий, на которых могут находиться точки максимума и минимума интегральных кривых.
Для большей точности построения интегральных кривых находят также геометрическое место точек перегиба. Для этого находят в силу уравнения (1):
и приравнивают ее нулю. Линия, определяемая уравнением
и есть возможное геометрическое место точек перегиба.
Проведенное исследование позволяет нам приближенно построить семейство интегральных кривых уравнения (рис.6).
Интегральные кривые в точках пересечения с этими изоклинами имеют горизонтальные касательные.
Определим, имеют ли интегральные кривые на изоклинах экстремум. Для этого найдем вторую производную:
Для исследования направления вогнутости интегральных кривых найдем вторую производную:
Правая часть исходного уравнения во всех точках плоскости удовлетворяет условиям теоремы существования и единственности, поэтому через каждую точку плоскости проходит единственная интегральная кривая уравнения.
Используя полученные сведения, строим приближенно семейство интегральных кривых данного уравнения (рис. 8).
Замечание 2. Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.
В точке пересекаются все изоклины данного уравнения (особая точка уравнения). С помощью полученных изоклин строим интегральные кривые (рис. 10).
Лекция 1. Понятие дифференциального уравнения
Примеры моделей, приводящих к дифференциальным уравнениям
Рост населения. Мальтузианская модель
Рост экономики. Модель Солоу
Механическая система. Падающий шарик
Если я возьму в руку маленький тяжелый шарик, что с ним произойдёт, когда я его отпущу? Не нужно проводить этот эксперимент на практике и даже решать дифференциальное уравение, чтобы ответить: он станет падать вниз с ускорением. Это подскажет нам наша физическая интуиция. Использование интуиции и ранее накопленного опыта очень важно при решении задач, поэтому мы время от времени будем обращаться к механическим примерам.
Простейшие дифференциальные уравнения
Дифференциальное уравнение общего вида
Рассмотрим несколько примеров.
Нулевая правая часть
Постоянная правая часть
Заметим, что в этом случае \( C \) задаёт значение функции в начальный момент времени \( t=0 \).
Правая часть, зависящая только от времени
Неопределенный интеграл по определению является семейством функций, а при записи его в виде определенного интеграла с переменным верхним пределом нужно указывать константу интегрирования явным образом.
Начальные условия. Задача Коши
Чтобы выделить среди семейства решений дифференциального уравнения одно, обычно вместе с самим дифференциальным уравнением рассматривают дополнительное соотношение, называемое начальным условием — значение решение в какой-то момент времени (не обязательно \( t=0 \)).
Когда задано дифференциальное уравнение и начальное условие, говорят, что поставлена задача Коши.
Поле направлений
Смотреть что такое «Поле направлений» в других словарях:
Поле направлений — (штрихи) и изоклины Поле направлений геометрическая интерпретация множества линейных элементов, соответствующих системе обыкновенных дифференциальных уравнений … Википедия
Поле (в сельском хоз-ве) — Поле, 1) обширное, ровное, безлесное пространство. 2) В сельском хозяйстве участки пашни, на которые разделены площадь севооборота, а также внесевооборотные (запольные) участки, используемые для выращивания с. х. растений. 3) Ограниченный… … Большая советская энциклопедия
Поле — I Поле 1) обширное, ровное, безлесное пространство. 2) В сельском хозяйстве участки пашни, на которые разделены площадь Севооборота, а также внесевооборотные (запольные) участки, используемые для выращивания с. х. растений. 3)… … Большая советская энциклопедия
поле допуска перпендикулярности оси (или прямой) относительно плоскости — 1) область в пространстве, ограниченная цилиндром, диаметр которого равен допуску перпендикулярности TPR, а ось перпендикулярна к базовой плоскости; 2) область в пространстве, ограниченная прямоугольным параллелепипедом, стороны сечения которого… … Справочник технического переводчика
поле допуска прямолинейности оси (или линии) в пространстве — 1) область в пространстве, ограниченная цилиндром, диаметр которого равен допуску прямолинейности TFL; 2) область в пространстве, ограниченная прямоугольным параллелепипедом, стороны сечения которого равны допускам прямолинейности оси (линии) в… … Справочник технического переводчика
поле позиционного допуска оси (или прямой) в пространстве — 1) Область в пространстве, ограниченная цилиндром, диаметр которого равен позиционному допуску в диаметральном выражении TPP или удвоенному позиционному допуску в радиусном выражении R, а ось совпадает с номинальным расположением рассматриваемой… … Справочник технического переводчика
Лодейное Поле — Город Лодейное Поле Флаг Герб … Википедия
АТ-поле (Евангелион) — Это глоссарий терминов не вошедших в базовые статьи о линейке аниме и манги Neon Genesis Evangelion. Содержание 1 Снаряжение 1.1 AT Поле 1.2 LCL 1.3 … Википедия
АТ-поле — Это глоссарий терминов не вошедших в базовые статьи о линейке аниме и манги Neon Genesis Evangelion. Содержание 1 Снаряжение 1.1 AT Поле 1.2 LCL 1.3 … Википедия
Поле направлений дифференциального уравнения
уЙНЧПМЙЮЕУЛЙ ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ НПЦОП ОБРЙУБФШ ФБЛ
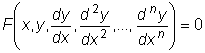
рПТСДЛПН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС ОБЪЩЧБЕФУС РПТСДПЛ ОБЙЧЩУЫЕК РТПЙЪЧПДОПК, ЧИПДСЭЕК Ч ХТБЧОЕОЙЕ.
оБРТЙНЕТ, ХТБЧОЕОЙЕ
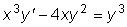
ЕУФШ ХТБЧОЕОЙЕ РЕТЧПЗП РПТСДЛБ, Б ХТБЧОЕОЙЕ
— ХТБЧОЕОЙЕ ЧФПТПЗП РПТСДЛБ.
тЕЫЕОЙЕН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС ОБЪЩЧБЕФУС ЧУСЛБС ЖХОЛГЙС y(x), ЛПФПТБС ВХДХЮЙ РПДУФБЧМЕООПК Ч ХТБЧОЕОЙЕ, ПВТБЭБЕФ ЕЗП Ч ФПЦДЕУФЧП. тЕЫЕОЙЕ ЕЭЕ ОБЪЩЧБЕФУС ЙОФЕЗТБМПН ДЙЖЖЕТЕОГЙБМШОПЗП ХТБЧОЕОЙС.
рТЙНЕТ
тБУУНПФТЙН ХТБЧОЕОЙЕ 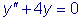
жХОЛГЙС 
дЕКУФЧЙФЕМШОП,
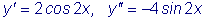
Й ХТБЧОЕОЙЕ ПВТБЭБЕФУС Ч ФПЦДЕУФЧП: 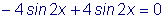
тЕЫЕОЙЕН ТБУУНБФТЙЧБЕНПЗП ХТБЧОЕОЙС ВХДХФ Й ЖХОЛГЙЙ
Й ЧППВЭЕ ЖХОЛГЙЙ 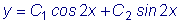

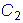
ч УБНПН ДЕМЕ
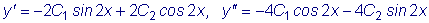
Й ХТБЧОЕОЙЕ ПВТБЭБЕФУС Ч ФПЦДЕУФЧП 
ъБНЕФЙН, ЮФП ТБУУНБФТЙЧБЕНПЕ ХТБЧОЕОЙЕ ЙНЕЕФ ВЕУЮЙУМЕООПЕ НОПЦЕУФЧП ТЕЫЕОЙК ЧЙДБ: 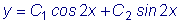
тЕЫЕОЙЕ ДЙЖЖЕТЕОГЙБМШОЩИ ХТБЧОЕОЙК РЕТЧПЗП РПТСДЛБ
дЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ РЕТЧПЗП РПТСДЛБ ЙНЕЕФ ЧЙД 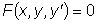
пВЭЕЕ Й ЮБУФОПЕ ТЕЫЕОЙЕ
рТЙНЕТ
тБУУНПФТЙН ХТБЧОЕОЙЕ
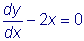
пВЭЙН ТЕЫЕОЙЕН ЬФПЗП ХТБЧОЕОЙС СЧМСЕФУС УЕНЕКУФЧП ЖХОЛГЙК
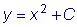
дЕКУФЧЙФЕМШОП, РТЙ МАВПН ЪОБЮЕОЙЙ C ЬФБ ЖХОЛГЙС ХДПЧМЕФЧПТСЕФ ХТБЧОЕОЙА: 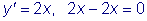
лТПНЕ ФПЗП, ЧУЕЗДБ НПЦОП ОБКФЙ ФБЛПЕ ЪОБЮЕОЙЕ C, ЮФП УППФЧЕФУФЧХАЭЕЕ ЮБУФОПЕ ТЕЫЕОЙЕ ВХДЕФ ХДПЧМЕФЧПТСФШ ЪБДБООПНХ ОБЮБМШОПНХ ХУМПЧЙА.
ьФП ТЕЫЕОЙЕ НПЦОП РПМХЮЙФШ, ЙУРПМШЪХС ОЙЦЕРТЙЧЕДЕООЩК БРРМЕФ ДМС РПУФТПЕОЙС РПМС ОБРТБЧМЕОЙК Й ЙОФЕЗТБМШОЩИ ЛТЙЧЩИ ДМС ХТБЧОЕОЙС РЕТЧПЗП РПТСДЛБ.
тЕЫЙФШ ЙМЙ РТПЙОФЕЗТЙТПЧБФШ ДБООПЕ ДЙЖЖЕТЕОГЙБМШОПЕ ХТБЧОЕОЙЕ ЬФП ЪОБЮЙФ:
Б) ОБКФЙ ЕЗП ПВЭЕЕ ТЕЫЕОЙЕ ЙМЙ ПВЭЙК ЙОФЕЗТБМ, ЕУМЙ ОЕ ЪБДБОЩ ОБЮБМШОЩЕ ХУМПЧЙС,
В) ОБКФЙ ЮБУФОПЕ ТЕЫЕОЙЕ, ХДПЧМЕФЧПТСАЭЕЕ ЪБДБООЩН ОБЮБМШОЩН ХУМПЧЙСН.
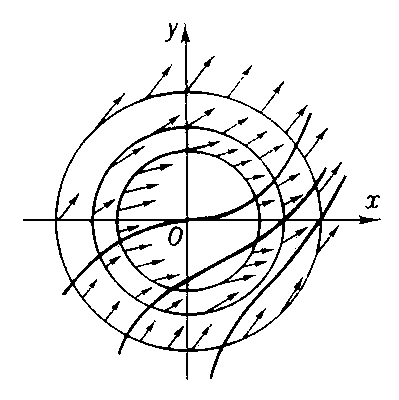
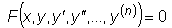


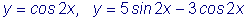


 (1) Линейным элементом наз. набор чисел
(1) Линейным элементом наз. набор чисел  (2) где
(2) где  — точка области
— точка области  , в к-рой определены правые части системы (1). Линейный элемент (2) можно представить себе как совокупность точки
, в к-рой определены правые части системы (1). Линейный элемент (2) можно представить себе как совокупность точки  и соответствующего ей направления с направляющими косинусами
и соответствующего ей направления с направляющими косинусами


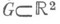 правой части уравнения 1-го порядка
правой части уравнения 1-го порядка 


 для точек
для точек  в к-рых
в к-рых 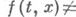
 , и
, и  для точек
для точек  , в к-рых функцию
, в к-рых функцию  можно доопределить этим значением по непрерывности. Тем самым для пары уравнений (4), (5) область Gрасширяется до области Go за счет пополнения точками, в к-рых направление параллельно оси х, а интегральным кривым разрешается иметь и точки с вертикальной касательной.
можно доопределить этим значением по непрерывности. Тем самым для пары уравнений (4), (5) область Gрасширяется до области Go за счет пополнения точками, в к-рых направление параллельно оси х, а интегральным кривым разрешается иметь и точки с вертикальной касательной.