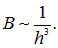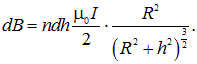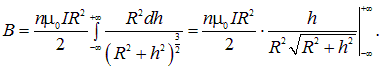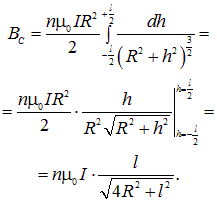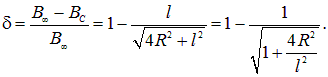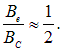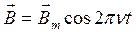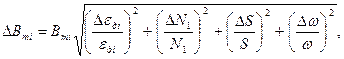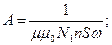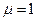поле на оси соленоида
6.4. Магнитное поле соленоида
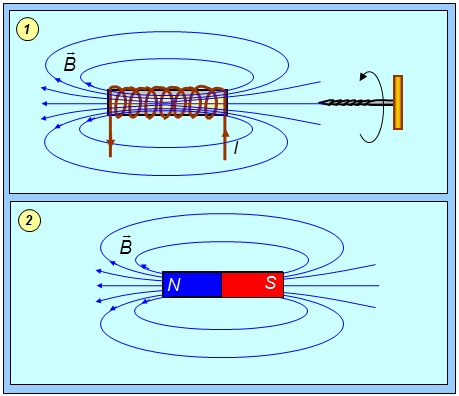
Соленоидом называется цилиндрическая катушка, состоящая из большого числа витков провода, образующих винтовую линию (рис. 6.23-1).
Рис. 6.23. Магнитные силовые линии поля: 1 — соленоида; 2 — полосового магнита
Магнитное поле соленоида напоминает поле полосового магнита (рис. 6.23-2).
Если витки намотаны вплотную, то соленоид — это система круговых токов, имеющих одну ось.
Если считать соленоид достаточно длинным, то магнитное поле внутри соленоида однородно и направлено параллельно оси. Вне соленоида вдали от краев магнитное поле также должно иметь направление параллельное оси и на большом расстоянии от соленоида должно быть очень слабым. Поле убывает по закону
Подсчитаем поле внутри соленоида. Возьмем элемент соленоида длиной dh, находящийся на расстоянии h от точки наблюдения. Если катушка имеет n витков на единицу длины, то в выделенном элементе содержится ndh витков. Согласно формуле (6.11), этот элемент создает магнитное поле
Интегрируя по всей длине соленоида, получаем
Таким образом, поле в бесконечно длинном соленоиде дается выражением
На практике соленоиды бесконечно длинными не бывают. Для иллюстрации рассмотрим некоторые примеры.
Пример 1. Найти магнитное поле в середине соленоида конечной длины l (рис. 6.24). Сравнить с полем бесконечно длинного соленоида. При каких условиях разница составляет менее 0,5 %?
Рис. 6.24. Магнитное поле катушки конечной длины
В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки
Решение. Магнитное поле в средней точке оси соленоида конечной длины l дается тем же интегралом (6.19), но с другими пределами интегрирования
Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна
По условию эта разница мала: 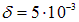
Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.
Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.
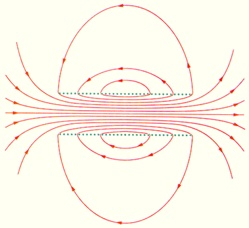
На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.
Рис. 6.25. Визуализация силовых линий магнитного поля
Видео 6.1. Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.
Поле на оси соленоида
Применим теорему о циркуляции вектора 

Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.
Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричные относительно такой плоскости витки создают поле, в котором вектор 
Из параллельности вектора 
Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.
Второй и четвёртый интегралы равны нулю, т.к. вектор 

Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда
где 

Если отрезок 1–2 внутри соленоида, контур охватывает ток:
где n – число витков на единицу длины, I – ток в соленоиде (в проводнике).
Тогда магнитная индукция внутри соленоида:
 , , | (2.7.1) |



Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри.
Произведение nI – называется число ампер витков на метр.
У конца полубесконечного соленоида, на его оси магнитная индукция равна:
 , , | (2.7.2) |
Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца.
Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем:
· В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:
 , , | (2.7.3) |
где L – длина соленоида, R – радиус витков.
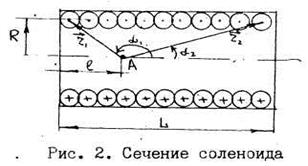
· В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле
 , , | (2.7.4) |
На рисунке 2.15 изображены силовые линии магнитного поля 
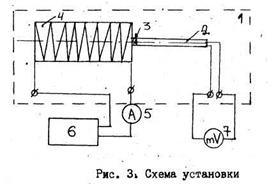
ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА



Приборы и принадлежности: лабораторная установка с соленоидом, источник питания, милливольтметр, амперметр.
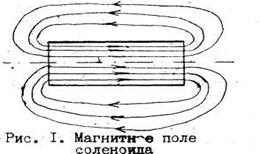
Магнитное поле внутри соленоида можно представить как сумму магнитных полей, создаваемых каждым витком. Вектор индукции магнитного поля внутри соленоида перпендикулярен плоскости витков, т.е. направлен по оси соленоида и образует с направлением кольцевых токов витков правовинтовую систему. Примерная картина силовых линий магнитного поля соленоида показана на рис. 1. Силовые линии магнитного поля замкнуты.
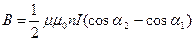
где 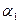
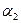
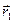
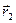
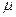
Таким образом, магнитная индукция В прямо пропорциональна силе тока, магнитной проницаемости среды, заполняющей соленоид, и числу витков на единицу длины. Магнитная индукция также зависит от положения точки А относительно концов соленоида. Рассмотрим несколько частных случаев:
1. Пусть точка А находится в центре соленоида, тогда 
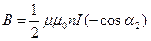
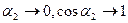
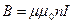
2. Пусть точка A находится в центре крайнего витка, тогда 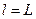
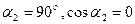
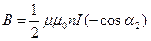
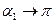
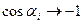
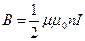
Из формул (2) и (3) видно, что магнитная индукция соленоида на его краю вдвое меньше по сравнению с ее величиной в центре.
3. Если длина соленоида во много раз больше радиуса его витков
(«бесконечно» длинный соленоид), то для всех точек, лежащих внутри
соленоида на его оси, можно положить 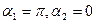
поле можно считать в центральной части соленоида однородным и рассчитывать его по формуле
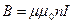
Однородность магнитного поля нарушается вблизи краев соленоида. В этом случае индукцию можно определять по формуле
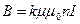
Амплитуда магнитной индукции 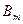
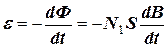
Так как величина индукции B изменяется по закону 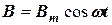
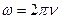
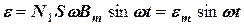
Из выражения (7) видно, что амплитуда ЭДС 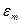
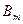
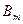
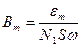
Коэффициент k учитывающий неоднородность магнитного поля соленоида на краях, можно о определить., по формуле. (5), зная 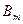
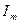
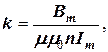
где 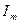
Из формул (7) и (9) следует, что амплитуда ЭДС индукции прямо пропорциональна амплитуде переменного тока 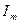
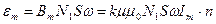
Включенные в цепь переменного тока амперметр и милливольтметр измеряют действующие значения тока 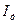
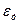
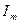
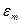
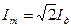
Для действующих значений тока и ЭДС формула (10) имеет вид
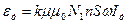
Из формулы (11) следует, что отношение 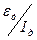
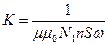
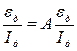
В данной работе требуется выполнить два задания: 1) определить распределение индукции вдоль оси соленоида при некотором постоянном значении тока; 2) определить значение коэффициента к.
1. Не подключают/ самостоятельно источник питания и милливольтметр к сети 220 В.
2. Не производить переключения цепей, находящихся под напряжением.
Не прикасаться к неизолированным частям цепей.
3. Не оставлять без присмотра включенную схему.
Порядок выполнения работы
Задание № 1. Исследование распределения индукции магнитного поля вдоль оси соленоида.
3- соленоид
5- амперметр
6- источник питания с регулятором выходного напряжения (тока), 7- милливольтметр.
2. Установить шток с масштабной линейкой так, чтобы катушка-зонд оказалась примерно в середине соленоида.
3.Включить источник питания соленоида и установить ток соленоида (по амперметру), равный 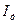
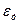
4.Перемещая шток с масштабной линейной, измерить при помощи
милливольтметра действующее значение ЭДС индукции через каждый
сантиметр положения линейки. По формуле (8) вычислить 
Результаты измерений и расчетов занести в таблицу 1 (учтите, что 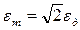
| № п/п | Положение линейки-Х | 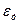 | 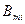 | 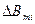 |
| … |
Погрешность 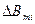
5.Построить график
6.Зная амплитуду тока 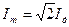
длины соленоида n, определить 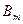
формуле (4) и сравнить с измеренным в той же точке значением
Задание 2. Измерение коэффициента неоднородности’ магнитного
поля соленоида.
1. Снять зависимость 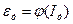
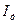
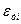
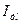
| Измерения | 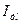 | 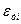 | 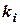 | 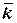 | 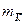 |
| … |
По формуле (12) рассчитать 
1. 

2. Нарисуйте картину силовых линий соленоида.
3. Перечислите основные способы исследования магнитного поля.
4. В каких случаях для исследования магнитного поля можно использовать катушку-зонд?
5. Выведите формулу для вектора магнитной индукции бесконечно длинного соленоида.
Литература
3. Скорохватов Н.А. Курс лекций по электромагнетизму. М: МИИГАиК, 2006.
4. Савельев И.В., Курс общей физики, т. 2 (любое издание).
5. Трофимова Т.И., Курс физики (любое издание).