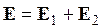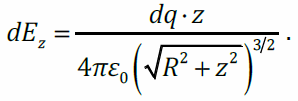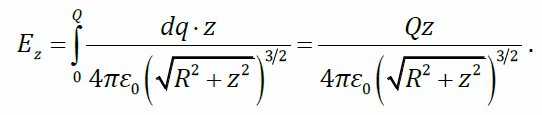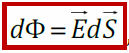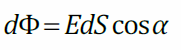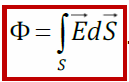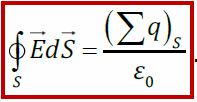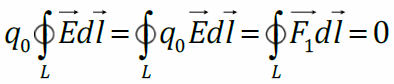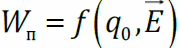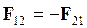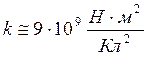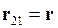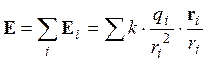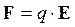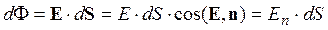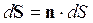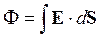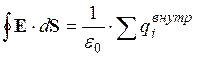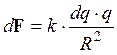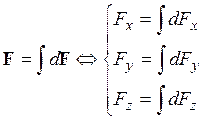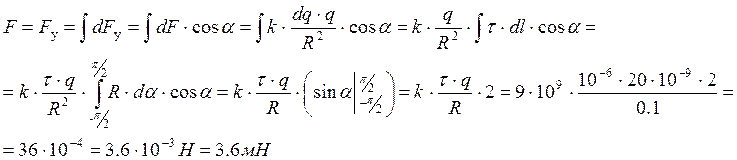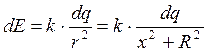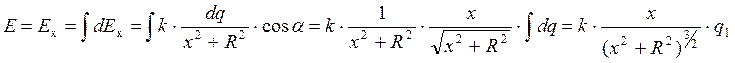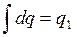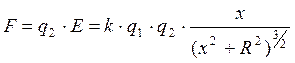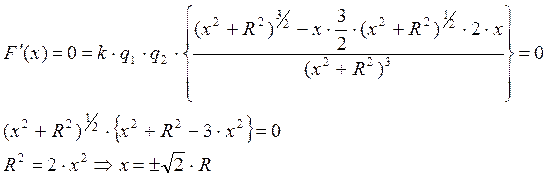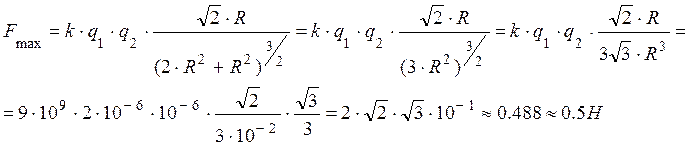поле на оси кольца

Напряженность кольца

Рассмотрим кольцо радиусом R, равномерно заряженное с линейной плотностью . Найдем напряженность поля в точке, расположенной на оси кольца на расстоянии h от его центра.
Напряженность поля элементарного заряда равна . При интегрировании необходимо учесть осевую симметрию, которая приводит к равенству нулю интеграла . Из рисунка видно, что , а , тогда .
Чтобы найти напряженность поля в центре кольца положим h = 0, тогда напряженность в центре кольца равна нулю.

Страница обновлена: 05.02.2018

Отзывы и пожелания можно направлять по адресу energ2010@yandex.ru

Информация предоставлена для ознакомления и не является официальным источником.

Источник

Пример расчета напряженности Электрического поля равномерно заряженного тонкого кольца

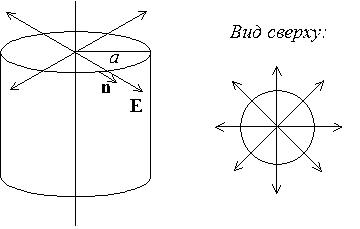
Векторы напряжённости электрического поля каждого из этих зарядов одинаковы по модулю и направлены так, что концы этих векторов образуют конус с вершиной в точке A (штриховой линией показано основание этого конуса). Проекции этих векторов на плоскость кольца компенсируются, поэтому суммарный вектор направлен вдоль оси z: E (при z > 0). Вычислим Ez. Напряжённость поля точечного заряда:

Величины r иθ (угол) одинаковы для всех элементов dq:

подставим

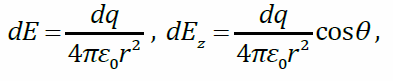
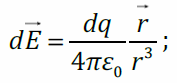
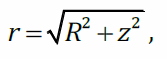
В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:

Поток вектора напряженности. Теорема Остроградского-Гауса для электростатического поля в вакууме. Применение теоремы к расчету напряженности поля. Пример: поле бесконечно большой равномерно заряженной плоскости.

Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля(Φ).

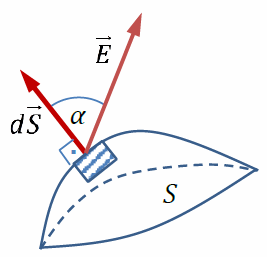
Элементарный поток направлен по внешней нормали к малому участку dS (Если поверхность S не замкнута, то выбор одного из двух направлений нормали произволен, при этом направление нормали для всех участков dSдолжно быть одинаковым)

Полный поток вектора сквозь поверхность S E

Теорема Остроградского-Гаусса для :поток вектора напряжённости электрического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченной этой поверхностью, делённой на ε0:

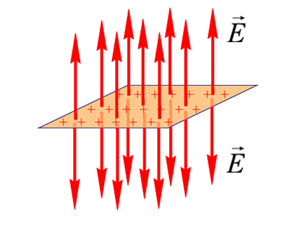
Поле равномерно заряженной бесконечной плоскости:
, где — поверхностная плотность заряда.

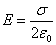
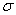
Работа сил электростатического поля по перемещению заряда. Потенциал электростатического поля. Связь между напряженностью поля и потенциалом. Понятие градиента. Методы расчета потенциала. Пример: потенциал на оси равномерно заряженного кольца.

I уравнение Максвелла для электростатического поля умножим на пробный заряд q0:

Работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатическое поле потенциально. Потенциальная энергиязаряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении: .Потенциальная энергия – характеристика и поля, и заряда:

Потенциалом электростатического поля [φ] = В (вольт) называется физическая величина, равная отношению потенциальной энергии заряда q₀ в данной точке пространства, к величине этого заряда.

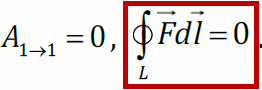
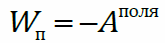
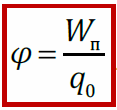
Разность потенциалов – это работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.

Дата добавления: 2016-07-05 ; просмотров: 13142 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Поле на оси кольца

В XIX веке английский учёный Майкл Фарадей выдвинул гипотезу, что электрическое и магнитное взаимодействия осуществляются посредством особой среды между ними, поля. Любой заряд `q` изменяет свойства пространства вокруг себя – создаёт вокруг себя поле, а уже это поле действует на другие заряды. Развитие науки и техники показало чрезвычайную плодотворность концепции поля. Вся теория электромагнитных явлений со всеми её приложениями существенным образом основывается на концепции поля. По мнению Эйнштейна, идея поля была самым важным открытием со времён Ньютона.

Идея электрического поля большинству людей кажется некоей абстрактной теоретической концепцией, поскольку электрическое поле (в отличие от поля магнитов) в обыденной жизни, в быту невозможно «почувствовать рукой». К вопросу о том, почему это так, мы вернёмся позже. Пока же обратимся к количественному описанию электростатического поля.

Если в поле точечного заряда `q` поместить на расстоянии `r` пробный точечный заряд `q_1`, то на этот заряд будет действовать сила `|vecF_1|=1/(4pi epsilon_0) (|q||q_1|)/(r^2)`. Если в ту же точку поместить другой пробный заряд `q_2`, то на него заряд со стороны заряда `q` будет действовать другая сила `|vecF_2|=1/(4pi epsilon_0) (|q||q_2|)/(r^2)`. Существенно, однако, что отношение силы, действующей на пробный заряд, к его заряду, `(vecF_1)/(q_1)=(vecF_2)/(q_2)`, останется одним и тем же и будет характеристикой не пробных зарядов, но исходного заряда `q` и местоположения `vecr` точки `A`, в которую мы помещали пробные заряды (см. рис. 1). Эта характеристика называется напряжённостью электрического поля точечного заряда `q` в точке `A`. Напряжённость поля есть векторная величина. Её модуль равен

`|vecE|=1/(4pi epsilon_0) (|q|)/(r^2)`. (1.3.1)

Если заряд `q` положительный, то вектор `vecE` в точке `A` направлен в сторону от заряда вдоль прямой, соединяющей точечный заряд `q` и точку `A`; если же заряд `q` отрицательный, то вектор `vecE` в точке `A` направлен в сторону к заряду вдоль той же прямой.

`vecE=1/(4pi epsilon_0) q/(r^2) vece`. (1.3.1′)

Формулу (1.3.1.) иногда записывают в виде `|vecE|=1/(4pi epsilon_0) (|q|*(+1))/(r^2)`; при этом о напряжённости говорят как о силе, действующей со стороны заряда `q` на некий условный единичный положительный точечный заряд `(+1)` (не заряд в `+1` Кл!). Нужно, впрочем, помнить, что сила и напряжённость электрического поля имеют разную размерность. В системе СИ напряжённость электрического поля измеряется в вольтах на метр (В/м): `1`В/м `=1`Н/`1`Кл.

Принцип суперпозиции. Напряжённость есть векторная величина. Это означает, что если имеются два заряда `q_1` и `q_2` каждый из них в некоторой точке создаёт свои напряжённости поля `vecE_1` и `vecE_2`, то результирующая напряжённость (результирующая сила, действующая на единичный положительный заряд, со стороны обоих зарядов) будет равна векторной сумме

получаемой по правилу параллелограмма (рис. 2) или треугольника.

Аналогично, в случае `N` зарядов:

`vecE=vecE_1+vecE_2+. +vecE_N=sum_(k=1)^N vecE_k`, (1.3.3)

причём векторная сумма вычисляется по правилу многоугольника (либо последовательно несколько раз по правилу параллелограмма).

Введя понятие напряжённости электрического поля, мы каждой точке пространства около заряда `q` (или около системы зарядов) приписываем некоторый вектор `vecE=1/(4pi epsilon_0) q/(r^2)vece` (в случае системы зарядов нужно ещё вычислить сумму (1.3.3.)), который, в конце концов, позволяет вычислять по формуле `vecF=q^’vecE` силу, действующую на любой другой заряд `q^’`.

Расстояние между точечными зарядами `q_1=+1` нКл и `q_2=-2` нКл равно `d=13` см. Определить напряжённость результирующего электрического поля обоих зарядов в точке, расположенной на расстоянии `r_1=5` см от первого и `r_2=12` см от второго заряда.

Легко заметить, что `r_1^2+r_2^2=d^2`, т. е. треугольник, образованный зарядами и интересующей нас точкой, прямоугольный. Поэтому напряжённости, создаваемые в этой точке отдельными зарядами, перпендикулярны друг другу (рис. 3). Далее, по теореме Пифагора

`E=sqrt(E_1^2+E_2^2)`, где `E_1=1/(4pi epsilon_0) (q_1)/(r_1^2)=3600` В/м и `E_2=1/(4pi epsilon_0) (|q_2|)/(r_2^2)=1250` В/м.

Электрическое поле равномерно заряженной сферы. Вне равномерно заряженной сферы электрическое поле точно такое же, какое создавал бы помещённый в центр сферы точечный заряд, равный по величине суммарному заряду сферы (рис. 4, а – б). Нетривиальный факт состоит в том, что внутри равномерно заряженной сферы напряжённость электрического поля равна нулю (см. `[2 – 3]`).

Если имеются две концентрические равномерно заряженные сферы, то за пределами обеих сфер поле такое же, какое создавали бы два точечных заряда, равные зарядам сфер и помещённые в их общий центр. В области между сферами внешняя сфера не вносит вклада в напряжённость поля.

Вне равномерно заряженного по объёму шара электрическое поле точно такое же, какое создавал бы помещённый в центр шара точечный заряд, равный по величине суммарному заряду шара. Последнее легко понять: поле шара можно представить как результирующее поле множества тонких шаровых слоёв («сфер»). О том, каким будет поле внутри шара, см. Пример 8.

Оценить заряд Земли `Q`, если известно, что в среднем вблизи поверхности Земли существует статическое электрическое поле, направленное вниз перпендикулярно поверхности Земли в каждой её точке, напряжённость которого равна `E

130` В/м. Радиус Земли `R

Напряжённость электрического поля направлена вниз перпендикулярно поверхности Земли, т. е., к центру Земли. Отсюда можно сделать вывод, что заряд Земли отрицателен. По формуле (1.3.1).

Хотя атмосфера Земли обладает положительным электрическим зарядом, она не вносит вклада в напряжённость электрического поля на поверхности Земли (каждый из её сферических слоёв даёт нулевой вклад в напряжённость поля). Напряжённость поля порядка `130` В/м есть среднее поле вблизи поверхности Земли. При приближении, например, грозовой тучи поле может возрасти в тысячи раз.

Какой максимальный заряд можно сообщить металлическому шарику радиусом `r=1` см, чтобы ещё не происходило пробоя воздуха. Пробойное поле сухого воздуха `E_»пр»

3*10^6` В/м. (Если напряжённость электрического поля больше этого значения, происходит пробой воздуха – воздух начинает проводить электричество (возникает электрический ток) – и заряд стекает с заряженных тел на другие тела.)

По формуле (1.3.1) получаем `q_(max)=4pi epsilon_0E_»пр»r^2

Оценить силу взаимодействия двух шариков радиусом `r=1` см, заряженных до максимально возможного заряда (чтобы ещё не происходило пробоя воздуха вблизи шариков) при расстоянии между центрами шариков `d=10` см. Пробойное поле сухого воздуха `E_»пр»

`f=1/(4pi epsilon_0) (q_(max)^2)/(d^2)=1/(4pi epsilon_0) ((4pi epsilon_0E_»пр»r^2)^2)/(d^2)=(4pi epsilon_0E_»пр»^2r^4)/(d^2)

Мы получили весьма малую силу (сила тяжести, действующая на льдинку массой `1` г объёмом примерно в `1 «см»^3`, почти в `10` раз больше). Вот почему, хотя электрические силы обычно считаются большими, заметить их не всегда легко. Реально мы видим лишь электрическое притяжение друг к другу очень лёгких тел (например, листочков бумаги к наэлектризованной расчёске).

Пользуясь тем свойством, что внутри равномерно заряженной сферы напряжённость электрического поля равна нулю, найти напряжённость поля внутри равномерно по объёму заряженного шара радиусом `R` и зарядом `Q`. (К таким практически равномерно по объёму заряженным шарам можно с хорошей точностью отнести, например, атомные ядра.)

Электрический диполь. Так называется система, состоящая из двух точечных зарядов равных по величине, но противоположных по знаку. Пусть заряды `q_1=-q` и `q_2=+q` в некоторой системе координат характеризуются радиус-векторами `vecr_1` и `vecr_2` (см. рис. 6). Дипольным моментом диполя называется векторная величина `vecp=q_1vecr_1+q_2vecr_2=q(vecr_2-vecr_1)=qvecl`, а величина `l=|vecl|=|vecr_2-vecr_1|` называется плечом диполя.

e/(4pi epsilon_0) (2Rl)/(R^4) =1/(4pi epsilon_0) (2el)/(R^3)=1/(4pi epsilon_0) (2p)/(R^3)

Рассмотрим более сложный пример использования принципа суперпозиции.

По тонкому кольцу радиусом `r` равномерно распределён заряд `q`. Найти напряжённость электрического поля на оси кольца в точке `A`, расположенной на расстоянии `R` от центра (рис. 7).

1/(4pi epsilon_0) q/(R^2)` для точечного заряда.

Электрическое поле бесконечной равномерно заряженной плоскости

Вычисление поля в данном случае требует привлечения знаний высшей математики. Без сложных вычислений можно, однако, сделать два следующих утверждения, основываясь лишь на соображениях симметрии, а также на том факте, что густота линий напряжённости пропорциональна величине `vecE` (см. Учебник):

1) Электрическое поле бесконечной равномерно заряженной плоскости перпендикулярно плоскости (рис. 8). Дело в том, что перпендикуляр к плоскости – единственное выделенное направление в задаче. Если бы вектор `vecE` был направлен под некоторым углом `alpha` к плоскости, мы бы ещё спросили себя: «Чем это направление лучше, чем все другие прямые, имеющие тот же угол `alpha` с плоскостью, и направленные вдоль образующих конуса с углом `alpha` при вершине?» Ясно, что ничем не лучше: если плоскость бесконечная и заряжена одинаково во всех точках, то и любые направления вдоль неё эквивалентны друг другу.

Величина вектора напряжённости `vecE` может быть вычислена по формуле

Хотя в природе не существует бесконечных равномерно заряженных плоскостей, формула (1.3.4) с успехом используется для расчётов электрических полей заряженных тел в виде больших пластин или просто плоских объектов при небольшом удалении от центральной их части.

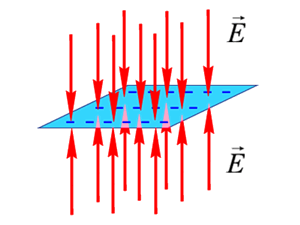
Электростатическое поле создаётся двумя бесконечными параллельными плоскостями, заряженными с поверхностными плотностями заряда `sigma_1=-1 «нКл»//»м»^2` и `sigma_2=+1 «нКл»//»м»^2`. Определить напряжённость электрического поля между плоскостями и снаружи.

`|sigma_1|=sigma_2-=sigma`, `|E_1|=|E_2|-=E=sigma//2 epsilon_0`. Далее воспользуемся принципом суперпозиции полей. Между плоскостями напряжённости полей отдельных пластин направлены в одну и ту же сторону (рис. 9), по этому результирующая напряжённость `E_(«in»)=2E=sigma//epsilon_0=113` В/м и направлена от положительной плоскости к отрицательной. Снаружи поля разных плоскостей направлены в противоположные стороны, поэтому результирующая напряжённость поля там `E_(ex)=0`.

Пользуясь принципом суперпозиции, доказать, что напряжённость электрического поля равномерно заряженной полусферической чаши во всех точках плоскости, стягивающей края чаши (как кожа на барабане), перпендикулярна этой плоскости.

Мысленно дополним полусферу ещё одной такой же полусферой так, чтобы получилась целая сфера. Напряжённость поля внутри равномерно заряженной сферы равна нулю. С другой стороны, эта напряжённость складывается из двух напряжённостей – исходной полусферы `vecE` и мысленно добавленной `vecE^’`. Таким образом, имеем равенство `vecE+vecE^’=0`, или `vecE=-vecE^’`. Последнее возможно только в том случае, если углы наклона векторов `vecE` и `vecE^’` к плоскости одинаковы, т. е. равны `90^@` (рис. 10).

Источник

Закон Кулона. Принцип суперпозиции. Теорема Гаусса. Потенциал. Проводник в электростатическом поле

Страницы работы

Содержание работы

Урок №1

Закон Кулона. Принцип суперпозиции. Теорема Гаусса.

Одно из фундаментальных взаимодействий – взаимодействие между электрическими зарядами.

Свойства электрического заряда:

1. Существует в двух видах: положительный и отрицательный.

2. В электрически изолированной системе суммарный заряд сохраняется.

3. Величина заряда инвариантна по отношению к инерциальным системам отсчета.

Два точечных покоящихся заряда в вакууме взаимодействуют с силой , где r – расстояние между зарядами.

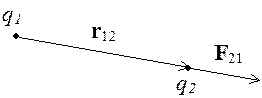
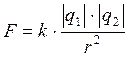
Сила направлена по прямой, соединяющей заряды, и является силой отталкивания, если заряды одноименные, и силой притяжения, если заряды разного знака.

– в системе СИ

– электрическая постоянная

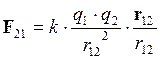
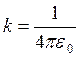
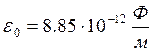
Законом Кулона можно воспользоваться и в том случае, если один из зарядов или оба заряда не являются точечными, но их распределение обладает сферической симметрией. В этом случае r – расстояние между центрами зарядов.

Взаимодействие между зарядами осуществляется через поле, которое создается зарядом в окружающем пространстве.

– напряженность поля, создаваемого зарядом q₁ в точке, определяемой радиус-вектором

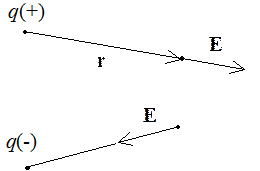
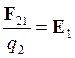
Отвлекаясь от индексов 1 и 2, .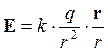

Таким образом, напряженность поля в некоторой точке – это сила, действующая на единичный положительный заряд, помещенный в данную точку поля.

Принцип суперпозиции: напряженность электрического поля в данной точке определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами в этой точке.

Если заряды распределены непрерывно, то

, где dq = t . dl, t – линейная плотность заряда, или

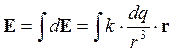
dq = s . dl, s – поверхностная плотность заряда, или

dq = r . dV, r – объемная плотность заряда.

Силу, действующую на произвольный заряд q, помещенный в точку поля, где напряженность Е, можно найти по формуле:

Силовыми линиями электрического поля называются воображаемые кривые, в каждой точке которых вектор Е направлен к ним по касательной. Величину поля Е договоримся определять густотой силовых линий, т.е. количеством силовых линий, пересекающих единичную площадку к ним перпендикулярную.

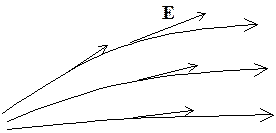
Потоком вектора Е через площадку dS называется:

Вектором площадки называется

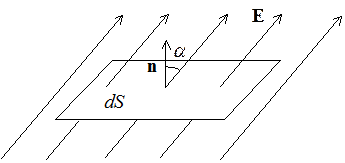
где n – единичный вектор нормали к данной площадке. Если площадка замкнутая, то в качестве положительной нормали всегда выбирается внешняя.

Поток вектора Е через произвольную площадку S определяется:

Оказывается, что поток вектора Е через замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на e₀:

Данное утверждение называют теоремой Гаусса.

Теорема Гаусса в дифференциальном виде:

, где

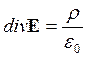
r – объемная плотность электрического заряда в той точке, где ищется .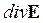

Примеры решения задач

Задача №1

Тонкое полукольцо радиусом 10 см равномерно заряжено с линейной плотностью заряда 1 мкКл/м. В центре кривизны полукольца находится точечный заряд 20 нКл. Найти силу взаимодействия точечного заряда и полукольца.

Поскольку заряженное полукольцо не является точечным зарядом, то его следует мысленно разбить на элементарные заряды dq = t . dl, где элемент дуги .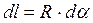

Сила взаимодействия dF между точечным зарядом q и элементарным зарядом кольца dq найдется по закону Кулона:

Результирующая сила F найдется векторной суммой всех dF, действующих на заряд q:

Из симметрии задачи можно понять, что результирующая сила F направлена вертикально вниз. Выберем в этом направлении ось y, тогда для величины силы F:

Задача №2

По тонкому кольцу радиуса 10 см равномерно распределен заряд 2 мкКл. Найти максимальную силу, действующую на точечный заряд 1 мкКл, находящийся на оси кольца.

Рассчитаем силу, действующую на заряд q₂, по формуле

, где E – напряженность поля, создаваемого кольцом.

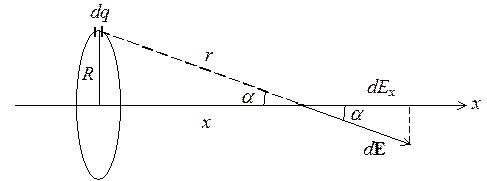
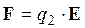
Вычислим 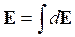по принципу суперпозиции. Мысленно разобьем кольцо на элементарные заряды dq, которые создают на оси кольца поле

Из симметрии задачи следует, что результирующий вектор E будет направлен по оси х, поэтому

Суммирование всех элементарных зарядов по кольцу даст нам суммарный заряд кольца:

Чтобы найти максимальную силу, нужно определить расстояние х (от центра кольца до точки расположения заряда q₂), при котором функция F(x) имеет максимум:

В двух точках на оси, расположенных слева и справа от плоскости кольца на расстоянии 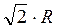от его центра, сила будет максимальной:

Задача №3

Две длинные прямые параллельные нити, заряженные равномерно с линейной плотностью 20 нКл/м, находятся на расстоянии 10 см. Найти напряженность поля в точке, лежащей на расстоянии 10 см от обеих нитей.

Поле E найдем по принципу суперпозиции, как сумму полей двух нитей: .

Поле бесконечной нити на расстоянии «а» от нее найдем, используя теорему Гаусса. Из соображений симметрии задачи следует, что силовыми линиями являются радиально расходящиеся прямые, лежащие в плоскости, перпендикулярной нити.

Источник