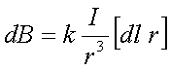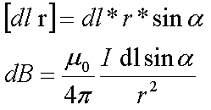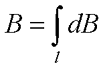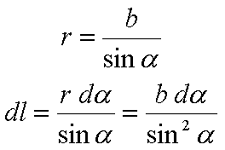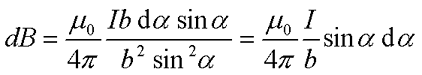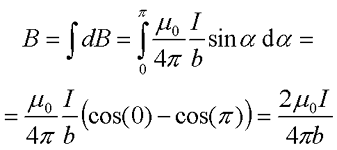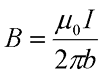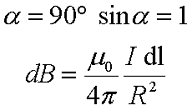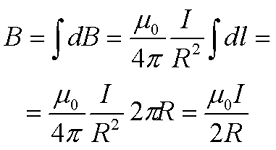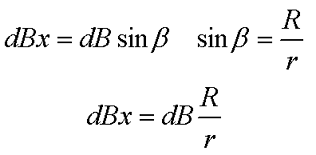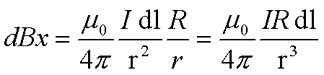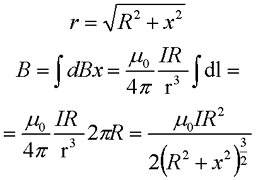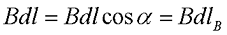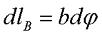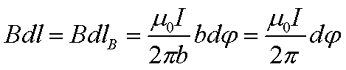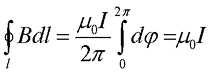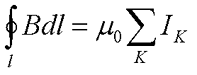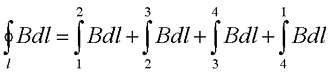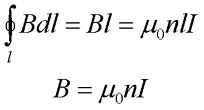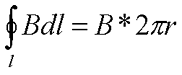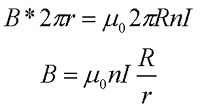поле кольца с током

Учебники

Журнал «Квант»

Общие

§12. Постоянное магнитное поле

12.7 Расчет индукции магнитного поля.

Закон Био-Саварра-Лапласа и принцип суперпозиции позволяют рассчитать индукцию магнитного поля \(

I \Delta \vec l\) записывается также в виде \(

I \Delta \vec l\) следует заменить эквивалентным \(

\vec j \Delta V\) и провести суммирование по всем элементам объема., где протекают электрические токи.

Конечно, такое суммирование часто представляет собой громоздкую математическую задачу (в конце концов, для его выполнения можно воспользоваться компьютером), но, с физической точки зрения, изложенный метод дает полное решение задачи.

Рассмотрим несколько примеров расчета индукции магнитного поля по изложенной выше методике.

12.7.1 Магнитное поле кругового тока.

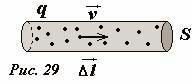
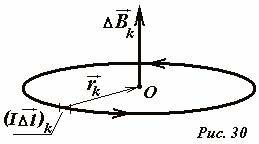
Пусть постоянный электрический ток силой I протекает по плоскому круглому контуру радиуса R. Найдем индукцию поля в центре кольца в точке O (Рис. 30). Мысленно разобьем кольцо на малые участки, которые можно считать прямолинейными, и применим закон Био-Саварра-Лапласа для определения индукции поля, создаваемого этим элементом, в центре кольца. В данном случае вектор элемента тока \(

(I \Delta \vec l)_k\) и вектор \(

Для любого другого элемента кольца ситуация абсолютно аналогична – вектор индукции также направлен по оси кольца, а его модуль определяется формулой (1). Поэтому суммирование этих векторов выполняется элементарно и сводится к суммированию длин участков кольца

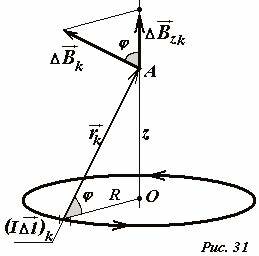
(I \Delta \vec l)_k\) и строим вектор индукции поля \(

(\Delta \vec B)_k\) и осью кольца. Запишем выражение для модуля искомого суммарного вектора индукции

Из рисунка следует, что \(

Как и следовало ожидать, в центре кольца (при z = 0) формула (3) переходит в полученную ранее формулу (2).

Задания для самостоятельной работы.

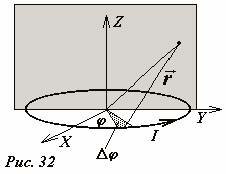
Используя общий рассматриваемый здесь метод, можно рассчитать индукцию поля в произвольной точке. Рассматриваемая система обладает осевой симметрией, поэтому достаточно найти распределение поля в плоскости, перпендикулярной плоскости кольца и проходящей через его центр. Пусть кольцо лежит в плоскости xOy (рис.32), а поле рассчитывается в плоскости yOz. Кольцо следует разбить на малые участки, видимые из центра под углом Δφ и просуммировать поля создаваемые этими участками. Можно показать (попробуйте проделать это самостоятельно), что компоненты вектора магнитной индукции поля, создаваемого одним выделенным элементом тока, в точке с координатами (y,z) рассчитываются по формулам:

Необходимое суммирование не может быть проведено аналитически, так как при переходе от одного участка кольца к другому изменяются расстояния до точки суммирования. Поэтому «простейший» способ провести такое суммирование – использовать компьютер.

Если же известно значение вектора индукции (или хотя бы имеется алгоритм его расчета) в каждой точке, то можно построить картину силовых линий магнитного поля. Очевидно, что алгоритм построения силовых линий векторного поля не зависит от его физического содержания, а такой алгоритм был кратко рассмотрен нами при изучении электростатики.

На рис. 33 картина силовых линий рассчитана при разбиении кольца на 20 частей, этого оказалось вполне достаточно, так как и при 10 интервалах разбиения получался практически тот же рисунок.

Рассмотрим выражение для индукции поля на оси кольца на расстояниях значительно больших радиуса кольца z >> R. В этом случае формула (3) упрощается и приобретает вид

Такое совпадение не случайно, более того, можно показать, что подобное соответствие справедливо для любой точки поля, находящейся на больших расстояниях от кольца. Фактически малый контур с током является магнитным диполем (два одинаковых малых противоположно направленных элемента тока) – поэтому его поле совпадает с полем электрического диполя. Чтобы ярче подчеркнуть этот факт, на рис. 34 приведена картина силовых линий магнитного поля кольца, на больших расстояниях от него (сравните с аналогичной картиной для поля электрического диполя).

12.7.2 Магнитное поле прямого тока.

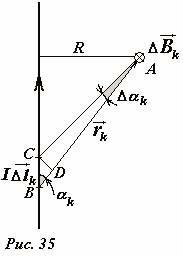
Рассчитаем индукцию магнитного поля, создаваемого бесконечным [1] проводником, по которому протекает электрический ток силой I (Рис. 35) Методика расчет остается прежней: мысленно разбиваем проводник на малые участки \(

I \Delta \vec l_k\). Согласно закона Био-Саварра-Лапласа в произвольной точке A, находящейся на расстоянии R от проводника, произвольный элемент тока создает магнитное поле, вектор индукции которого \(

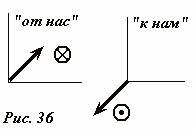
Договоримся об еще одном общепринятом соглашении. Достаточно часто приходится изображать векторы, перпендикулярные плоскости рисунка. В этом случае эти векторы изображаются в виде (рис. 36): небольшого кружка с точкой в центре, если вектор направлен «на нас» (видно «острие» вектора); кружка с перекрестием, если вектор направлен от нас (видно «оперение» вектора).

Векторы поле, созданных всеми другими участками проводника, направлены также, поэтому суммирование векторов в данном случае сводится к суммированию их модулей. Но даже вычислить сумму модулей не просто, так как для различных участков проводника расстояния r_k и α_k различны. Тем не менее, такое суммирование выполнимо, его результат выражается формулой, определяющей величину индукции магнитного поля бесконечного прямого тока

здесь не приведено вычисление последней суммы (которая равна \(

\sum_k \frac<\Delta l_k> \sin \alpha_k = \frac<2>\)), поверьте пока в справедливость полученного выражения, хотя бы потому, что оно имеет богатый физический смысл. Во-первых, эта формула совпадает с выражением для напряженности электрического поля, создаваемого бесконечной прямой равномерно заряженной нитью; во-вторых, оно соответствует результату опытов А.М. Ампера по изучению взаимодействия параллельных токов. Действительно, если один проводник создает магнитное поле, индукция которого обратно пропорциональна расстоянию до проводника, то на второй проводник действует сила Ампера, пропорциональная индукции поля, то есть обратно пропорциональная расстоянию между проводниками.

Дадим теперь строгий вывод формулы для суммы, фигурирующей в выражении (2). Проще всего она выводится с помощью операции интегрирования, но здесь мы дадим ее геометрический вывод. Для начала с помощью рис. 35 преобразуем каждое слагаемое этой формулы \(

\Delta l_k \sin \alpha_k\) равно длине отрезка CD, перпендикулярного вектору \(

\frac<\Delta l_k> \sin \alpha_k = \frac<|CD|> = \Delta \alpha_k\) (3)

( точнее, это отношение равно тангенсу угла, который для малых углов равен самому углу, измеренному в радианах). Из того же рисунка следует, что отношение \(

\frac <\sin \alpha_k>= R\) равно расстоянию от точки наблюдения до проводника и не зависит от выбора участка проводника. С учетом этого соотношения и формулы (2) получим

Таким образом, вычисление суммы (2) сводится к вычислению суммы \(

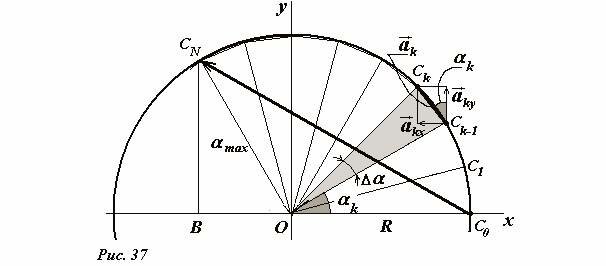
Для вычисления этой суммы применим искусственный прием (он встретится нам и в дальнейшем). Возьмем окружность (Рис. 37) радиуса R и разобьем ее точками C₀, C₁, C₂, …, C_N на малые участки, угловой размер каждого равен Δα.

Хорды, которые образованы точками разбиения будем рассматривать как векторы \(

Теперь, внимание, если справедливо векторное равенство, то справедливо аналогичное выражение для любой проекции этих векторов. Введем декартовую систему координат с началом в центре окружности, ось Ox которой проходит через начальную точку. Длины построенных вписанных векторов равны \(

|\vec a_k| = R \Delta \alpha_k\) (точнее, это длина дуги, но для малых углов, длина стягивающей хорды стремится к длине дуги). Из рисунка 37 следует, что проекции этого вектора на оси координат равны, соответственно,

Проецируя равенство (4) на оси координат получим

Проекции суммарного вектора \(

\vec A\) на оси координат находятся просто

Сравнивая выражения (5) и (6) получим искомые формулы

Еще раз подчеркнем, что суммирование в этих формулах проводится в пределах изменения угла от нуля до предельного значения α_max.

Осталось принять во внимание, что бесконечный прямой проводник виден из любой точки вне его под углом α_max = π, поэтому искомая сумма выражается формулой

что и требовалось доказать.

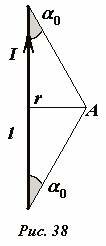
Оценим длину «бесконечного» в данном случае проводника – во сколько раз длина проводника должна быть больше расстояния до точки наблюдения, что бы погрешность расчета индукции поля по формуле (2), примененной к проводнику конечной длины, была пренебрежимо малой.

Пусть длина прямого проводника равна l, а индукция поля рассчитывается в точке A, находящейся на расстоянии r (считаем, что r [2]

Такая ошибка будет допущена, если отношение длины проводника к расстоянию до точки наблюдения равно \(

\frac = \frac<2><\varepsilon>\). Так для относительной ошибки ε = 1% искомое отношение равно \(

\frac \approx 15\). Итак, в рассмотренном случае «бесконечность» равна 15.

Примечания

(1 + x)^\beta \approx 1 + \beta x\) (в данном случае \(\beta = \frac<1><2>\)).

Источник

ElectronicsBlog

Обучающие статьи по электронике

Магнитная индукция в вакууме

Всем доброго времени суток. В прошлой статье я рассказал о магнитном поле и немного остановился на его параметрах. Данная статья продолжает тему магнитного поля и посвящена такому параметру как магнитная индукция. Для упрощения темы я буду рассказывать о магнитном поле в вакууме, так как различные вещества имеют разные магнитные свойства, и как следствие необходимо учитывать их свойства.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Закон Био – Савара – Лапласа

В результате исследования магнитных полей создаваемых электрическим током, исследователи пришли к таким выводам:

Французские учёные Био и Савар, которые пришли к таким выводам обратились к великому математику П. Лапласу для обобщения и вывода основного закона магнитной индукции. Он высказал гипотезу, что индукция в любой точке магнитного поля, создаваемое проводником с током можно представить в виде суммы магнитных индукций элементарных магнитных полей, которые создаются элементарным участком проводника с током. Данная гипотеза и стала законом магнитной индукции, называемого законом Био – Савара – Лапласа. Для рассмотрения данного закона изобразим проводник с током и создаваемую им магнитную индукцию

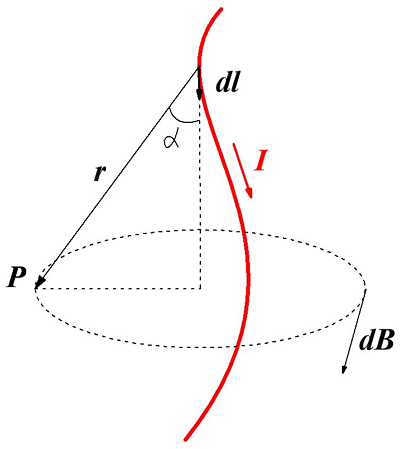
Магнитная индукция dB, создаваемая элементарным участком проводника dl.

Тогда магнитная индукция dB элементарного магнитного поля, которое создается участком проводника dl, с током I в произвольной точке Р будет определяться следующим выражением

где I – сила тока, протекающая по проводнику,

r – радиус-вектор, проведённый от элемента проводника к точке магнитного поля,

dl – минимальный элемент проводника, который создает индукцию dB,

k – коэффициент пропорциональности, зависящий от системы отсчёта, в СИ k = μ₀/(4π)

Так как [dl r] является векторным произведением, тогда итоговое выражение для элементарной магнитной индукции будет выглядеть следующим образом

Таким образом, данное выражение позволяет найти магнитную индукцию магнитного поля, которое создается проводником с током произвольной формы и размеров при помощи интегрирования правой части выражения

где символ l обозначает, что интегрирование происходит по всей длине проводника.

Магнитная индукция прямолинейного проводника

Как известно простейшее магнитное поле создает прямолинейный проводник, по которому протекает электрический ток. Как я уже говорил в предыдущей статье, силовые линии данного магнитного поля представляют собой концентрические окружности расположенные вокруг проводника.

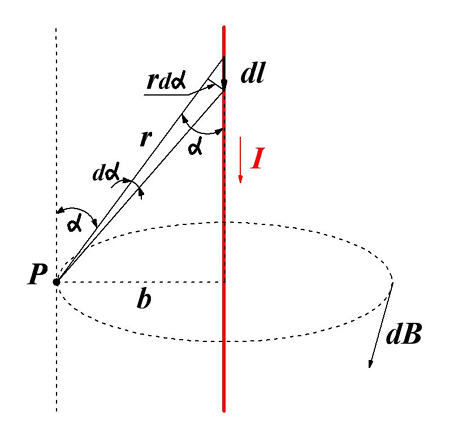
Магнитная индукция магнитного поля создаваемого прямолинейным проводником с током.

Для определения магнитной индукции В прямого провода в точке Р введем некоторые обозначения. Так как точка Р находится на расстоянии b от провода, то расстояние от любой точки провода до точки Р определяется как r = b/sinα. Тогда наименьшую длину проводника dl можно вычислить из следующего выражения

В итоге закон Био – Савара – Лапласа для прямолинейного провода бесконечной длины будет иметь вид

где I – ток, протекающий по проводу,

b – расстояние от центра провода до точки, в которой рассчитывается магнитная индукция.

Теперь просто проинтегрируем получившееся выражение по dα в пределах от 0 до π.

Таким образом, итоговое выражение для магнитной индукции прямолинейного провода бесконечной длины будет иметь вид

I – ток, протекающий по проводу,

b – расстояние от центра проводника до точки, в которой измеряется индукция.

Магнитная индукция кольца

Индукция прямого провода имеет небольшое значение и уменьшается при удалении от проводника, поэтому в практических устройствах практически не применяется. Наиболее широко используются магнитные поля созданные проводом, намотанным на какой либо каркас. Поэтому такие поля называются магнитными полями кругового тока. Простейшим таким магнитным поле обладает электрический ток, протекающий по проводнику, который имеет форму окружности радиуса R.

В данном случае практический интерес представляет два случая: магнитное поле в центре окружности и магнитное поле в точке Р, которое лежит на оси окружности. Рассмотрим первый случай.

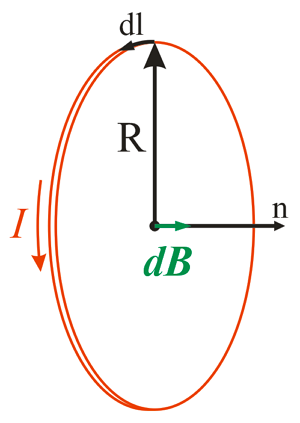
Магнитная индукция в центре кругового тока.

В данном случае каждый элемент тока dl создаёт в центре окружности элементарную магнитную индукцию dB, которая перпендикулярна к плоскости контура, тогда закон Био-Савара-Лапласа будет иметь вид

Остается только проинтегрировать полученное выражение по всей длине окружности

I – сила тока в проводнике,

R – радиус окружности, в которое свернут проводник.

Рассмотрим второй случай, когда точка, в которой вычисляется магнитная индукция, лежит на прямой х, которая перпендикулярна плоскости ограниченной круговым током.

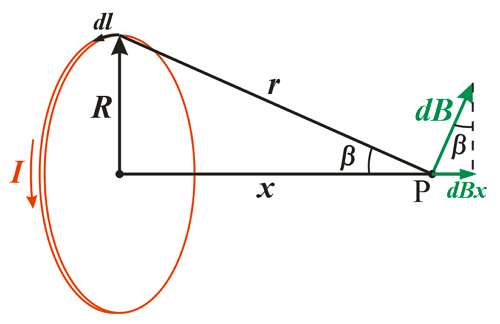
Магнитная индукция в точке, лежащей на оси окружности.

В данном случае индукция в точке Р будет представлять собой сумму элементарных индукций dB_X, которые в свою очередь представляет собой проекцию на ось х элементарной индукции dB

Применив закон Био-Савара-Лапласа вычислим величину магнитной индукции

Теперь проинтегрируем данное выражение по всей длине окружности

I – сила тока в проводнике,

R – радиус окружности, в которое свернут проводник,

х – расстояние от точки, в которой вычисляется магнитная индукция, до центра окружности.

Как видно из формулы при х = 0, получившееся выражение переходит в формулу для магнитной индукции в центре кругового тока.

Циркуляция вектора магнитной индукции

Для расчёта магнитной индукции простых магнитных полей достаточно закона Био-Савара-Лапласа. Однако при более сложных магнитных полях, например, магнитное поле соленоида или тороида, количество расчётов и громоздкость формул значительно увеличится. Для упрощения расчётов вводится понятие циркуляции вектора магнитной индукции.

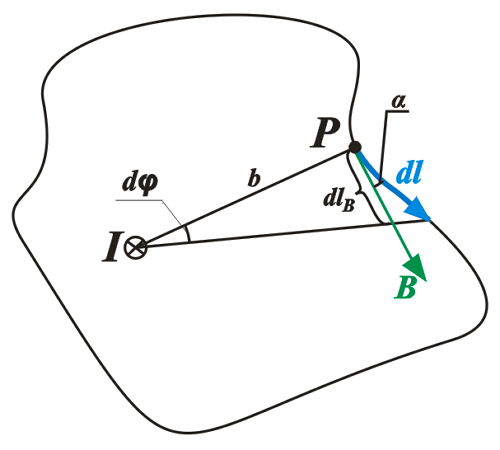
Циркуляция вектора магнитной индукции по произвольному контуру.

Представим некоторый контур l, который перпендикулярный току I. В любой точке Р данного контура, магнитная индукция В направлена по касательной к данному контуру. Тогда произведение векторов dl и В описывается следующим выражением

Так как угол dφ достаточно мал, то векторов dl_В определяется, как длина дуги

Таким образом, зная магнитную индукцию прямолинейного проводника в данной точке, можно вывести выражение для циркуляции вектора магнитной индукции

Теперь остаётся проинтегрировать получившееся выражение по всей длине контура

В нашем случае вектор магнитной индукции циркулирует вокруг одного тока, в случае же нескольких токов выражение циркуляции магнитной индукции переходит в закон полного тока, который гласит:

Циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, которые охватывает данный контур.

Магнитное поле соленоида и тороида

С помощью закона полного тока и циркуляции вектора магнитной индукции достаточно легко определить магнитную индукцию таких сложных магнитных полей как у соленоида и тороида.

Соленоидом называется цилиндрическая катушка, которая состоит из множества витков проводника, намотанных виток к витку на цилиндрический каркас. Магнитное поле соленоида фактически состоит из множества магнитных полей кругового тока с общей осью, перпендикулярной к плоскости каждого кругового тока.

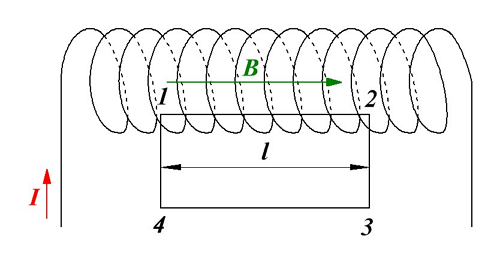
Магнитная индукция соленоида.

Воспользуемся циркуляцией вектора магнитной индукции и представим циркуляцию по прямоугольному контуру 1-2-3-4. Тогда циркуляция вектора магнитной индукции для данного контура будет иметь вид

Так как на участках 2-3 и 4-1 вектор магнитной индукции перпендикулярен к контуру, то циркуляция равна нулю. На участке 3-4, который значительно удалён от соленоида, то его так же можно не учитывать. Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид

где n – число витков проводника соленоида, которое приходится на единицу длины,

I – ток, протекающий по соленоиду.

Тороид образуется путём намотки проводника на кольцевой каркас. Данная конструкция эквивалентна системе из множества одинаковых круговых токов, центры которых расположены на окружности.

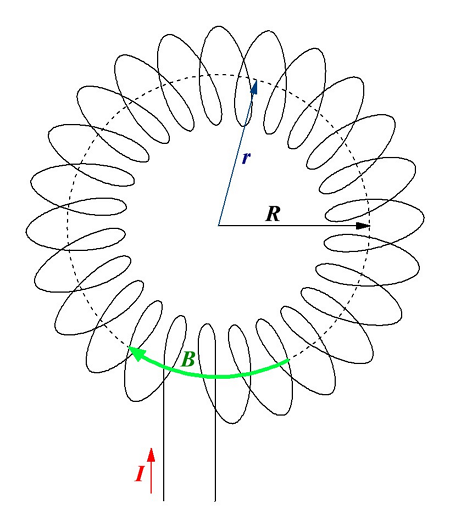
Магнитная индукция тороида.

В качестве примера рассмотрим тороид радиуса R, на который намотано N витков провода. Вокруг каждого витка провода возьмём контур радиуса r, центр данного контура совпадает в центром тороида. Так как вектор магнитной индукции B направлен по касательной к контуру в каждой точке контура, то циркуляция вектора магнитной индукции будет иметь вид

где r – радиус контура магнитной индукции.

Контур проходя внутри тороида охватывает N витков провода с током I, тогда закон полного тока для тороида будет иметь вид

где n – число витков проводника, которое приходится на единицу длины,

r – радиус контура магнитной индукции,

Таким образом, используя закон полного тока и циркуляцию вектора магнитной индукции можно рассчитать сколь угодно сложное магнитное поле. Однако закон полного тока дает правильные результаты только лишь в вакууме. В случае расчёта магнитной индукции в веществе необходимо учитывать так называемые молекулярные токи. Об этом пойдёт речь в следующей статье.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник

Магнитное поле кругового тока

Вы будете перенаправлены на Автор24

Французские ученые Ж. Био и Ф. Савар изучали магнитные поля, создаваемые постоянными токами разной формы. Результаты их работы обобщил известный математик и физик П. Лаплас.

Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока

Магнитные поля подчиняются принципу суперпозиции:

Суммарную магнитную индукцию поля, создаваемого несколькими источниками, находят как геометрическую сумму векторов магнитной индукции отдельных полей:

Если распределение токов можно считать непрерывным, то принцип суперпозиции можно записать:

Вычисление магнитной индукции поля с применением закона Био-Савара-Лапласа довольно сложная процедура. Но при существовании определенной симметрии в распределении токов, используя, рассмотренный нами закон и принцип суперпозиции, рассчитать конкретные поля просто. В любом случае следует придерживаться следующей схемы действий:

Готовые работы на аналогичную тему

Магнитное поле кругового тока в его центре

Рисунок 1. Магнитное поле кругового тока в его центре. Автор24 — интернет-биржа студенческих работ

Запишем закон Био-Савара-Лапласа для модуля вектора индукции поля, создаваемого элементом d$l_1$:

Учитывая сказанное выражение (5) представим в виде:

Поскольку наш ток является непрерывным, то для нахождения полного поля в его центре, мы проинтегрируем (6), имеем:

Индукция магнитного поля кругового тока на его оси

Рисунок 2. Индукция магнитного поля кругового тока на его оси. Автор24 — интернет-биржа студенческих работ

Как основу для выполнения поставленной задачи возьмем закон Био-Савара-Лапласа (1), где из рис.2 мы видим, что:

$d\vec\times \vec=d\vec\times \vec+d\vec\times \vec(9).$

Используя принцип суперпозиции закон (1) для нашего тока и формулы (8-9) запишем:

$\oint\limits_L \times \vec> =(\oint\limits_L )\times\vec> =0\, \left( 11 \right),$

$\oint\limits_L \times \vec=\oint\limits_L <\vecRdl=\vecR>> \oint\limits_LR> 2\pi R=2\pi R^<2>\vec\left( 12 \right)$.

Подставляем результаты интегрирования из (12) в (10), имеем:

где при записи окончательного результата мы учли, что:

Кольца Гельмгольца

Кольцами Гельмгольца считают пару проводников в виде колец одного радиуса, расположенных в параллельных плоскостях (рис.3) на одной оси. Расстояние между плоскостями колец равно их радиусу.

Рисунок 3. Кольца Гельмгольца. Автор24 — интернет-биржа студенческих работ

Рассмотрим магнитное поле на оси этих колец.

Декартову систему координат разместим так, что ее начало совпадает с центром нижнего кольца с током. Ось Z нашей системы будет направлена по оси колец (рис.3).

Исследуем полученное поле. Считается, что магнитное поле на оси колец Гельмгольца на посередине между ними является однородным.

Неоднородность в первом приближении характеризуют первой производной:

На середине их общей оси ($z=\frac<2>)$, получаем:

Источник